最短路径(二)—Dijkstra算法(通过边实现松弛:邻接矩阵)
上一节通过Floyd-Warshall算法写了多源节点最短路径问题:
http://blog.csdn.net/wtyvhreal/article/details/43315705
这一节来学习指定一个点(源点)到其余各个顶点的最短路径。也叫做“单源最短路径”Dijkstra。
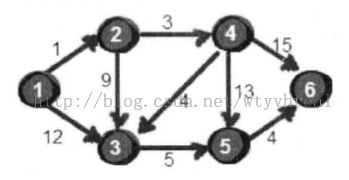
例如求下图中1号顶点到2、3、4、5、6号顶点的最短路径。
用二维数组e存储顶点之间边的关系,初始值如下:
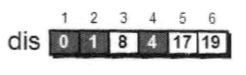
用一个一维数组dis来存储1号顶点到其余各个顶点的初始路程,
此时dis数组中的值称为最短路程的“估计值”。
先找一个离1号顶点最近的顶点,是2号顶点,当选择了2号顶点后,dis[2]的值就已经 从“估计值”变为了“确定值”。接下来看2号顶点的出边,有2-3和2-4两条边。先讨论通过2-3能否让1-3号的路程变短,也就是比较dis[3]和dis[2]+e[2][3]的大小。2-4同理。
我们对2号顶点所有出边进行了松弛,完毕后dis数组为:
接下来,继续在剩下的3、4、5、6顶点中,选注离1号最近的顶点,是4号,4号的所有出边4-3、4-5、4-6松弛:
。。。
Dijkstra的主要思想:每次找到离源点最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其余所有点的最短路径。
步骤:
输入数据:
运行结果:
![]()
这个时间复杂度是O(N^2)。
其中每次找到离1号顶点最近的顶点的时间复杂度是O(N),这里可以用“堆”来优化使降低到O(logN),
另外对于边数M少于N^2的稀疏图来说(M<<N^2的图称为稀疏图,而M较大的图称为稠密图),我们可以用邻接表来代替邻接矩阵存储,使得整个时间复杂度优化到O(M+N)logN。
在最坏的情况下M就是N^2,这样的话(M+N)logN要比N^2还要大,但是大多数情况下并不会有那么多边,因此(M+N)logN要比N^2小很多。
DijkStra基于贪心策略的算法。
对于不含负权边的图求单源最短路径,Dijkstra算法是最高效的。但是在含负权边的图中,Dijkstra很可能得不到正确的结果,因为Dijkstra每次选的是当前能连到的边中权值最小的,在正权图中这种贪心是对的,但是在负权图中就不是这样了。比如1——>2权值为5,1——>3权值为6,3——>2权值为-2,求1到2的最短路径时,Dijkstra就会选择权为5的1——>2,但实际上1——>3——>2才是最优的结果。
另外如果包含负环,则意味着最短路径不存在。因为只要在负权回路上不断兜圈子,所得的最短路长度可以任意小。
原因:
Dijkstra算法当中将节点分为已求得最短路径的集合(记为P)和未确定最短路径的集合(记为Q),归入P集合的节点的最短路径及其长度不再变更,如果边上的权值允许为负值,那么有可能出现当与P内某点(记为a)以负边相连的点(记为b)确定其最短路径时,它的最短路径长度加上这条负边的权值结果小于a原先确定的最短路径长度,而此时a在Dijkstra算法下是无法更新的,由此便可能得不到正确的结果。