/*
TreeArray.h
树状数组,一维和二维都有。数组必须从1开始
问题:
已知数组a[],元素个数为n,现在更改a中的元素,要求得新的a数组中i到j区间内的和
解决方法:
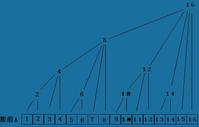
从图中不难发现,c[k]存储的实际上是从k开始向前数k的二进制表示中右边第一个1所代表的数字
个元素的和(这么说可能有点拗口,令lowbit为k的二进制表示中右边第一个1所代表的数字,然后
c[k]里存的就是从a[k]开始向前数lowbit个元素之和)
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
这么存的好处:
无论是树状数组还是线段树,都用到了分块的思想
方便计算,我们可以用位运算轻松地算出lowbit.
时间复杂度:
对于更改元素来说,如果第i个元素被修改了,可以直接在c数组里面进行相应的更改,如图中的例子,
假设更改的元素是a[2],那么它影响到得c数组中的元素只有c[2],c[4],c[8],我们只需一层一层往
上修改就可以了,这个过程的最坏的复杂度也不过O(logN);
对于查找来说,如查找s[k],只需查找k的二进制表示中1的个数次就能得到最终结果,比如查找s[7],7的二进制表示中有3个1,也就是要查
找3次,到底是不是呢,我们来看上图,s[7]=c[7]+c[6]+c[4]
怎么实现这个过程:
还以7为例,二进制为0111,右边第一个1出现在第0位上,也就是说要从a[7]开始向前数1个元素(只
有a[7]),即c[7];
然后将这个1舍掉,得到6,二进制表示为0110,右边第一个1出现在第1位上,也就是说要从a[6]开始
向前数2个元素(a[6],a[5]),即c[6];
然后舍掉用过的1,得到4,二进制表示为0100,右边第一个1出现在第2位上,也就是说要从a[4]开始
向前数4个元素(a[4],a[3],a[2],a[1]),即c[4].
*/
#include<iostream>
using namespace std;
#define MAX 1002
class TreeArray
{
public:
int **s;
int type;
public:
TreeArray(int t);
~TreeArray();
void clear();
int lowbit(int x){return x&(-x);};
void modify(int x, int value);
void modify(int x, int y, int value);
int sum(int x);
int sum(int x, int y);
};
TreeArray::TreeArray(int t):type(t)
{
int i;
s = new int*[MAX+1];
//一维
if(type == 1)
{
for(i = 0; i <= MAX; i++)
s[i] = new int;
}
//二维
else if(type == 2)
{
for(i = 0; i <= MAX; i++)
s[i] = new int[MAX+1];
}
}
TreeArray::~TreeArray()
{
int i;
for(i = 0; i <= MAX; i++)
delete []s[i];
delete []s;
}
void TreeArray::clear()
{
int i, j;
for(i = 0; i <= MAX; i++)
{
if(type == 1)
s[i][0] = 0;
else
{
for(j = 0; j <= MAX; j++)
s[i][j] = 0;
}
}
}
void TreeArray::modify(int x, int value)
{
while(x <= MAX)
{
s[x][0] += value;
x += lowbit(x);
}
}
void TreeArray::modify(int x,int y,int value)
{
int temp = y;
while(x <= MAX)
{
y = temp;
while(y <= MAX)
{
s[x][y] += value;
y = y + lowbit(y);
}
x = x + lowbit(x);
}
}
int TreeArray::sum(int x)
{
int ans=0;
while(x > 0)
{
ans += s[x][0];
x -= lowbit(x);
}
return ans;
}
int TreeArray::sum(int x,int y)
{
int ans=0, temp = y;
while(x > 0)
{
y = temp;
while(y > 0)
{
ans += s[x][y];
y = y - lowbit(y);
}
x = x - lowbit(x);
}
return ans;
}
