<<什么是数学>> 余数那些事儿
<<什么是数学>> 笔记 余数那些事儿
今天又踩坑了,感觉各种问题递归下去有没个尽头的样子╮(╯_╰)╭
还是要回归到数学的本质上来...
只要说数学,你就会被高斯帅哭的...
一般性的概念.
只要碰到用一个固定的整数d,去除整数的问题,"同余"的概念和记法(高斯创造)使得这个推理简单而清楚.
(伟大的人都是把复杂的问题简单化)
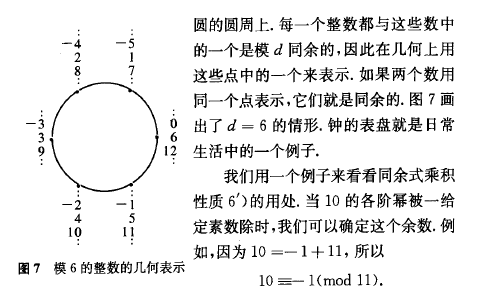
啊哈, 看图,"同余"的概念就很直观了.我们看到任意一个整数被5除时,剩下的余数是0,1,2,3,4,这五个数中的一个.如果两个整数a和b被5除有相同的余数,我们称它们是模5同余
同余数的表示方法,这就是同余式
一下命题等价:
1. a和b是模5同余.
2. 存在某个整数n, a = b + nd;
3. d 整除 a - b
一开始我很狐疑(我智商低求不鄙视..),为嘛 a = b + nd 会成立,如果a ,b 同余的话.
好,我们来证明一下
对于命题"如果 a,b 同余,那么 a = b + nd" 的证明:
假设a ,b 同余的话,可以假设它们对于模d的共同余数为为r.
那么有a = r + x*d;
b = r + y*d;
两个等式做减法. a - b = (x - y) * d; 变形 a = b + (x- y)*d.看,是不是如果用n表示 x - y 就能得到命题的证明了!
高斯的这种同余数表示方法之所以很方便,是因为它表示的同余式满足很多基础性的运算符法则,加,减,乘
这里的 加 减 乘 是针对 两对同余数(即同余式)来说的,而不是一对同余数 (不是天才就慢慢的思考嘛~,会有更深刻的认识)
证明一下:
已知, a == a' (mod d) , b == b'(mod d)
a = r + d*x;
a' = r + d*y;
b = p + d*m;
b' = p + d*n;
由于:
a + b = (r + p) + d*(x + m)
a' + b' = (r + p) + d*(y + n)
那么我们可以知道,a+b与a'+b'同余!
同理可以证明 5) 和 6)
大名鼎鼎的GCD算法的证明:
下面是我以前写的关于GCD的实现
http://blog.csdn.net/cinmyheart/article/details/39370553
证明过程简直beautiful,有木有! 超帅~
我今天终于明白...GCD为什么那样写了...
一条很重要的规律: 当a或b任意一个素数d的倍数时,那么他们的乘积也是d的倍数.这里重点其实在强调d必须是素数.
当d不是个素数的时候, 上述约束就不一定成立.
费马定理:
注意!p是个素数, 而且还是不能整除a的素数.
2^2 = 1 (mod 3)
2^4 = 1 (mod 5)
这样应该比较有感觉.
费马定理的证明:
对于"m1 m2 m3 ... mp-1 如果将其次序重新排序,必须相应的同余于数1 2 3 4 ... p-1"
这里要特别感谢 @青丝成霜
这里两个序列(m1 m2 ... mp-1) (1 2 3... p-1)他们其实是一组同余数组(同余系).
因为在m1 ... mp-1之间有 p-1个数, 而 这些数中任意两个都不能模p同余, 于是就有p-1种不同的余数结果.
而我们知道模p操作得到的余数可能情况全部就是p-1个, 这里恰好是所有的余数结果的.
就很容易知道, m1 .. mp-1 这些数模p得到的余数序列包含所有的余数情况. 进而这些余数都在0 ~ (p-1)之间.
所以就有了那句话"m1 m2 m3 ... mp-1 如果将其次序重新排序,必须相应的同余于数1 2 3 4 ... p-1"
后面其他余数相关的东东应该还会update~
update 2015.04.30 感谢@青丝成霜 的提醒. 对原文费马定理的证明进行了补充说明.