POJ3154 Graveyard（和刘汝佳的算法不一样哦）

原题地址在此 ： http://poj.org/problem?id=3154

      题目大意是原先一个圈上有n个分布均匀（连接后形成一个正多边形）的点，现在呢，要引入m个点，且引入后希望总的n+m个点形成一个正多边形，新来的点可以放在任意位置，但旧的点要在圆环上移动，现在希望你找出一个方案，使所有旧点总的移动距离最小。

      //写完之后发现好啰嗦啊，但不知道怎么说明，也罢也罢，以后有空再改。

      这道题是刘汝佳大白上看到的，觉得正常人的思维很容易想出那个算法，但是不容易证明正确性。某日我夜不能寐，终于纠结出了证明方法，紧接着就有了一个和书上不一样的算法，然后请注意，我这道题分的类是数论。

      先上代码，后写结论

# include <cstdio>

int min(int x,int y){return x<y?x:y;}
int gcd(int m, int n)
{
    return n? gcd(n,m%n) : m;
}
int main()
{
    int n,m;
	while (~scanf("%d%d",&n,&m))
	{
		int tmp = gcd(n,m);
		n /= tmp,m /= tmp;
	    int ans = 0;
		for (int i=0;i<n;i++)
			ans += min(i,n-i);
		printf("%.4f\n",(double)ans/(n*(n+m))*10000);
	}
    return 0;
}

然后是我的证明思路，证明这个算法需要证明两个结论：

      结论一：无论新的方案和旧的方案的相对位置是什么样的，对于原先的n个点来说，最好的策略就是往最近的新点位置上走。

      这个结论唯一一个需要想一下的地方是，两个旧点会不会站到一个坑里去。可以证明这是不会的，设旧的方案两个点之间距离为L，新的方案两个点之间距离为X,若两个旧点A，B跑到了同一个新点O上,就说明，|AO| < x/2 && |AB| < x/2 ，则L = |AB| <= |AO| + |BO| < 2*(X/2)  = X ,但事实上，L  > X。反正就是不会碰在一起。

      结论二：在结论一的前提下，有至少一个点重合的方案是最佳方案。

      这就是那个我“夜不能寐”证出来的结论。首先，一开始是n个点，后来是n+m个点，就是说一开始间隔是1/n,后来是1/(n+m)。为了但是用分数看实在不方便，我们取1/（n*(n+m)）为基本单位，这样，旧的间隔是n+m，后来的间隔是n。在这里请假设n与n+m互质，如果不是互质，我们就进行约分，原因后来会知道。

      然后，我们先假设有新的方案和旧的方案有一个点是重合的，其中红色的线段和点是旧的方案，蓝色的是新的方案；

      然后我们沿着这个重合的点，将圆环剪开，注意首尾相同，颜色没有变哦。

    

      你有看出什么东西吗？好吧，如果没有，那么请你看下一步，将AB‘，B’D , DC'，C'A线段（即所有的蓝色点间隔形成的线段）重合。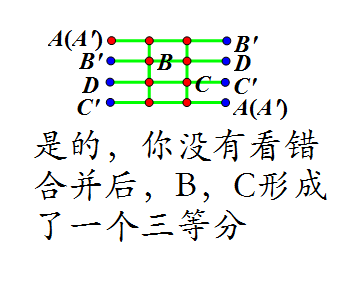

好吧，让我们从代数的角度重新审视一下上面这个东西。设k = n+m，已经保证了k和n是互质的。看下面这段代码。

      

      

for（int i=0;i<n;i++）
    a[i] = i*k%n;
sort（a,a+n）;

在这之后，如果你输入数组a的值，你会得到0,1,2,3....n-1，这样的序列。这是由两个数互质的性质决定的，具体证明可以采用反证法。

然后说了那么多，这个和我们的结论有什么关系呢？

既然所有的节点都到了一段区间，我们就不用管它到底是一个圆还是一条线段，从上面那个图上可以直接看出，B应该往左靠，C应该往右靠。

如果在这种情况下，我们选择转动A点，没转动x，A到最近点的距离增大x，B到最近点的距离增大x,C到最近点的距离减少x，B，C的影响抵消，所以总距离增大，这个增大的趋势一直到A,B,C三个点移动到了四等分该线段的时候，

 ,

然后A的最短距离增大，B,C的最短距离减少，总体距离减少。但是最终再次形成重合的时候，又是一样的。所以先增后尖，最小值在两端。

综合结论1,2该问题圆满解决。也因此获得了上面那个算法，一开始就将所有的关系投影到一个线段上。那个累加ans过程就来自以上分析。

值得一提的是，如果不进行约分的话，在很多情况下，答案也是对的，得益于映射到线段时良好的对称性。但是n和m存在倍数关系就不行了。