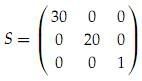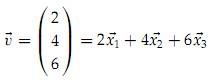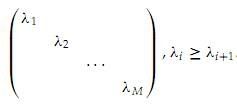SVD奇异值分解
在本文中讨论的矩阵都是实数矩阵。
基础知识
1. 矩阵的秩:矩阵的秩是矩阵中线性无关的行或列的个数
2. 对角矩阵:对角矩阵是除主对角线外所有元素都为零的方阵
3. 单位矩阵:如果对角矩阵中主对角线上的元素都为一,该矩阵称为单位矩阵
4. 特征值:对一个M x M矩阵C和向量X,如果存在λ使得下式成立
则称λ为矩阵C的特征值,X称为矩阵的特征向量。非零特征值的个数小于等于矩阵的秩。
5. 特征值和矩阵的关系:考虑以下矩阵
该矩阵特征值λ1 = 30,λ2 = 20,λ3 = 1。对应的特征向量
假设VT=(2,4,6) 计算S x VT
有上面计算结果可以看出,矩阵与向量相乘的结果与特征值,特征向量有关。观察三个特征值λ1 = 30,λ2 = 20,λ3 = 1,λ3值最小,对计算结果的影响也最小,如果忽略λ3,那么运算结果就相当于从(60,80,6)转变为(60,80,0),这两个向量十分相近。这也表示了数值小的特征值对矩阵-向量相乘的结果贡献小,影响小。这也是后面谈到的低阶近似的数学基础。
矩阵分解
1. 方阵的分解
1) 设S是M x M方阵,则存在以下矩阵分解
![]()
其中U 的列为S的特征向量,![]() 为对角矩阵,其中对角线上的值为S的特征值,按从大到小排列:
为对角矩阵,其中对角线上的值为S的特征值,按从大到小排列:
2) 设S是M x M 方阵,并且是对称矩阵,有M个特征向量。则存在以下分解
![]()
其中Q的列为矩阵S的单位正交特征向量,![]() 仍表示对角矩阵,其中对角线上的值为S的特征值,按从大到小排列。最后,QT=Q-1,因为正交矩阵的逆等于其转置。
仍表示对角矩阵,其中对角线上的值为S的特征值,按从大到小排列。最后,QT=Q-1,因为正交矩阵的逆等于其转置。
2. 奇异值分解
上面讨论了方阵的分解,但是在LSA中,我们是要对Term-Document矩阵进行分解,很显然这个矩阵不是方阵。这时需要奇异值分解对Term-Document进行分解。奇异值分解的推理使用到了上面所讲的方阵的分解。
假设C是M x N矩阵,U是M x M矩阵,其中U的列为CCT的正交特征向量,V为N x N矩阵,其中V的列为CTC的正交特征向量,再假设r为C矩阵的秩,则存在奇异值分解:
![]()
其中CCT和CTC的特征值相同,为![]()
Σ为M X N,其中![]()
![]() ,其余位置数值为0,
,其余位置数值为0,![]() 的值按大小降序排列。以下是Σ的完整数学定义:
的值按大小降序排列。以下是Σ的完整数学定义:
σi称为矩阵C的奇异值。
用C乘以其转置矩阵CT得:
![]()
上式正是在上节中讨论过的对称矩阵的分解。
奇异值分解的图形表示:
从图中可以看到Σ虽然为M x N矩阵,但从第N+1行到M行全为零,因此可以表示成N x N矩阵,又由于右式为矩阵相乘,因此U可以表示为M x N矩阵,VT可以表示为N x N矩阵