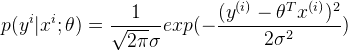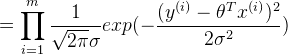机器学习--线性回归

本文转自：



http://blog.csdn.net/linkin1005/article/details/39188599

一、概念

线性回归是利用称为线性回归函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。线性回归函数则是一个或多个称为回归系数的模型参数的线性组合。

二、用途
当结论或者类是数值，并且所有训练样本都为数值时，可以使用线性回归的方法。

线性回归主要用途是预测，线性回归可以利用训练集拟合出一个预测模型。当完成这样一个模型以后，对于一个新增的x值，在没有给定与它相配对的y的情况下，可以用这个拟合过的模型预测出一个y值。

三、模型

输入：m个训练样本，,...,；

输出：n个线性方程的回归系数，。

线性回归方程可以表示为自变量x与因变量h(x)的线性组合：

(1)

     注：这里称为参数（也称权值）。

     通过对训练样本的学习，确定参数使得样本y和预测值h(x)之间最接近。我们用代价函数表示样本y和预测值h(x)之间的距离：

                               (2)

我们的目的是使最小，即求出min。

四、实现

规范式（normal equation）

规范式是通过公式直接计算出使得代价函数取最小值的的值：

令

          

得到.

梯度下降算法（gradient descent）

梯度下降算法是一种搜索算法，其基本思想是赋予一个初始值，然后通过迭代的方法不断更新的值以使达到最小：

                                                                                                    （3）

这里，被称为学习率（learning rate），的大小决定梯度下降的速率。

为求我们先看的各分量：

                                   

                                 

                                                               （4）

那么对于单一的样本,将公式（4）带入公式（3）得：

           

上述更新方法称为LMS更新规则（least mean squares rules），也称Windrow-Hoff学习规则，该方法有如下性质：迭代的速率与误差项（error term）以及的值正相关：如果过小，收敛的速率很慢；反之，若过大，则迭代的速率过快，可能导致不收敛的情况。

Windrow-Hoff学习方法仅仅考虑单个训练样本，样本的选取对于对于迭代次数有一定的影响，若选取的是极端样本，可能导致迭代次数过多或者无法收敛的情况。将Windrow-Hoff学习方法略作修改，便可得到利用多样本的梯度下降学习方法：

批梯度下降算法（batch gradient descent）

Repeat until convergence{

   (for every j)

}

批梯度下降算法使用了所有的样本，因此得名。

随机梯度下降算法（stochatic gradient descent）

for (j=1;j<=n;j++){

for( i=1;i<= m;i++){

          

if (convergence) 

break;

}

}

批梯度下降算法在进行首次迭代前，就需要扫描所有训练样本，如果样本量较大的话，可能会产生较大开销。而随机梯度下降算法可立即迭代，在每次迭代时引入一个样本。随机梯度下降算法由于每次迭代的步长均不同，因此可能会产生不收敛的现象。但通常，随机梯度下降算法比批梯度下降算法收敛速率更快。因此，若数据量较大的情况下，一般更倾向于使用随机梯度下降算法。

五、原理（为何使用最小二乘）

假设和满足如下关系：

                                                                         (5)

其中，是误差项，表示未参与建模的因素产生的误差。

更进一步的假设为独立同分布（independently and identicallydistributed, IID），并服从期望为0，方差为的正态分布。即，那么的密度函数为：

                                                    (6)

由（5）和（6）可得

                                                                                                    (7)

 表示给定 和参数的情况下， 的分布。关于的极大似然方程为：

                                                                                      

                                                                                                                              (8)

我们在样本给定的情况下，通过改变的值，使得样本的联合分布概率最大，即使最大。

的对数似然函数为：

                                                                                   

                                                                                             

                                                                                               

                                                                                                         (9)

（9）的前项为常数，后项非负。因此，当取最小值时，有最大值。而后项中为最小二乘的代价函数。

由此可见，计算的极大似然函数过程中，很自然的会选择最小二乘代价函数。