hihoCoder#1032_最长回文子串

求最长回文子串的算法比较经典的是manacher算法，下面写写自己的理解。

(文中用到的图片来自这里，博主写的很好，由于为了图片和代码一致，我稍微p了一下图片。)

首先，说明一下用到的数组和其他参数的含义：

（1）：

      以字符串中下标为的字符为中心的回文子串半径长度；

例如：字符串，那么，    （以b为中心的回文子串是，半径长度为2。计算半径时包括b本身）

所以，数组的最大值就是最长回文串的半径。

（2）

   为当前已确定的边界能伸展到最靠右的回文串的中心。

  例如：

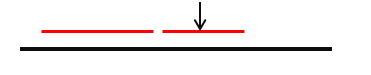
设黑色的线段表示字符串范围，红色的线段表示当前已经确定的回文子串在主串中的范围，虽然左边的红色线段（左边的回文子串）长度比右边长，但是，记录的中心是右边红色线段的中心，因为右边的回文子串伸展更靠右。（下面将会解释为什么要记录这个id值）

manacher算法是从左到右扫描的，所以，在计算时，都是已知的。

假设现在扫描到主串下标为的字符，那么，以为中心的回文子串最可能和之前已经确定的哪个回文子串有交集？没错，就是能伸展最靠右的回文子串，也就是以为中心的回文子串。至于这个交集有什么用，下面将解释。

以i为中心的回文串和以id为中心的回文串如果有交集，会出现三种情况：

（1）

其中，2*id-i为i以id为中心的对称位置。（2*id-i这个就不用多说了吧，计算一下就得到了）

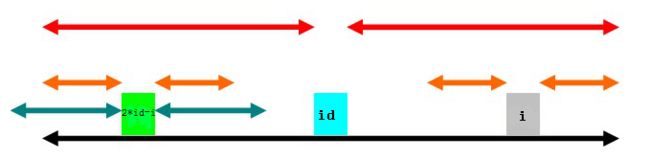
第一种情况是（上图），以2*id-i为中心的回文子串左端超出了以id为中心的回文子串（绿色部分左端超出黑色部分左端）。那么，根据回文串的特点，知道以2*id-i为中心的两边橙色部分是对称的，同样，若以id为中心，这两段橙色部分又对称id右边两段橙色部分，所以，以i为中心的两段橙色部分也是回文串。

这种情况下，       (橙色部分的长度)

那么，以i为中心的橙色部分有没有可能更长？这是不可能的，假设还可以更长，如下：

a和b对称，b和c对称，c和d对称，最终得到a和d对称，那么，以id为中心的回文串长度就不是下面黑色部分的长度了，而应左端加a右端加d，与已经求得的长度矛盾。

所以这种情况下；

（2）

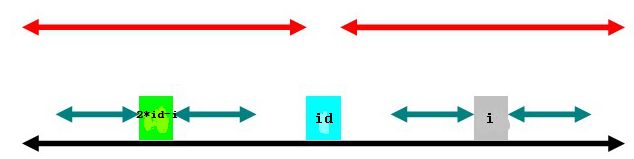
第二种情况是以2*id-i为中心的回文子串在以id为中心的回文子串内，如上图。此时，，那么，以i为中心的绿色部分还可以伸展吗？假设可以，如下：

同样，c和d对称，b和c对称，a和d对称，得到a和b对称，那么以2*id-i为中心的回文子串长度就不是绿色部分的长度了，需要左端加a右端加b，与以求得的长度矛盾。

所以，这种情况下。

（3）

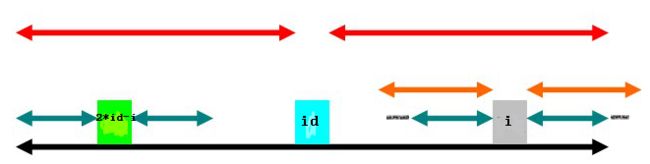
第三种情况是，以2*id-i为中心的回文子串左端与以id为中心的回文子串的左端恰好重合。则有。也就是说在的基础上，还可能增加，即以i为中心的绿色部分还可能伸展。

所以，需要用一个while循环来确定它能增加多少。while循环为：

while (s[i - p[i]] == s[i + p[i]])
	++p[i];

也就是判断绿色两端（下图浅黑色线段）是否相同，如果相同，就可以不断增加。（理解p[i]的意思，就理解这个循环了）

如果没有出现交集(上面三种情况)，那么就以i为中心点找最长回文子串(下面代码中else的情况)。所以，算法主要是利用回文串的交集来减少计算。

如果我们将上面的情况总结起来，代码将非常简洁：

if (p[id] + id - 1 >= i)//没有超出当前边界最右的回文串，也就是上面出现交集三种情况中的一种
     p[i] = Min(p[2 * id - i], p[id] + id - i);
else//如果没有交集，就以它为中心求回文串长度
  p[i] = 1;

while (s[i - p[i]] == s[i + p[i]])
   ++p[i];

最后，需要注意的是，上面的讨论都是以某个字符为中心的回文串，比如像这样的回文串：aabaa(长度为奇数)。但是，如果是这样的回文串：aabbaa(长度为偶数)，就没法处理。

我们可以通过插入特殊符号（如‘#’）的办法，将字符串统一为奇数长度，如aabaa变为#a#a#b#a#a#  ;同理，aabbaa变为#a#a#b#b#a#a# 

注意到，上面的代码：

while (s[i - p[i]] == s[i + p[i]])
     ++p[i];

可能越界(超过头或尾),我们可以通过头尾也加入不相同的特殊符号处理，如aabaa变为$#a#a#b#a#a#@。这种办法为什么可行呢？我们举个例子，还是以aabaa为例，它变成$#a#a#b#a#a#@。当i指向第一个a时（也就是i=2），这时，s[i-1]==s[i+1]；继续比较s[i-2]≠s[i+2]（也就是比较$和a），就不会超过头。所以，就避免了越界的现象。末尾加个@也是同样的道理。

下面是hihoCoder的一道求最长回文子串的题：http://hihocoder.com/problemset/problem/1032

我的ac代码：

#include<iostream>  
#include<string>  

int Min(int a, int b)
{
	if (a < b)
		return a;
	return b;
}

int LPS(std::string &s)
{
	std::string new_s="";
	int s_len = s.length();

	new_s.resize(2 * s_len + 3);

	int new_s_len = new_s.length();
	
	new_s[0] = '$';
	new_s[1] = '#';
	new_s[new_s_len - 1] = '@';

	for (int i = 0,j=2; i < s_len; ++i)
	{
		new_s[j++] = s[i];
		new_s[j++] = '#';
	}
	
	int *p = new int[new_s_len + 1];
	int id = 0;//记录已经查找过的边界最靠右回文串的中心
	int maxLPS = 1;
	p[0] = 1;
	for (int i = 1; i < new_s_len-1; ++i)
	{
		if (p[id] + id - 1 >= i)//有交集的情况
			p[i] = Min(p[2 * id - i], p[id] + id - i);
		else//无交集的情况
			p[i] = 1;

		while (new_s[i - p[i]] == new_s[i + p[i]])//确定能伸展多少，上面if的情况是不会执行这个循环的
			++p[i];

		if (p[id] + id < p[i] + i)//重新确定伸展最右的回文子串中心
			id = i;
		if (p[i]>maxLPS)//保存当前最长回文子串的长度(还要-1)
			maxLPS = p[i];
	}
	delete[] p;
	return maxLPS - 1;
}

int main()
{
	int N;
	std::string s;
	std::cin >> N;
	while (N--)
	{
		std::cin >> s;
		std::cout<<LPS(s)<<std::endl;
	}
	return 0;
}

在插入特殊符号（$ # @）时，刚开始用insert()函数,超时了，应该是不断insert的原因。后来干脆直接用一个新的字符串保存处理后的字符串，就通过了。