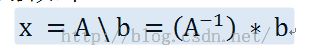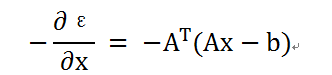MATLAB的人工神经网络应用

一、  人工神经网络简介

    人工神经网络 ( Artifical NeuralNetwork- ANN) 是目前国际上迅速发展的前沿交叉学科 (张立明, 1993), 它是模仿生物神经系统的信息处理方式、 组织结构和系统功能的简化系统。人工神经网络以其自身的自组织、自适应和自学习的特点被广泛应用于各个领域。传统的前馈网络属于静态网络，而今年来迅速发展的递归神经网络，属于动态网络，利用网络的内部状态来反馈描述系统的非线性动力学特性，从而更直接的反应系统的动态特性。

    递归网络是有一个或多个反馈回路的神经网络，把反馈应用于神经网络有多种不中的形式，从而就会产生不同结构的递归网络。在其学习算法中，递归下降法被广泛应用。本文采用一种梯度法神经网络(即Hopfield神经网络或称递归神经网络)求解线性矩阵方程:

 

通过与理论的解对比分析，验证该模型的解线性矩阵方程Ax=b的准确性，并进一步通过误差分析，证实求解的正确性。

二、 梯度法神经网络模型的建立

     自上世纪 80年代中期以来 , 很多研究都把注意力放在矩阵运算的快速算法方面。一般来说,数值算法的最小计算复杂度通常与矩阵维数的立方成正比。所以,当这种串行处理算法应用到维数较大的矩阵实时求解问题时就显得效率不高。有鉴于此,我们也曾提出复杂度与矩阵维数平方成正比的数值算法来解决这类矩阵问题。然而,结果也同样未尽人意,如求解一个60000维矩阵逆运算需要约一个小时的时间。因此 ,许多学者一直在探讨合适的并行计算方案。动力学系统方法是一种非常重要的并行计算方法,能够有效地解决固定矩阵运算问题,随着对神经网络的深入研究,基于递归神经网络的动力学系统和模拟求解方法已经发展成熟。神经动力学方法,因其并行分布计算的特性和简单的硬件/电路可实现性,被认为是在线解决这些固定矩阵运算问题的强有力的替换工具。

 

2.1 理论解

数学矩阵论中求解方法如下：

 

2.2 模型推导

下面依据负梯度设计方法推导该神经网络模型:

1)构造一个基于矩阵范数的标量误差函数 :

2)为了使上述误差减小 , 可使用经典的负梯度方法, 因此我们可以得到如下误差函数负梯度方向作为下降方向:

3)线性的基于负梯度的神经网络模型如下:

其中参数  决定网络的收敛速度(如条件允许, 越大越好);

三、梯度法神经网络模型解线性矩阵方程Ax=b结果的验证

通过数学矩阵论中求出的解与梯度法神经网络模型求出的解x的比较分析，以及误差分析来检验该神经网络在求解线性矩阵方程问题时的准确性和有效性。模型的验证我们通过MATLAB仿真来实现。

 

3.1 MATLAB程序分析

3．1.1构造矩阵

为了仿真 、 对比和验证上文给出 的分析结论 , 我们可以考虑与如下常系数矩阵相关的矩阵方程的神经网络求解：

                                          

且矩阵A、b可以由下面MATLAB代码给出：

构造矩阵A

matirxA.m

function A=matirxA()

A=[1 2  3; 4  2  6;7  4 9];  %任意给出n阶方阵

 

构造矩阵B

Vector.m

function b=vectorb()

b=[1; 1; 3];      %任意给出与矩阵同行的行矩阵

 

3.1.2 AX=b 理论解的求解

main.m

%理论解的求解

A=matrixA(t);

b=vectorb(t);

y=A\b;

t1=0:0.01:10

 

%画出理论解y1 y2 y3的图形

plot(t1, y(1), '.b', t1, y(2), '.r', t1,y(3), '.k')

legend('理论解x1','理论解x2','理论解x3');

xlabel('t');

ylabel('x');

hold on

x1= y(1), x2=y(2),x3=y(3)       %输出理论解

 

3.1.3 梯度法神经网络模型解线性矩阵方程Ax=b

先将描述该神经网络的矩阵微分方程 (MDE)转化为向量微分方程(VDE) ,即标准的给定初始值常微分方程 (ODE) ; 再用MATLAB 指令“ode15s ”, 用来仿真上述转化后的给定初始值常微分方程，最后再将x随时间t变化的过程绘出。

（1）矩阵微分方程转换为向量微分方程

xprim3.m

function xprim=xprim3(t,x)

lamda=100;    %lamda即模型中的参数    决定网络的收敛速度

A=matirxA;

b=vectorb;

xprim=-lamda*A'*(A*x-b); %t时间内 x 沿负梯度方向变化的  的值

 

（2）梯度法神经网络模型求出的 的解以及求解的x的过程图

main.m

clc

clear

close all

t0=[0 2];

x0=[0;0;0];

%ode15s返回值：随时间变化  的值  

% ode15s参数：'xprim3' – 需要求数值解的微分方程的函数

%t0 – 变化的时间     x0 –- x 的初值

% 在时间t自动调整x，求解

[t,x]=ode15s('xprim3',t0,x0); 

plot(t,x);    %画出微分方程求解过程中随时间t变化的曲线

hold off;

 

3.1.4 误差分析

for j=1:length(t)

       err(:,j)=A*x(j,:)'-b; %将神经网络模型求解的x值代入Ax-b中

       nerr(j)=norm(err(:,j));

end

figure

plot(t,nerr)

xlabel('时间t');

 

3.2 MATLAB的运行结果分析

 （1） 理论解的数值

       理论解的数值分别是：

x1 =   0.5000

x2 =   1.0000

x3 =   -0.5000

 

（2）理论解与模型解的图形

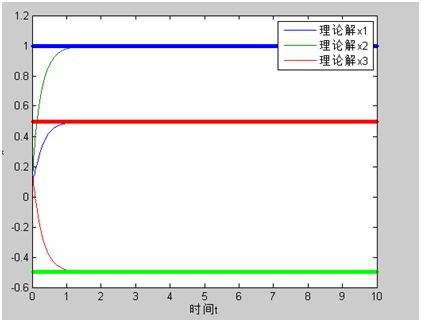
从图1中，理论解x1、理论解x2和理论解x3三条直线是以理论解x1、x2、x3做纵坐标平行于x轴的直线，可以看出当 t>1 时，随着t的增大，梯度法神经网络模型求解线性矩阵方程 的三个解分别越来越接近理论解x1、理论解x2和理论解x3三条直线，说明网络模型求解线性矩阵方程的准确性。

图1

 

（2） 误差分析图形

图2

从误差图图2进一步分析，同样当t>1 时，基于梯度下降法的神经网络模型求解线性方程组结果的误差趋近于0。进一步验证我们的基于梯度下降法的神经网络模型求解线性方程组的模型具有很好的校验。

 

四、结论

仿真结果同理论分析的对应一致,进一步证实基于梯度法的Hopfield神经网络在求解固定系数线性矩阵方程中具有很好的效验。基于梯度法Hopfield神经网络提供了一个有效的实时求解线性矩阵方程的并行计算方法。