【二分图匹配】poj1325Machine Schedule

http://poj.org/problem?id=1325
题目描述：在机器A，B上共有k个要完成的任务。每个任务在A,B上的运行模式不同。A机器有n种模式，B机器有m种模式，机器的初始模式为0。机器每切换一次模式需要重启一次。求最小重启次数。

这是一道经典的二分图匹配问题。
将A机器的模式点放入x集合，B机器的模式点放入y集合。（当然0模式不需要放入，在一开始就可以完成，不需要重启）
对每一个任务，从x集合连一条边至y集合。
问题就转化为为最小点的集合，使得每一条边都被覆盖。（当边有一个端点在集合中，该边就被覆盖）
这里有一个结论：在二分图中，最小点覆盖=最大匹配
证明：
若已知最大匹配如下图所示。只需要选择匹配边的其中一个端点即可。

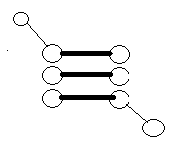
不会存在这种的情况。因为这样形成了一条增广路，不再是最大匹配了。

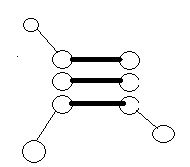
个人认为这里没有说清楚，若有严格证明的大牛，欢迎留下宝贵的建议，以供蒟蒻学习。O(∩_∩)O谢谢

邻接矩阵代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#define MAXN 105
using namespace std;

int n ,m ,k ,a ,cx[MAXN] ,cy[MAXN] ,vis[MAXN] ,b ,c ;
bool map[MAXN][MAXN] ;

bool dfs(int u)
{
    for(int i=1;i<m;++i)
        if(map[u][i]&&!vis[i])
        {
            vis[i]=1;
            if(!cy[i]||dfs(cy[i]))
            {
                cx[u]=i ,cy[i]=u ;
                return 1;
            }
        }
    return 0;
}

void solve()
{
    memset(cx,0,sizeof cx);
    memset(cy,0,sizeof cy);

    int ans=0;
    for(int i=1;i<n;++i)
        if(!cx[i])
        {
            memset(vis,0,sizeof vis);
            ans+=dfs(i);
        }
    printf("%d\n",ans);
}

int main()
{
    while(~scanf("%d",&n)&&n)
    {
        scanf("%d%d",&m,&k);
        memset(map,0,sizeof map);
        for(int i=0;i<k;++i)
        {
            scanf("%d%d%d",&a,&b,&c);
            if(b==0||c==0)continue;
            map[b][c]=1;
        }
        solve();
    }
    return 0;
}

邻接表代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#define MAXN 205
using namespace std;

int n ,m ,k ,a ,b ,c ,cx[MAXN] ,cy[MAXN] ;
bool vis[MAXN] ;

struct node
{
    int v ;
    node *next ;
}edge[MAXN*MAXN] ,*num[MAXN] ,*code=edge ;

void add(int a,int b)
{
    node *p=++code;
    p->v=b ,p->next=num[a];
    num[a]=p;
}

bool dfs(int u)
{
    int v ;
    for(node *p=num[u];p!=NULL;p=p->next)
    {
        v=p->v;
        if(!vis[v])
        {
            vis[v]=1;
            if(!cy[v]||dfs(cy[v]))
            {
                cy[v]=u ,cx[u]=v ;
                return 1;
            }
        }
    }
    return 0;
}

void solve()
{
    memset(cx,0,sizeof cx);
    memset(cy,0,sizeof cy);

    int ans=0;
    for(int i=1;i<n;++i)
        if(!cx[i])
        {
            memset(vis,0,sizeof vis);
            ans+=dfs(i);
        }
    printf("%d\n",ans);
}

int main()
{
    while(~scanf("%d",&n)&&n)
    {
        code=edge;
        memset(num,0,sizeof(num));

        scanf("%d%d",&m,&k);
        for(int i=0;i<k;++i)
        {
            scanf("%d%d%d",&a,&b,&c);
            if(b==0||c==0)continue;
            add(b,c+n);
        }
        solve();
    }
    return 0;
}

不知为何两个时间相同，内存相同= =
应该是邻接表写丑了……