谱聚类
一、复杂网络中的一些基本概念
1、复杂网络的表示
在复杂网络的表示中,复杂网络可以建模成一个图,其中, 表示网络中的节点的集合,
表示网络中的节点的集合,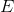 表示的是连接的集合。在复杂网络中,复杂网络可以是无向图、有向图、加权图或者超图。
表示的是连接的集合。在复杂网络中,复杂网络可以是无向图、有向图、加权图或者超图。
2、网络簇结构
网络簇结构
(network cluster structure)
也称为网络社团结构
(network community structure)
,是复杂网络中最普遍和最重要的拓扑属性之一。网络簇是整个网络中的稠密连接分支,具有同簇内部节点之间相互连接密集,不同簇的节点之间相互连接稀疏的特征。
3、复杂网络的分类
复杂网络主要分为:随机网络,小世界网络和无标度网络。
二、谱方法介绍
1、谱方法的思想
在复杂网络的网络簇结构存在着同簇节点之间连接密集,不同簇节点之间连接稀疏的特征,是否可以根据这样的特征对网络中的节点进行聚类,使得同类节点之间的连接密集,不同类别节点之间的连接稀疏?
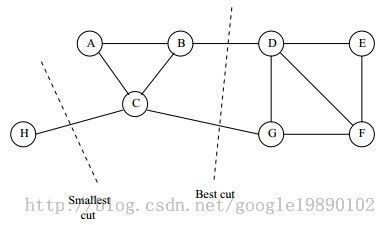
在谱聚类中定义了“截”函数的概念,当一个网络被划分成为两个子网络时,“截”即指子网间的连接密度。谱聚类的目的就是要找到一种合理的分割,使得分割后形成若干子图,连接不同的子图的边的权重尽可能低,即“截”最小,同子图内的边的权重尽可能高。
2、“截”函数的具体表现形式
“截”表示的是子网间的密度,即边比较少。以二分为例,将图聚类成两个类: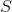 类和
类和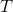 类。假设用
类。假设用 来表示图的划分,我们需要的结果为:
来表示图的划分,我们需要的结果为:
其中表示的是类别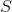 和
和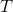 之间的权重。
对于
之间的权重。
对于
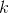 个不同的类别
个不同的类别
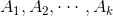 ,优化的目标为:
,优化的目标为:
3、基本“截”函数的弊端
对于上述的“截”函数,最终会导致不好的分割,如二分类问题:
上述的“截”函数通常会将图分割成一个点和其余个点。
4、其他的“截”函数的表现形式
为了能够让每个类都有合理的大小,目标函数中应该使得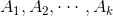 足够大,则提出了
足够大,则提出了 或者:
或者:
其中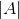 表示
表示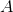 类中包含的顶点的数目
类中包含的顶点的数目
三、Laplacian矩阵
1、Laplacian矩阵的定义
拉普拉斯矩阵
(Laplacian Matrix)
,也称为基尔霍夫矩阵,是图的一种矩阵表示形式。
对于一个有 个顶点的图,其
Laplacian
矩阵定义为:
个顶点的图,其
Laplacian
矩阵定义为:
其中, 为图的度矩阵,
为图的度矩阵,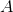 为图的邻接矩阵。
为图的邻接矩阵。
2、度矩阵的定义
度矩阵是一个对角矩阵,主角线上的值由对应的顶点的度组成。
对于一个有 个顶点的图,其邻接矩阵为:
个顶点的图,其邻接矩阵为:
其度矩阵为:
3、Laplacian矩阵的性质
性质3的证明:
4、不同的Laplacian矩阵
除了上述的拉普拉斯矩阵,还有规范化的
Laplacian
矩阵形式:
四、Laplacian矩阵与谱聚类中的优化函数的关系
1、由Laplacian矩阵到“截”函数
对于二个类别的聚类问题,优化的目标函数为:
定义向量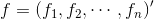 ,且
,且
而![\frac{1}{2}\cdot \left [ \sum_{i\in A,j\in \bar{A}}w_{ij}+\sum_{i\in \bar{A},j\in A}w_{ij} \right ]=\frac{1}{2}\sum_{i=1}^{k}W\left ( A_i,\bar{A}_i \right )=cut\left ( A,\bar{A} \right )](http://latex.codecogs.com/gif.latex?\frac{1}{2}\cdot&space;\left&space;[&space;\sum_{i\in&space;A,j\in&space;\bar{A}}w_{ij}+\sum_{i\in&space;\bar{A},j\in&space;A}w_{ij}&space;\right&space;]=\frac{1}{2}\sum_{i=1}^{k}W\left&space;(&space;A_i,\bar{A}_i&space;\right&space;)=cut\left&space;(&space;A,\bar{A}&space;\right&space;))
而}{\left&space;|&space;A&space;\right&space;|}+\frac{cut\left&space;(&space;A,\bar{A}&space;\right&space;)}{\left&space;|&space;\bar{A}&space;\right&space;|}&space;\right&space;)=\sum_{i=1}^{k}\frac{cut\left&space;(&space;A_i,\bar{A}_i&space;\right&space;)}{\left&space;|&space;A_i&space;\right&space;|}=RatioCut\left&space;(&space;A,\bar{A}&space;\right&space;))
其中, 表示的是顶点的数目,对于确定的图来说是个常数。由上述的推导可知,由推导出了,由此可知:
Laplacian
矩阵与有优化的目标函数之间存在密切的联系。
表示的是顶点的数目,对于确定的图来说是个常数。由上述的推导可知,由推导出了,由此可知:
Laplacian
矩阵与有优化的目标函数之间存在密切的联系。
2、新的目标函数
由上式可得:
由于 是个常数,故要求的最小值,即求的最小值。则新的目标函数为:
是个常数,故要求的最小值,即求的最小值。则新的目标函数为:
其中
3、转化到Laplacian矩阵的求解
假设 是
Laplacian
矩阵
是
Laplacian
矩阵 的特征值,
的特征值,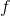 是特征值
是特征值 对应的特征向量,则有:
对应的特征向量,则有:
在上式的两端同时左乘
已知,则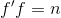 ,上式可以转化为:
,上式可以转化为:
要求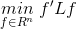 ,即只需求得最小特征值
,即只需求得最小特征值 。由
Laplacian
矩阵的性质可知,
Laplacian
矩阵的最小特征值为
。由
Laplacian
矩阵的性质可知,
Laplacian
矩阵的最小特征值为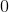 。由
Rayleigh-Ritz
理论,可以取第2小特征值。
。由
Rayleigh-Ritz
理论,可以取第2小特征值。
五、从二类别聚类到多类别聚类
1、二类别聚类
对于求解出来的特征向量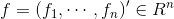 中的每一个分量
中的每一个分量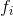 ,根据每个分量的值来判断对应的点所属的类别:
,根据每个分量的值来判断对应的点所属的类别:
2、多类别聚类
对于求出来的前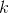 个特征向量,可以利用
K-Means
聚类方法对其进行聚类,若前
个特征向量,可以利用
K-Means
聚类方法对其进行聚类,若前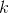 个特征向量为
个特征向量为 ,这样便由特征向量构成如下的特征向量矩阵:
,这样便由特征向量构成如下的特征向量矩阵:
将特征向量矩阵中的每一行最为一个样本,利用K-Means聚类方法对其进行聚类。
六、谱聚类的过程
1、基本的结构
基于以上的分析,谱聚类的基本过程为:
- 对于给定的图,求图的度矩阵
 和邻接矩阵
和邻接矩阵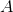 ;
; - 计算图的Laplacian矩阵;
- 对Laplacian矩阵进行特征值分解,取其前
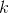 个特征值对应的特征向量,构成
个特征值对应的特征向量,构成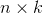 的特征向量矩阵;
的特征向量矩阵; - 利用K-Means聚类算法对上述的
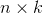 的特征向量矩阵进行聚类,每一行代表一个样本点。
的特征向量矩阵进行聚类,每一行代表一个样本点。
2、利用相似度矩阵的构造方法
上述的方法是通过图的度矩阵 和邻接矩阵
和邻接矩阵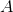 来构造Laplacian矩阵,也可以通过相似度矩阵的方法构造Laplacian矩阵,其方法如下:
来构造Laplacian矩阵,也可以通过相似度矩阵的方法构造Laplacian矩阵,其方法如下:
相似度矩阵是由权值矩阵得到:
其中
再利用相似度矩阵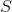 构造
Laplacian
矩阵:
构造
Laplacian
矩阵:
其中 为相似度矩阵
为相似度矩阵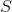 的度矩阵。
的度矩阵。
注意:在第一种方法中,求解的是Laplacian矩阵的前![]() 个最小特征值对应的特征向量,在第二种方法中,求解的是Laplacian矩阵的前
个最小特征值对应的特征向量,在第二种方法中,求解的是Laplacian矩阵的前![]() 个最大特征值对应的特征向量
个最大特征值对应的特征向量
#coding=utf-8
#MSC means Multiple Spectral Clustering
import numpy as np
import scipy as sp
import scipy.linalg as linalg
import networkx as nx
import matplotlib.pyplot as plt
%pylab inline
%matplotlib inline
def getNormLaplacian(W):
"""input matrix W=(w_ij)
"compute D=diag(d1,...dn)
"and L=D-W
"and Lbar=D^(-1/2)LD^(-1/2)
"return Lbar
"""
d=[np.sum(row) for row in W]
D=np.diag(d)
L=D-W
#Dn=D^(-1/2)
Dn=np.power(np.linalg.matrix_power(D,-1),0.5)
Lbar=np.dot(np.dot(Dn,L),Dn)
return Lbar
def getKSmallestEigVec(Lbar,k):
"""input
"matrix Lbar and k
"return
"k smallest eigen values and their corresponding eigen vectors
"""
eigval,eigvec=linalg.eig(Lbar)
dim=len(eigval)
#查找前k小的eigval
dictEigval=dict(zip(eigval,range(0,dim)))
kEig=np.sort(eigval)[0:k]
ix=[dictEigval[k] for k in kEig]
return eigval[ix],eigvec[:,ix]
def checkResult(Lbar,eigvec,eigval,k):
"""
"input
"matrix Lbar and k eig values and k eig vectors
"print norm(Lbar*eigvec[:,i]-lamda[i]*eigvec[:,i])
"""
check=[np.dot(Lbar,eigvec[:,i])-eigval[i]*eigvec[:,i] for i in range(0,k)]
length=[np.linalg.norm(e) for e in check]/np.spacing(1)
print("Lbar*v-lamda*v are %s*%s" % (length,np.spacing(1)))
g=nx.karate_club_graph()
nodeNum=len(g.nodes())
m=nx.to_numpy_matrix(g)
Lbar=getNormLaplacian(m)
k=2
kEigVal,kEigVec=getKSmallestEigVec(Lbar,k)
print("k eig val are %s" % kEigVal)
print("k eig vec are %s" % kEigVec)
checkResult(Lbar,kEigVec,kEigVal,k)
#跳过k means,用最简单的符号判别的方法来求点的归属
clusterA=[i for i in range(0,nodeNum) if kEigVec[i,1]>0]
clusterB=[i for i in range(0,nodeNum) if kEigVec[i,1]<0]
#draw graph
colList=dict.fromkeys(g.nodes())
for node,score in colList.items():
if node in clusterA:
colList[node]=0
else:
colList[node]=0.6
plt.figure(figsize=(8,8))
pos=nx.spring_layout(g)
nx.draw_networkx_edges(g,pos,alpha=0.4)
nx.draw_networkx_nodes(g,pos,nodelist=list(colList.keys()),
node_color=list(colList.values()),
cmap=plt.cm.Reds_r)
nx.draw_networkx_labels(g,pos,font_size=10,font_family='sans-serif')
plt.axis('off')
plt.title("karate_club spectral clustering")
plt.savefig("spectral_clustering_result.png")
plt.show()
参考自:
http://blog.csdn.net/google19890102/article/details/45697695#
http://blog.csdn.net/leepwang/article/details/7631017