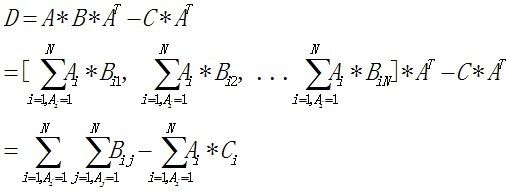HDU 4037 Matrix 最小割模型转换

题意：给定一个n*n（n<=1000）的B矩阵和1*n的C矩阵，现在想找到合适的1*n的A矩阵，使得D = （A * B - C） * AT的值最大。

题解：化简得到

第一项是定值，题目转换为要最小化后面的三项之和，抽象到最小割模型求解。
建图，令源为s，汇为t，中间有n个点。点i到j有一条容量为B[i][j]的边，同时s到点i有一条容量为C[i]的边，点i到t有一条容量为sum{j}B[i][j]的边。
这样，图的任意一个割就与一个A一一对应，最小割即为最小的后面三项之和。简单解释下任意一个割与一个A一一对应：

首先明确后三项即为在B矩阵中所有sigma Bij（A[i] == 0 || A[j] == 0），所以对于任意一点i，s - i （A[i] == 1）或者i - t（A[i] == 0）必选其中之一，如果A[i] == 1则对于所有j（A[j]== 0）来说，存在s – j – i – t的增广路，所以j– i就一定要包含在该割内，对应即为B[j][i]，所以任意一个割与一个A一一对应。

Sure原创，转载请注明出处。

#include <iostream>
#include <cstdio>
#include <memory.h>
using namespace std;
const int inf = 1 << 29;
const int maxn = 1010;
const int maxe = 2100000;
struct node
{
    int v,w;
    int next;
}edge[maxe];
int head[maxn],cur[maxn],dis[maxn],gap[maxn],pre[maxn];
int B[maxn][maxn],C[maxn],D[maxn];
int n,s,t,idx,sum;

void init()
{
    memset(head,-1,sizeof(head));
    memset(D,0,sizeof(D));
    scanf("%d",&n);
    s = idx = sum = 0;
    t = n + 1;
    return;
}

void addedge(int u,int v,int w)
{
    edge[idx].v = v;
    edge[idx].w = w;
    edge[idx].next = head[u];
    head[u] = idx++;

    edge[idx].v = u;
    edge[idx].w = 0;
    edge[idx].next = head[v];
    head[v] = idx++;
    return;
}

void read()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            scanf("%d",&B[i][j]);
            D[j] += B[i][j];
            if(i != j) addedge(i,j,B[i][j]);
        }
    }
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&C[i]);
        addedge(s,i,C[i]);
        addedge(i,t,D[i]);
        sum += D[i];
    }
    return;
}

int isap(int N)
{
    memset(gap,0,sizeof(gap));
    memset(dis,0,sizeof(dis));
    for(int i=0;i<N;i++)
    {
        cur[i] = head[i];
    }
    int i,top = s;
    int maxflow = 0,flow = inf;
    gap[s] = N;
    while(dis[s] < N)
    {
        for(i=cur[top];i != -1;i=edge[i].next)
        {
            if(edge[i].w > 0 && dis[top] == dis[edge[i].v] + 1)
            {
                break;
            }
        }
        if(i != -1)
        {
            cur[top] = i;
            if(edge[i].w < flow)
            {
                flow = edge[i].w;
            }
            top = edge[i].v;
            pre[top] = i;
            if(top == t)
            {
                maxflow += flow;
                while(top != s)
                {
                    edge[pre[top]].w -= flow;
                    edge[pre[top]^1].w += flow;
                    top = edge[pre[top]^1].v;
                }
                flow = inf;
            }
        }
        else
        {
            if(--gap[dis[top]] == 0)
            {
                break;
            }
            cur[top] = head[top];
            dis[top] = N;
            for(int j=head[top];j != -1;j=edge[j].next)
            {
                if(edge[j].w > 0 && dis[top] > dis[edge[j].v] + 1)
                {
                    cur[top] = j;
                    dis[top] = dis[edge[j].v] + 1;
                }
            }
            gap[dis[top]]++;
            if(top != s)
            {
                top = edge[pre[top]^1].v;
            }
        }
    }
    return maxflow;
}

int main()
{
    int cas;
    scanf("%d",&cas);
    while(cas--)
    {
        init();
        read();
        printf("%d\n",sum - isap(t+1));
    }
    return 0;
}