基数排序
分配排序的基本思想:排序过程无须比较关键字,而是通过“分配”和“收集”过程来实现排序。它们的时间复杂度可达到线性阶:O(n)。
一、两种多关键码排序方法
最高位优先法(MSD法)。先按k1排序,将序列分成若干子序列,每个子序列中的记录具有相同的k1值;再按k2排序,将每个子序列分成更小的子序列;然后,对后面的关键码继续同样的排序分成更小的子序列,直到按kd排序分组分成最小的子序列后,最后将各个子序列连接起来,便可得到一个有序的序列。前面介绍的扑克牌先按花色再按面值进行排序的方法就是MSD法
最次位优先法(LSD法)。先按kd排序,将序列分成若干子序列,每个子序列中的记录具有相同的kd值;再按kd-1排序,将每个子序列分成更小的子序列;然后,对后面的关键码继续同样的排序分成更小的子序列,直到按k1排序分组分成最小的子序列后,最后将各个子序列连接起来,便可得到一个有序的序列。前面介绍的扑克牌先按面值再按花色进行排序的方法就是LSD法。
二、基于LSD方法的链式基数排序的基本思想
“多关键字排序”的思想实现“单关键字排序”。对数字型或字符型的单关键字,可以看作由多个数位或多个字符构成的多关键字,此时可以采用“分配-收集”的方法进行排序,这一过程称作基数排序法,其中每个数字或字符可能的取值个数称为基数。比如,扑克牌的花色基数为4,面值基数为13。在整理扑克牌时,既可以先按花色整理,也可以先按面值整理。按花色整理时,先按红、黑、方、花的顺序分成4摞(分配),再按此顺序再叠放在一起(收集),然后按面值的顺序分成13摞(分配),再按此顺序叠放在一起(收集),如此进行二次分配和收集即可将扑克牌排列有序。
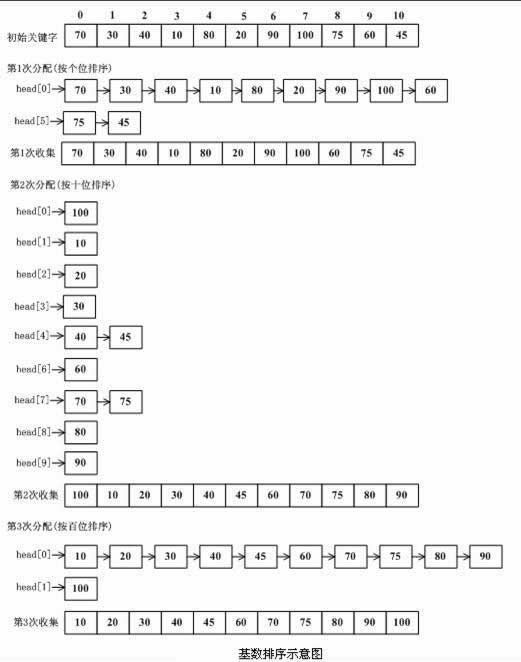
三、基数排序的实现
public
class
RadixNode
<
T
>
{
private T data; // 数据域
private RadixNode < T > next; // 引用域
public RadixNode(T val, RadixNode < T > p)
{
data = val;
next = p;
}
public RadixNode(RadixNode < T > p)
{
next = p;
}
public RadixNode(T val)
{
data = val;
next = null ;
}
public RadixNode()
{
data = default (T);
next = null ;
}
// 数据域属性
public T Data
{
get
{
return data;
}
set
{
data = value;
}
}
// 引用域属性
public RadixNode < T > Next
{
get
{
return next;
}
set
{
next = value;
}
}
}
{
private T data; // 数据域
private RadixNode < T > next; // 引用域
public RadixNode(T val, RadixNode < T > p)
{
data = val;
next = p;
}
public RadixNode(RadixNode < T > p)
{
next = p;
}
public RadixNode(T val)
{
data = val;
next = null ;
}
public RadixNode()
{
data = default (T);
next = null ;
}
// 数据域属性
public T Data
{
get
{
return data;
}
set
{
data = value;
}
}
// 引用域属性
public RadixNode < T > Next
{
get
{
return next;
}
set
{
next = value;
}
}
}
//
对顺序列表sqList进行关键字为m位整型值的基数排序
public void radixSort(SeqList < int > sqList, int n, int m)
{
int i, j, k, l, power;
RadixNode < int > p, q;
RadixNode < int > [] head = new RadixNode < int > [ 10 ];
power = 1 ;
for (i = 0 ; i < m; i ++ )
{
if (i == 0 )
power = 1 ;
else
power = power * 10 ;
for (j = 0 ; j < 10 ; j ++ )
{
head[j] = new RadixNode < int > (); ;
}
for (l = 0 ; l < n; l ++ )
{
k = sqList.Data[l] / power - (sqList.Data[l] / (power * 10 )) * 10 ;
q = new RadixNode < int > ();
q.Data = sqList.Data[l];
q.Next = null ;
p = head[k].Next;
if (p == null )
head[k].Next = q;
else
{
while (p.Next != null ) p = p.Next;
p.Next = q;
}
}
/* 按照链的顺序收回各记录 */
l = 0 ;
for (j = 0 ; j < 10 ; j ++ )
{
p = head[j].Next;
while (p != null )
{
sqList.Data[l] = p.Data;
l ++ ;
p = p.Next;
}
}
}
}
public void radixSort(SeqList < int > sqList, int n, int m)
{
int i, j, k, l, power;
RadixNode < int > p, q;
RadixNode < int > [] head = new RadixNode < int > [ 10 ];
power = 1 ;
for (i = 0 ; i < m; i ++ )
{
if (i == 0 )
power = 1 ;
else
power = power * 10 ;
for (j = 0 ; j < 10 ; j ++ )
{
head[j] = new RadixNode < int > (); ;
}
for (l = 0 ; l < n; l ++ )
{
k = sqList.Data[l] / power - (sqList.Data[l] / (power * 10 )) * 10 ;
q = new RadixNode < int > ();
q.Data = sqList.Data[l];
q.Next = null ;
p = head[k].Next;
if (p == null )
head[k].Next = q;
else
{
while (p.Next != null ) p = p.Next;
p.Next = q;
}
}
/* 按照链的顺序收回各记录 */
l = 0 ;
for (j = 0 ; j < 10 ; j ++ )
{
p = head[j].Next;
while (p != null )
{
sqList.Data[l] = p.Data;
l ++ ;
p = p.Next;
}
}
}
}
四、时间复杂度分析
时间效率:设待排序列为n个记录,d个关键码,关键码的取值范围为radix,则进行链式基数排序的时间复杂度为O(d(n+radix)),其中,一趟分配时间复杂度为O(n),一趟收集时间复杂度为O(radix),共进行d趟分配和收集。