Experimental Educational Round: VolBIT Formulas Blitz题解

传送门

A. Again Twenty Five!

输出5^n的最后两位数，随便写几个就能找到规律了

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
    ll n; 
    cin >> n;
    cout << 25;
    return 0;
}

B. Moore’s Law

就是求n*(1.000000011^m)，用一个快速幂就行了

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll n, m;
double modexp_recursion(double a,int b)     //快速幂，求a^b 
{    
    double t = 1;
    if (b == 0)
        return 1;
    if (b == 1)
         return a;
    t = modexp_recursion(a, b>>1);
    t = t*t;
    if (b&0x1)
        t = t*a;
    return t;
 } 
int main()
{
    double time = 1.000000011, t;
    cin >> n >> m;
    t = modexp_recursion(time, m);
    cout.setf(ios::fixed);
    cout << setprecision(30) << n*t;
    return 0;
}

C - Lucky Numbers

Lucky number是只含有7和8的数，求不超过n位的数中，Lucky number的个数

对于m位数，每一位只能是7或8，共有2^m种，
所以结果就是2^1+2^2+……+2^n=2^(n+1)-2

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
    ll n;
    cin >> n;
    cout << (ll)((ll)1<<(n+1))-2;
    return 0;
}

D. Hexagons!

如上图
计算前n圈一个有多少个六边形
找规律

n=1的时候

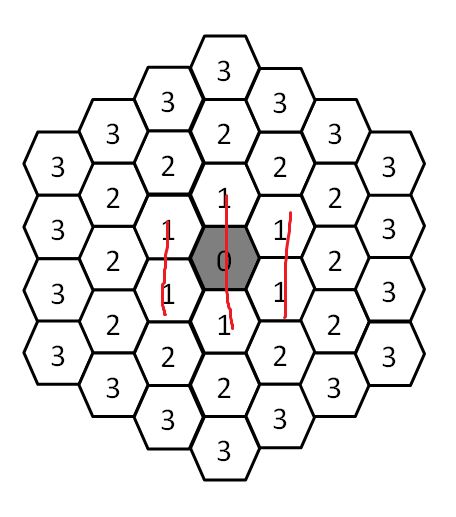
结果是2+3+2
n=2的时候

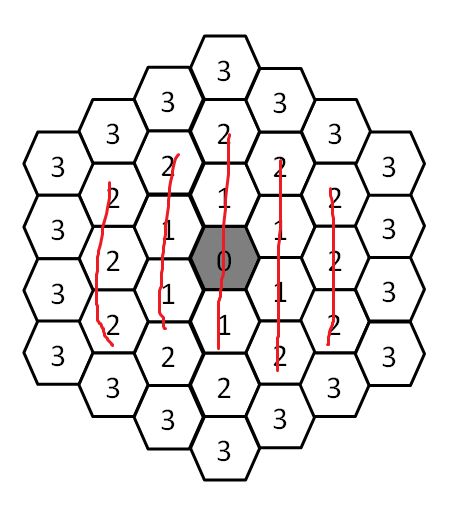
结果是3+4+5+4+3
n=3的时候

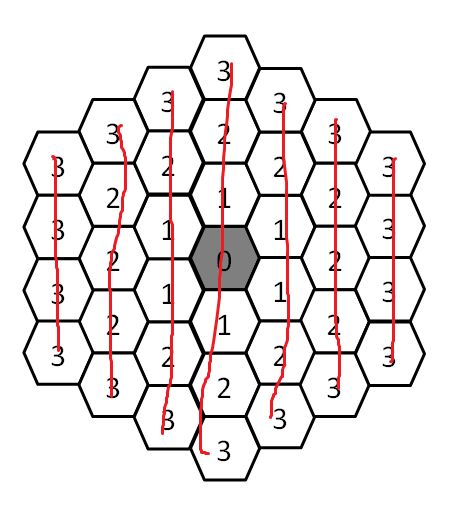
结果是4+5+6+7+6+5+4
…….
所以结果就是n*(3*n+1)+2*n+1

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
    ll n;
    cin >> n;
    cout << n*(3*n+1)+2*n+1;
    return 0;
}

E. A rectangle

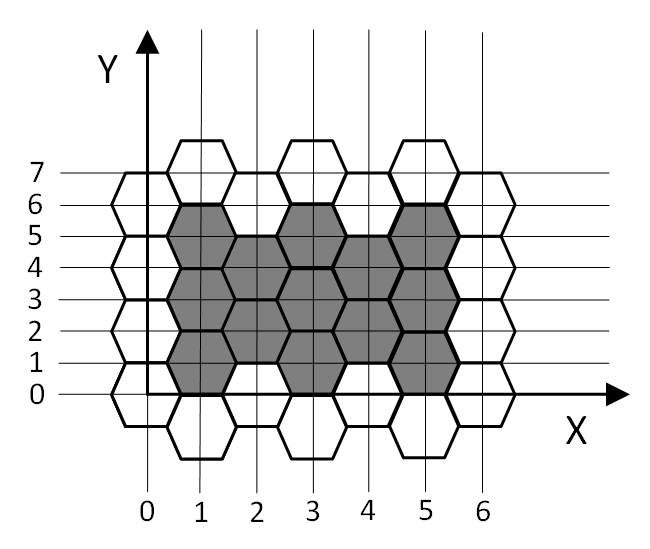
如上图
计算(x₁, y₁), (x₂, y₂)中间所包含的六边形的中心点的个数

同样是找规律
题目保证x₂-x₁是偶数，即x₂和x₁之间有奇数个点，
如果y₂和y₁之间也有奇数个点，答案就是包含总点数的一半再加一
否则就是总点数的一半

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
    ll x1, x2, y1, y2;
    cin >> x1 >> y1 >> x2 >> y2;
    if ((y2-y1+1)%2)
        cout << (x2-x1+1)*(y2-y1+1)/2+1;
    else
        cout << (x2-x1+1)*(y2-y1+1)/2;
    return 0;
}

F. Selection of Personnel

就是计算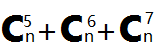 的值
不过计算组合数的时候，如果先乘再除，会溢出，所以要边乘边除

#include <bits/stdc++.h>
#define N 1010
#define ll long long
using namespace std;
ll c(ll n, ll m)
{
    ll ret = 1;
    bool flag[10];
    memset(flag, 0, sizeof(flag));
    for (ll i = 0; i < n; i++)
    {
        ret *= (m-i);
        for (ll i = 1; i <= n; i++)
            if (!flag[i] && ret%i==0)
            {
                ret /= i;
                flag[i] = true;
            }
    }
    return ret;
}
int main()
{
    ll n, ans;
    cin >> n;
    ans += c(5, n)+c(6, n)+c(7, n);
    cout << ans;
    return 0;
}

G. Challenge Pennants

将5个A旗子和3个B旗子插在n个桌子上，有多少种插法
组合数公式，直接计算

#include <bits/stdc++.h>
#define ll long long
using namespace std;
ll c(ll n, ll m)
{
    bool flag[10];
    ll ret = 1;
    memset(flag, 0, sizeof(flag));
    for (int i = 0; i < n; i++)
    {
        ret *= m-i;
        for (int j = 1; j <= n; j++)
        {
            if (!flag[j] && ret%j==0)
            {
                ret /= j;
                flag[j] = true;
            }
        }
    }
    return ret;
}
int main()
{
    ll n, ans;
    cin >> n;
    ans = c(5, n+4)*c(3, n+2);
    cout << ans;
    return 0;
}

H - Benches

先选出5行，再选出5列，再乘5!就是结果了

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
    ll n, ans;
    cin >> n;
    ans = n*(n-1)*(n-2)*(n-3)*(n-4)/120;
    ans *= ans;
    ans *= 120;
    cout << ans;
    return 0;
}

J. Divisibility

计算1到n中，有多少数能被2,3,4,5,6,7,8,9,10整除
最小的能被2,3,4,5,6,7,8,9,10整除的数是8*5*7*9
答案就是n/(8*5*7*9)

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
    ll n, t;
    t = 1*8*5*7*9;
    cin >> n;
    cout << n/t;
    return 0;
}

K. Indivisibility

计算1到n中，有多少不能被2到10中的任意一个数整除
不能被2到10中的任意一个数整除就是不能被2, 3, 5, 7整除
减去能被2,3,5,7整除的数就行了，注意有多减的，需要再加上

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int main()
{
    ll n, ans = 1;
    cin >> n;   //2, 3, 5, 7
    cout << n-n/2-n/3-n/5-n/7+n/6+n/10+n/14+n/15+n/21+n/35-n/30-n/42-n/70-n/105+n/210;
    return 0;
}

L - Cracking the Code

给一个五位数，将它转换成另一个五位数，然后计算它的5次方的最后五位数

#include <bits/stdc++.h>
#define N 55
#define ll long long
#define base 10000
using namespace std;
void mul(int a[], int len, int b) //大数相乘
{
    int carry, i;
    for (i = len-1, carry = 0; i >= 0; i--)
    {
        carry += b*a[i];
        a[i] = carry%base;
        carry /= base;
    }
}
int main()
{
    ll n, m, t;
    int a[N];
    cin >> n;
    t = n;
    m = (t%10)*100;
    t /= 10;
    m += (t%10)*10;
    t /= 10;
    m += (t%10)*1000;
    t /= 10;
    m += t%10;
    t/= 10;
    m += t*10000;
    memset(a, 0, sizeof(a));
    a[N-1] = m%10000;
    a[N-2] = m/10000;
    for (int i = 1; i < 5; i++)
        mul(a, N, m);
    cout << a[N-2]%10;
    cout << setw(4) << setfill('0') << a[N-1];
    return 0;
}

M. Turn

相机旋转x度，则照出来的照片就旋转-x度，求旋转的最小次数，使得照片与垂直方向的夹角最小

#include <bits/stdc++.h>
#define N 1010
#define ll long long
using namespace std;
int main()
{
    ll x;
    cin >> x;
    x = (x%360+360)%360;
    if (x >= 315 || x <= 45)    cout << 0;
    else if (x > 45 && x <= 135)    cout << 1;
    else if (x > 135 && x <= 225)   cout << 2;
    else if (x > 225 && x < 315)    cout << 3;
    return 0;
}

N - Forecast

解二元一次方程，题目保证一定有解

#include <bits/stdc++.h>
#define N 1010
#define ll long long
using namespace std;
int main()
{
    ll  a, b, c;
    double x1, x2, d;
    cin >> a >> b >> c;
    d = b*b-4*a*c+0.0;
    d = sqrt(d);
    x1 = (-b+d)/(2.0*a);
    x2 = (-b-d)/(2.0*a);
    if (x2 > x1)    swap(x1, x2);
    cout.setf(ios::fixed);
    cout << setprecision(30) << x1 << endl;
    cout << setprecision(30) << x2 << endl;
    return 0;
}

R. Game

两个人在n*n的网格上涂颜色，可以在不与已经涂过颜色的格子有公共边，问是先手能赢还是后手能赢

如果n是偶数，后手只要跟着先手走，放在与先手中心对称的位置，这样后手会赢
如果n是奇数，先手先在中心位置放一个，然后还是跟着后手走，放在与后手中心对称的地方，这样先手会赢

#include <bits/stdc++.h>
using namespace std;
int main()
{
    long long n;
    cin >> n;
    if (n&1)    cout << 1;
    else cout <<2;
    return 0;
}