POJ 1363 5.2.1 Rails(出栈入栈经典)
http://poj.org/problem?id=1363
Description
There is a famous railway station in PopPush City. Country there is incredibly hilly. The station was built in last century. Unfortunately, funds were extremely limited that time. It was possible to establish only a surface track. Moreover, it turned out that the station could be only a dead-end one (see picture) and due to lack of available space it could have only one track.
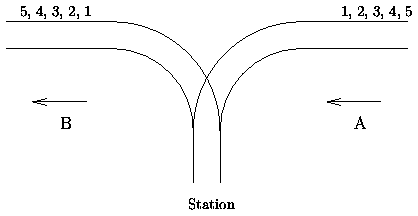
The local tradition is that every train arriving from the direction A continues in the direction B with coaches reorganized in some way. Assume that the train arriving from the direction A has N <= 1000 coaches numbered in increasing order 1, 2, ..., N. The chief for train reorganizations must know whether it is possible to marshal coaches continuing in the direction B so that their order will be a1, a2, ..., aN. Help him and write a program that decides whether it is possible to get the required order of coaches. You can assume that single coaches can be disconnected from the train before they enter the station and that they can move themselves until they are on the track in the direction B. You can also suppose that at any time there can be located as many coaches as necessary in the station. But once a coach has entered the station it cannot return to the track in the direction A and also once it has left the station in the direction B it cannot return back to the station.

The local tradition is that every train arriving from the direction A continues in the direction B with coaches reorganized in some way. Assume that the train arriving from the direction A has N <= 1000 coaches numbered in increasing order 1, 2, ..., N. The chief for train reorganizations must know whether it is possible to marshal coaches continuing in the direction B so that their order will be a1, a2, ..., aN. Help him and write a program that decides whether it is possible to get the required order of coaches. You can assume that single coaches can be disconnected from the train before they enter the station and that they can move themselves until they are on the track in the direction B. You can also suppose that at any time there can be located as many coaches as necessary in the station. But once a coach has entered the station it cannot return to the track in the direction A and also once it has left the station in the direction B it cannot return back to the station.
Input
The input consists of blocks of lines. Each block except the last describes one train and possibly more requirements for its reorganization. In the first line of the block there is the integer N described above. In each of the next lines of the block there is a permutation of 1, 2, ..., N. The last line of the block contains just 0.
The last block consists of just one line containing 0.
The last block consists of just one line containing 0.
Output
The output contains the lines corresponding to the lines with permutations in the input. A line of the output contains Yes if it is possible to marshal the coaches in the order required on the corresponding line of the input. Otherwise it contains No. In addition, there is one empty line after the lines corresponding to one block of the input. There is no line in the output corresponding to the last ``null'' block of the input.
Sample Input
5 1 2 3 4 5 5 4 1 2 3 0 6 6 5 4 3 2 1 0 0
Sample Output
Yes No Yes
Source
具体思路数据结构编程实验P118
(正确)
//注意此算法不能在出现违法的时候提前终止,因为这是一个一个的输入的,提前终止的话后面的就会成为下一组数据了
#include<iostream>
#include<cstring>
using namespace std;
const int maxn=1000+10;
int main()
{
int n,p[maxn]; //记录出入栈的情况 在这里下标其实代表的就是当前的数
cin>>n;
while(n)
{
int x,max=0;
cin>>x; //开始输入新一行中的第一个数
while(x)
{
memset(p,0,sizeof(p)); //开始的时候初始化为全部未入栈
bool valid=true; //valid用来记录当前的出栈入栈(置换)是否合法
for(int i=1;i<=n;i++) //此循环进行一个循环就测验一行数中某一个数的出入合法性
{
bool ok=true; ///////ok使用来记录一行中单个的数进入栈合法性
for(int j=x+1;j<=max;j++) /////检查大于该数到最大值之间的数中是否还有在栈里面的,如果有,直接标记为违法的
if(p[j]==1)
{
ok=false;
break;
}
if(!ok)
valid=false;
else
{
max=(max>x?max:x); ///////查找最大值,用以下一个数检查时的范围
p[x]=2; //将当前数标记为出栈
for(int k=x-1;k>0 && !p[k];k--)//对小于当前数的数进行初始化,令小于当前数都进栈
//但是注意条件如果之前的一个中有已经赋值的就不再向下赋值
p[k]=1;
}
if(i<n)
cin>>x; // 输入本行中下一个数进行检测
}
cout<<(valid ? "Yes" : "No")<<endl;
cin>>x;
}
cout<<endl; //每组数据间的回车符
cin>>n;
}
return 0;
}
未使用栈的解法,只是简单的数组处理,但是在POJ上提交不正确,而在ZOJ上ac了,估计是POJ的测试数据太恶心了,所以谁算法应该是正确的
具体思路(其实比使用栈的思路好像还简单)
将每次输入的先放到a[i]数组中,从该数组中依次检查后比该数(第一个时将其默认为最大值)小但是是必须小1的,如果找到,将这个数的统一下标的b[i]数组设置为1,说明该数已经通过检测,下一次不再进行检测了,然后在继续将找到的作为最大值,继续用该方式进行查找,如果存在比当前最大值小但是不是小1的就证明是错误的,输出测试结果,在进行下一组的测试。
注意在每一组测试时,应该对b进行初始化为0,这样默认为没通过检测。
原本以为这个算法是正确的,但是经过好多人的交流过后,发现这个算法确实是存在bug的,比如3 5 2 4 1这组数据,就是一个错误的数据例子,只是简单的这样遍历是不对的,这也充分说明在ZOJ和UVA的测试数据不是很全的
(存在bug的代码)
#include<iostream>
#include<cstring>
#include <algorithm>
using namespace std;
const int maxn=1000+10;
int main()
{
int a[maxn];
int b[maxn];
int n;
while(cin>>n && n!=0)
{
while(1)
{
memset(b,0,sizeof(b));
int i,j;
int x;
cin>>a[1];
if(a[1]==0)
break;
for(i=2;i<=n;i++)
cin>>a[i];
int max;
int t=true;
for(i=1;i<=n;i++)
{
if(b[i]!=1)
{
b[i]=1;
max=a[i];
for(j=i+1;j<=n;j++)
{
if(a[j]<max&&b[j]!=1)
{
if(a[j]!=max-1)
{
t=false;
break;
}
else
{
max--;
b[j]=1;
}
}
}
}
if(t==false)
break;
}
cout<<(t?"Yes":"No")<<endl;
}
cout<<endl;
}
return 0;
}