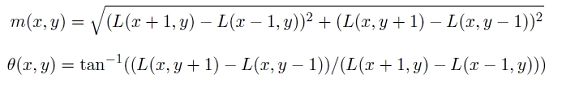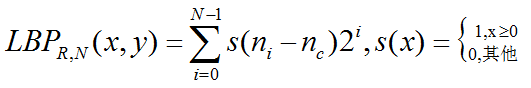使用局部二进制模型改进SIFT描述方法(Description of interest regions with local binary patterns)
Description of interest regions with local binary patterns
该文章发表在Pattern recognition, 2009上,主要针对sift特征表达方法计算量大的问题(因为sift表达方法要计算梯度的方向和大小),提出用CS-LBP来表示sift特征,在降低计算量的同时保证了特征表达的准确性。
如图所示,为了得到梯度的方向和幅值,sift表达方法需要进行开根和反三角函数操作,这是一个费时费力的计算:
作者认为利用更为简单的LBP(局部二进制模型)也能实现类似的表达,具体方法如下:
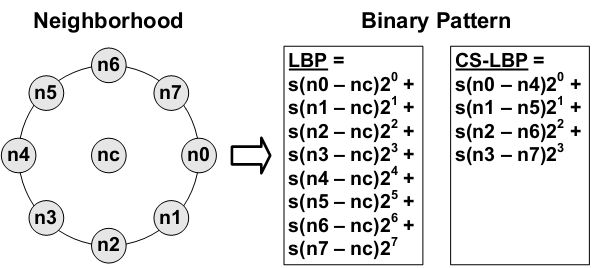
LBP利用相邻像素与中心像素的差值构成的二进制串来表示该位置的纹理,作者提出的中心对称二进制模型(CS-LBP)则是用关于中心像素点对称的两个像素点差值所构成二进制串来表示该位置纹理,与梯度计算相比,LBP特别是CS-LBP只需要做几次加减法就能表示该区域的纹理特性,极大地降低了计算量,因此在计算速度上有了明显提高。
在表达上,传统LBP认为当两个点灰度值之差大于0时便不同,这种方法抗噪声能力太弱。
这里CS-LBP做了一点改进:
作者增加了一个阈值T作为判断条件,这样可以增加图像的抗噪声能力。
将每块需要表示的区域划分成块M*M的块,每块利用CS-LBP(N个邻居)进行表示,这样就会产生M*M*2^(N/2)维特征向量,这就是最终的表示方式。
上图为最终特征向量生成的示意图,首先将表示区域划分为4*4共16个格子,在每个格子内计算每一个像素的CS-LBP值,然后按照方向进行累加,最后每个格子都会得到一个维度为16的特征,经过均一化后整个表示区域就被表示成为16*16即256维度的特征。
上图为CS-LBP与SIFT梯度表示方法的速度比,最上方的是256维的CS-LBP,中间的是128维的CS-LBP,下方的是128维的SIFT梯度表示,可以看出CS-LBP运算速度远远高于SIFT梯度表示方法。
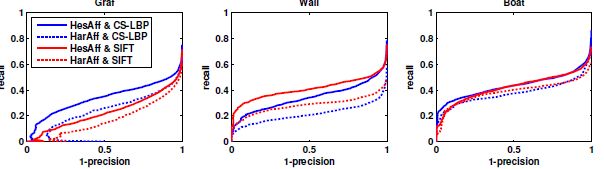
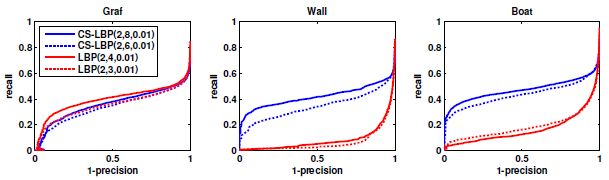
最后,给出ROC曲线图,从结果来看,CS-LBP的精度不比梯度表示法差,在一些项目中甚至明显胜过梯度表示法。