HDU 5015 233 Matrix（矩阵快速幂）

Description
一个(n+1)*(m+1)的矩阵a，a[0][0]=0,a[0][1]=233,a[0][2]=2333,…，a[i][j]=a[i-1][j]+a[i]j-1，现输入a[1][0],…,a[m][0]，求a[n][m](mod 10000007)
Input
多组用例，每组用例第一行为两个整数n和m，之后为m个数表示a[1][0],…,a[m][0]，以文件尾结束输入
Output
对于每组用例，输出a[n][m](mod 10000007)
Sample Input
1 1
1
2 2
0 0
3 7
23 47 16
Sample Output
234
2799
72937
Solution
以n=3为例，构造辅助一个(n+2)*(m+1)的矩阵A

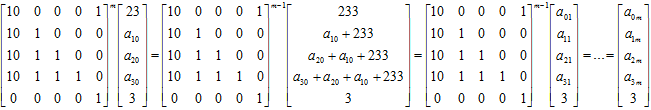
所以对于任一个n，类似上例构造矩阵A，用矩阵快速幂加速求出A^m，然后再乘上矩阵B=[23,a[1][0],…,a[m][0],3]，结果矩阵的第n+1个元素即为a[n][m]
Code

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
#define maxn 15
typedef long long ll;
#define mod 10000007
struct Mat
{
    ll mat[maxn][maxn];//矩阵 
    int row,col;//矩阵行列数 
};
Mat mod_mul(Mat a,Mat b,int p)//矩阵乘法 
{
    Mat ans;
    ans.row=a.row;
    ans.col=b.col;
    memset(ans.mat,0,sizeof(ans.mat));
    for(int i=0;i<ans.row;i++)      
        for(int k=0;k<a.col;k++)
            if(a.mat[i][k])
                for(int j=0;j<ans.col;j++)
                {
                    ans.mat[i][j]+=a.mat[i][k]*b.mat[k][j];
                    ans.mat[i][j]%=p;
                }
    return ans;
}
Mat mod_pow(Mat a,int k,int p)//矩阵快速幂 
{
    Mat ans;
    ans.row=a.row;
    ans.col=a.col;
    for(int i=0;i<a.row;i++)
        for(int j=0;j<a.col;j++)
            ans.mat[i][j]=(i==j);
    while(k)
    {
        if(k&1)ans=mod_mul(ans,a,p);
        a=mod_mul(a,a,p);
        k>>=1;
    }
    return ans;
}
int n,m;
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        if(!n)
        {
            printf("0\n");
            continue;
        }
        Mat A,B;
        B.row=n+2,B.col=1;
        B.mat[0][0]=23ll,B.mat[n+1][0]=3ll;
        for(int i=1;i<=n;i++)scanf("%lld",&B.mat[i][0]);
        A.row=A.col=n+2;
        memset(A.mat,0,sizeof(A.mat));
        for(int i=0;i<n+1;i++)A.mat[i][0]=10ll;
        for(int i=0;i<n+2;i++)A.mat[i][n+1]=1ll;
        for(int i=1;i<=n;i++)
            for(int j=1;j<=i;j++)
                A.mat[i][j]=1ll;
        A=mod_pow(A,m,mod);
        B=mod_mul(A,B,mod);
        printf("%lld\n",B.mat[n][0]);
    }
    return 0;
}