HDU 4568 (SPFA 状压DP)
Hunter
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1738 Accepted Submission(s): 519
Problem Description
One day, a hunter named James went to a mysterious area to find the treasures. James wanted to research the area and brought all treasures that he could.
The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can't cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can't remember whether the point are researched or not).
Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.
The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can't cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can't remember whether the point are researched or not).
Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.

Input
The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case begins with a line containing 2 integers N M , (1<=N,M<=200), that represents the rectangle. Each of the following N lines contains M numbers(0~9),represent the cost of each point. Next is K(1<=K<=13),and next K lines, each line contains 2 integers x y means the position of the treasures, x means row and start from 0, y means column start from 0 too.
Output
For each test case, you should output only a number means the minimum cost.
Sample Input
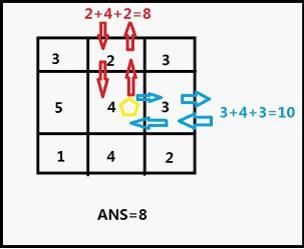
2 3 3 3 2 3 5 4 3 1 4 2 1 1 1 3 3 3 2 3 5 4 3 1 4 2 2 1 1 2 2
Sample Output
8 11
题意:求从外界拿到所有宝藏并且出去的最小花费。
先用k次SPFA求出每个宝藏到每个点的最短路径,然后dp(i,j)表示宝藏获得的状态为i,位
置在j的最小花费,转移方程就是dp(i,j)=min {dp(i^(1<<j),k)+dis(k,j)}.
坑点:
并没有宝藏拿不到的情况不用考虑;
注意-1的格子。
#include <iostream>
#include <algorithm>
#include <string.h>
#include <stdio.h>
#include <map>
#include <vector>
#include <math.h>
#include <queue>
using namespace std;
#define maxn 211
#define INF 1000000000
int mp[maxn][maxn];
int p[maxn][2];
int n, m, k;
int id (int x, int y) {
return x*m+y;
}
#define move Move
const int move[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
bool legal (int x, int y) {
if (x < 0 || y < 0 || x >= n || y >= m)
return 0;
return 1;
}
int d[22][41111];
bool vis[41111];
void spfa (int s, int pos) {
}
vector <int> all[22];
int Count (int x) {
int ans = 0;
while (x) {
ans += (x&1);
x >>= 1;
}
return ans;
}
void init () {
for (int i = 1; i <= k; i++) {
all[i].clear ();
}
for (int i = 1; i < (1<<k); i++)
all[Count (i)].push_back (i);
return ;
}
struct node {
int u, v, w, next;
}edge[211111];
int head[41111], cnt;
void add_edge (int u, int v, int w) {
edge[cnt].u = u, edge[cnt].v = v, edge[cnt].w = w, edge[cnt].next = head[u], head[u] = cnt++;
return ;
}
int dp[1<<13][13];
int top, num[41111];
bool spfa (int x, int y, int *d) {
int n = n*m;
memset (vis, 0, sizeof vis);
int start = id (x, y);
vis[start] = 1;
d[start] = 0;
queue <int> q;
while (!q.empty ()) q.pop ();
q.push (start);
memset (num, 0, sizeof num);
num[start] = 1;
while (!q.empty ()) {
int u = q.front (); q.pop ();
vis[u] = 0;
for (int i = head[u]; i != -1; i = edge[i].next) {
int v = edge[i].v;
if (d[v]>d[u]+edge[i].w) {
d[v] = d[u]+edge[i].w;
if (!vis[v]) {
vis[v] = 1;
q.push (v);
}
}
}
}
return 1;
}
int main () {
//freopen ("in.txt", "r", stdin);
int t, kase = 0;
scanf ("%d", &t);
while (t--) {
scanf ("%d%d", &n, &m);
memset (head, -1, sizeof head); cnt = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
scanf ("%d", &mp[i][j]);
if (mp[i][j] == -1)
continue;
for (int p = 0; p < 4; p++) {
int x = i+move[p][0], y = j+move[p][1];
if (legal (x, y) && mp[x][y] != -1) {
add_edge (id (x, y), id (i, j), mp[i][j]);
}
}
}
}
scanf ("%d", &k);
memset (d, 0x3f3f3f, sizeof d);
for (int i = 0; i < k; i++) {
scanf ("%d%d", &p[i][0], &p[i][1]);
spfa (p[i][0], p[i][1], d[i]);
}
init ();
memset (dp, 0x3f3f3f, sizeof dp);
for (int i = 0; i < k; i++) {//初始化
int x = p[i][0], y = p[i][1];
int &cur = dp[1<<i][i];
for (int j = 0; j < m; j++) {
cur = min (cur, d[i][id (0, j)]+mp[x][y]);
cur = min (cur, d[i][id (n-1, j)]+mp[x][y]);
}
for (int j = 0; j < n; j++) {
cur = min (cur, d[i][id (j, 0)]+mp[x][y]);
cur = min (cur, d[i][id (j, m-1)]+mp[x][y]);
}
}
for (int tt = 2; tt <= k; tt++) {
int Max = all[tt].size ();
for (int pos = 0; pos < Max; pos++) {
int i = all[tt][pos];
for (int j = 0; j < k; j++) if (i&(1<<j)) {
for (int l = 0; l < k; l++) if ((i^(1<<j))&(1<<l)) {
dp[i][j] = min (dp[i][j],
dp[i^(1<<j)][l]+d[l][id(p[j][0], p[j][1])]);
}
}
}
}
int ans = INF;
for (int i = 0; i < k; i++) {
int cur = INF;
int x = p[i][0], y = p[i][1];
for (int j = 0; j < m; j++) {
cur = min (cur, dp[(1<<k)-1][i]+d[i][id(0, j)]);
cur = min (cur, dp[(1<<k)-1][i]+d[i][id(n-1, j)]);
}
for (int j = 0; j < n; j++) {
cur = min (cur, dp[(1<<k)-1][i]+d[i][id(j, 0)]);
cur = min (cur, dp[(1<<k)-1][i]+d[i][id(j, m-1)]);
}
ans = min (ans, cur);
}
printf ("%d\n", ans);
}
return 0;
}