pongo（csdn英雄会）题解之最小操作数---leetcode之word ladder2

这道题今年暑假在家的时候做过，但是超时了，昨天又重新做了下，由于没写注释，拿出以前写的代码，基本看不懂，以后码代码还是要多写注释和文档，下面是题目：

给了A、B两个单词和一个单词集合Dict，每个的长度都相同。我们希望通过若干次操作把单词A变成单词B，每次操作可以改变单词中的一个字母，同时，新产生的单词必须是在给定的单词集合Dict中。求所有行得通步数最少的修改方法。    举个例子如下： Given:    A = "hit"    B = "cog"    Dict = ["hot","dot","dog","lot","log"] Return  [    ["hit","hot","dot","dog","cog"],    ["hit","hot","lot","log","cog"]  ]     即把字符串A = "hit"转变成字符串B = "cog"，有以下两种可能： "hit" -> "hot" ->  "dot" ->  "dog" -> "cog"； "hit" ->  "hot" ->  "lot" ->  "log"  ->"cog"。

-------------------------------------------分割线-----------------------------------------

1.思路：

这道题是不是跟求最短路径有点神似，那么方法就是广度优先搜索BFS，这是图论的知识，显然广度优先搜索需要用到邻接矩阵或者是邻接表（～！我就知道这两种），在此我选择邻接表，因为在BFS图的时候，邻接表在查找邻接关系时较邻接矩阵容易。

那么这道题的解题步骤就是：1）构建邻接表；2）BFS，并对A通往B的路径做标记；3）遍历2）中的路径。

2.解释：

（1）在构建邻接链表的时候，我采用的是头插法；

（2）BFS时，我采用的是以B作为起点，向A搜索，即以目的字符串为起点，这样做我是为了易于返回路径；

（3）对A通往B的路径做标记，我采用了一个元素为vector的动态数组，即std::vector<size_t>*pointTo=new std::vector<size_t>[dictV.size()];

，数组的索引表明这个点的ID，对应的vector存放的是路径中这个点指向的其他点ID。

（4）遍历路径：其实上面的几步已经将图层次化，遍历所有无非就是通过递归或者栈实现，我采用的是递归程序。

下面是示例：

start="bbdk",end="abcd",dict={"cbck","bbck","bbdd","dcck","bbcd","abdd","dccd","accd"};

下面是上述点的对应的图如下：

邻接表如下：

广度优先搜索后，A通往B的路径标记数组值（为了便于浏览，下图将点ID转换成了字符串）如下：-->后面是路径中指向的点

上面的标记数组对应下面层次化的图：

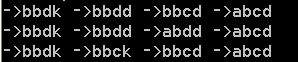
递归遍历 A通往B的所有路径，得到路径：

3.复杂度分析

显然生成邻接表的复杂度是O(n*n*length),BFS和递归寻找路径的复杂度都是O(边数),综上复杂度是O(n*n*length)，是n^2级的，复杂度较高，一种在n很大时降低复杂度的方法见http://blog.csdn.net/caopengcs/article/details/9919341，但是cp修改字母方法来构建邻接表的复杂度我认为应该是O(26*length*n *logn *length)，其中logn是查找map（c++中map的实现是通过树实现的），额外的length是查找map时的字符串比较。

4.代码

#include <string>
#include <vector>
#include <iostream>
#include <set>
//#include <unordered_set>
#include <map>
#include <algorithm>
#include <queue>
#include <stack>
#include <ctime>

using namespace std;
class Node{//用于邻接链表的节点结构
public:
	size_t id;
	Node * next;
	Node(){
		static size_t i=0;
		id=i++;
		next=NULL;
	}
	Node(size_t i,Node* n):id(i),next(n){}
	~Node(){
		if(next){
			delete next;
			next=NULL;
		}
	}
};

class Solution
{
public:
	std::vector<std::string>dictV;
	std::map<std::string,size_t>dictM;
	void findPaths(std::vector<size_t>*pointTo,size_t id,size_t endID,std::vector<std::string>&v,vector<vector<string>>&paths){
		//根据标记数组，递归遍历A到B的所有路径
		if(pointTo[id].at(0)==endID){
			v.push_back(dictV[endID]);
			paths.push_back(v);
		}else{
			for(size_t i=0;i<pointTo[id].size();++i){
				std::vector<std::string>v1(v);
				v1.push_back(dictV[pointTo[id].at(i)]);
				findPaths(pointTo,pointTo[id].at(i),endID,v1,paths);
			}
		}
	}
	bool isOnceDiff(const std::string &str1,const std::string &str2){
       //判断两个字符串是否是仅一个字符不一样
       bool flag=false;
       for(std::string::size_type sst=0;sst<str1.size();sst++){
            if(str1[sst]!=str2[sst]){
                if(!flag)flag=true;
                else {
                    flag=false;
                    break;
                }//else
            }//if
       }//for
       return flag;
   }//isoncediff

    vector<vector<string>> findLadders(string start, string end, set<string> &dict){
		std::vector<std::vector<std::string>> paths;
        if(start==end)return paths;//A==B直接返回
		dict.insert(start);
		dict.insert(end);
		bool *flagHasQued=new bool[dict.size()];//用于BFS的标记
		bool *flagWillQue=new bool[dict.size()];//用于BFS的标记
		size_t num=0;
		for(std::set<std::string>::iterator it=dict.begin();it!=dict.end();it++){
			//为了使用字符串的索引，引入map和vector
			dictV.push_back(*it);
			dictM.insert(make_pair(*it,num));
			flagHasQued[num]=false;
			flagWillQue[num]=false;
			num++;
		}

		//双层循环构建邻接表
		Node *graph=new Node[dict.size()];//
		for(size_t i=0;i<dictV.size();++i){
			for(size_t j=i+1;j<dictV.size();++j){
				if(isOnceDiff(dictV[i],dictV[j])){
					graph[i].next=new Node(j,graph[i].next);
					graph[j].next=new Node(i,graph[j].next);
				}
			}
		}

		//BFS
		std::vector<size_t>*pointTo=new std::vector<size_t>[dictV.size()];
		std::queue<size_t> *que1=new std::queue<size_t>,*que2=new std::queue<size_t>;
		size_t startID=dictM[start];
		size_t endID=dictM[end];
		size_t tmpID=endID;
		que1->push(tmpID);
		flagHasQued[tmpID]=true;
		bool hasArrive=false;
		while(!que1->empty()){//		
			tmpID=que1->front();
			que1->pop();//出队
			Node *tmpNode=graph[tmpID].next;//
			while(tmpNode){
				if(!hasArrive){//这一层第一个找到start的前几个还是添加了指向，这些其实没必要
					if(!flagHasQued[tmpNode->id])
						pointTo[tmpNode->id].push_back(tmpID);
					if(tmpNode->id==startID){
						hasArrive=true;
						break;
					}//if
					if(!flagWillQue[tmpNode->id]){
						que2->push(tmpNode->id);		
						flagWillQue[tmpNode->id]=true;
					}//if
				}else{
					if(tmpNode->id==startID){
						pointTo[tmpNode->id].push_back(tmpID);
						break;
					}
				}//else
				tmpNode=tmpNode->next;
			}//while
			if(hasArrive)
				continue;		
			if(que1->empty()){
				while(!que2->empty()){
					que1->push(que2->front());
					flagHasQued[que2->front()]=true;
					que2->pop();
				}//while
			}//if
		}//while
		if(!hasArrive)
			return paths;

		//递归遍历所有路径
		std::vector<string>path;
		path.push_back(start);
		findPaths(pointTo,startID,endID,path,paths);
		return paths;    
    }
};


//start 提示：自动阅卷起始唯一标识，请勿删除或增加。
int main()
{   
    //

	char* a[]={"cbck","bbck","bbdd","akkd","bbcd","abdd","abkd","accd"};
	std::string start("bbdk");
	std::string end("abcd");
	
	vector<vector<string>> res;
	std::set<string>dict;
	for(int i=0;i<sizeof(a)/sizeof(char*);i++)
		dict.insert(a[i]);
	for(std::set<std::string>::iterator it=dict.begin();it!=dict.end();it++)
		std::cout<<*it<<" ";
	std::cout<<std::endl;

	Solution s;
	clock_t begT=clock();
	res=s.findLadders(start, end, dict);
	clock_t endT=clock();
    std::cout<<"time spent:"<<(endT-begT)/(1.0*CLOCKS_PER_SEC)<<std::endl;
	//std::cout<<res.size()<<std::endl;
	for(size_t i=0;i<res.size();i++){
		for(size_t j=0;j<res[i].size();++j)
			std::cout<<"->"<<res[i][j]<<" ";
		std::cout<<std::endl;
	}
	//"hot","dot","dog","lot","log";
    return 0;
} 
//end //提示：自动阅卷结束唯一标识，请勿删除或增加

以上代码通过了hero，因为hero只要求3s内，但是leetcode当集合达到3K左右时，就超时了。