外部排序--胜者树与败者树

转自：http://blog.163.com/zhaohai_1988/blog/static/20951008520128510538412

参考：http://blog.csdn.net/whz_zb/article/details/7425152

引子

    前面讲到的google面试题 赛马问题 ，我一直在想，会不会有一种算法能讲得更清楚，更明白呢。后来我发现赛马问题和外部排序之归并排序很相似。赛马问题中由于赛道只能一次赛5匹马，就好比我们要对25匹马进行排序，但是发现计算机内存不够（赛道是赛5匹马的），最多同时只能排序5匹马，所以要用外部排序来解决问题。而败者树这种数据结构常用于提高外部排序的效率。所以这篇文章的目的就是把败者树和胜者树讲清楚。

概念介绍

     胜者树和败者树都是完全二叉树，是树形选择排序的一种变型。每个叶子结点相当于一个选手，每个中间结点相当于一场比赛，每一层相当于一轮比赛。

    不同的是，胜者树的中间结点记录的是胜者的标号；而败者树的中间结点记录的败者的标号。

胜者树与败者树可以在log(n)的时间内找到最值。任何一个叶子结点的值改变后，利用中间结点的信息，还是能够快速地找到最值。在k路归并排序中经常用到。

胜者树

     胜者树的一个优点是，如果一个选手的值改变了，可以很容易地修改这棵胜者树。只需要沿着从该结点到根结点的路径修改这棵二叉树，而不必改变其他比赛的结果。

 

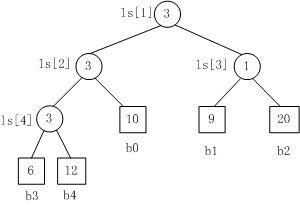
Fig. 1

                                                Fig.1是一个胜者树的示例。规定数值小者胜。

1. b3 PK b4，b3胜b4负，内部结点ls[4]的值为3；
2. b3 PK b0，b3胜b0负，内部结点ls[2]的值为3；
3. b1 PK b2，b1胜b2负，内部结点ls[3]的值为1；
4. b3 PK b1，b3胜b1负，内部结点ls[1]的值为3。

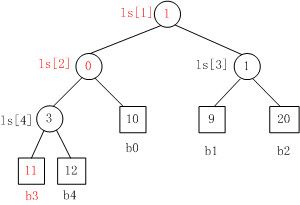
当Fig. 1中叶子结点b3的值变为11时，重构的胜者树如Fig. 2所示。

1. b3 PK b4，b3胜b4负，内部结点ls[4]的值为3；
2. b3 PK b0，b0胜b3负，内部结点ls[2]的值为0；
3. b1 PK b2，b1胜b2负，内部结点ls[3]的值为1；
4. b0 PK b1，b1胜b0负，内部结点ls[1]的值为1。.

Fig. 2

败者树

     败者树是胜者树的一种变体。在败者树中，用父结点记录其左右子结点进行比赛的败者，而让胜者参加下一轮的比赛。败者树的根结点记录的是败者，需要加一个结点来记录整个比赛的胜利者。采用败者树可以简化重构的过程。

 

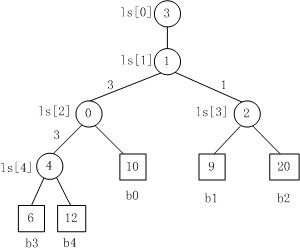
Fig. 3

                                                 Fig. 3是一棵败者树。规定数大者败。

1. b3 PK b4，b3胜b4负，内部结点ls[4]的值为4；
2. b3 PK b0，b3胜b0负，内部结点ls[2]的值为0；
3. b1 PK b2，b1胜b2负，内部结点ls[3]的值为2；
4. b3 PK b1，b3胜b1负，内部结点ls[1]的值为1；
5. 在根结点ls[1]上又加了一个结点ls[0]=3，记录的最后的胜者。

败者树重构过程如下：

• 将新进入选择树的结点与其父结点进行比赛：将败者存放在父结点中；而胜者再与上一级的父结点比较。
• 比赛沿着到根结点的路径不断进行，直到ls[1]处。把败者存放在结点ls[1]中，胜者存放在ls[0]中。

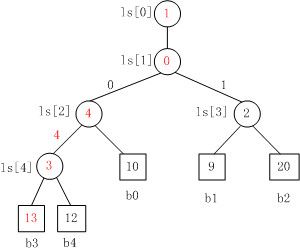
Fig. 4

                                                  Fig. 4是当b3变为13时，败者树的重构图。

 

       注意，败者树的重构跟胜者树是不一样的，败者树的重构只需要与其父结点比较。对照Fig. 3来看，b3与结点ls[4]的原值比较，ls[4]中存放的原值是结点4，即b3与b4比较，b3负b4胜，则修改ls[4]的值为结点3。同理，以此类推，沿着根结点不断比赛，直至结束。

 

败者树和胜者树的区别     

       由上可知，败者树简化了重构。败者树的重构只是与该结点的父结点的记录有关，而胜者树的重构还与该结点的兄弟结点有关。所以败者树常用语外部归并排序。

重要批注

      文章写到这里，我突然发现，败者树还真不能解决赛马问题。为什么这么说呢？因为在赛马问题中，可以同时比较5匹马，选出最快的。而在败者树中，是每次同时比较两个数，选其中的较小值。也就是说，如果赛马问题变换成这样:有5组马，每组有5匹马，并且每组的马按照速度快慢排列好。现在只有一个2跑道的马场，现在要将总共这25匹马按照速度排序。 这个问题才是败者树可以解决的。嘿嘿，描述的问题其实就是外部归并排序了。5组排好序的马，就是5个数组，按照大小排序好。

胜者树和败者树的应用

      贴一道题： 给定一个数组array，长度为16。如何采用最少的比较次数找出第二大的元素？

1. 直观方法是通过两次冒泡排序，15+14=29 次比较可找到第二大的元素。然而直观方法显然没有应用到一些已经比较过的信息。

2. 采用归并排序，构造胜者树。与该胜者比较过的元素有4个（大概就是胜者树的高度），只需要对这些元素进行比较即可，共比较次数15（胜者树）+ （4-1）=18 次比较。

注：也就是说胜者树在求数组最大值，次大值得时候，有用武之地。

 

      败者树在外排序的k路平衡归并中使用，它是一个完全二叉树，其非叶节点（中间节点）为比较中的败者。根节点为最后一次比较的败者。最终胜利者则被直接输出（或到输出缓冲区）。

      败者树的引入是因为：k路平衡归并中，若不使用败者树，则对每次对k路需要比较k-1次得到最值，对于总共n个记录的每一趟归并共需要(n-1)*(k-1)次比较。若有m个归并初始段，归并趟数为logk(m) ,总共比较次数logk(m)*(n-1)*(k-1)。引入败者树（由k个元素构造成败者树）则每次不需要k-1次比较，只需要log2（k）次即可。