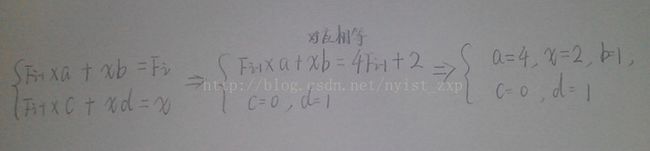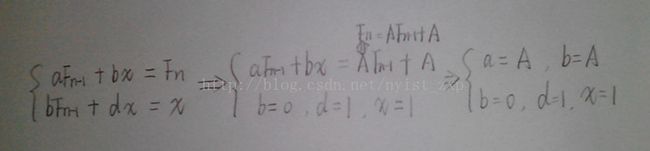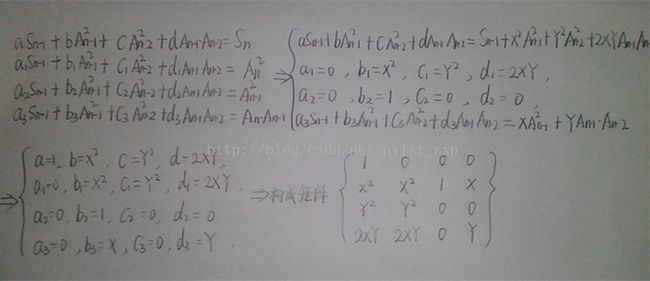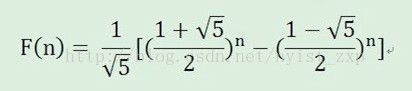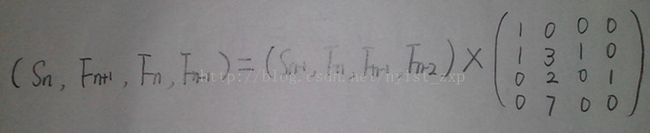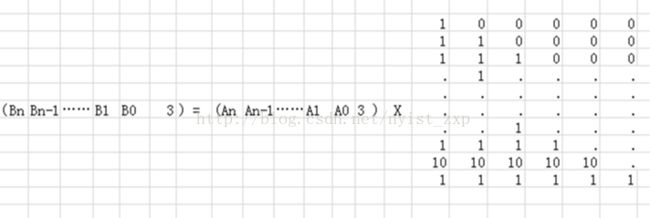矩阵快速幂总结
学习矩阵相乘是由于某星期天在做Bestcoder 的时候第二题就是一个要用矩阵快速幂的题,结果没有做出来,于是就找了几个矩阵相乘的题目做了一下(持续更新中……)。
一 、HDU 4990 Reading comprehension
做题感悟:自从做了这题才发现原来可以这样,于是就开始研究关于矩阵相乘的题目。
解题思路:首先如果你打印前几项你会发现: 1 , 2, 5 ,10 ,21 ,42 ,170 ,如果把奇数项和偶数项分开就会得到通项公式,F[ n ] = 4*F[ n - 1 ] + 2 (偶数项) ,F[n] = 4*F[n-1] + 1 (奇数项) ,其实只要用一个通项公式就可以了,假设我们用偶数项的通项公式求第 n个值 即:n为偶数--> F[n/2] ,n ---> 为奇数项-->F[n/2]*2 + 1 ,好了通项公式已经浮出水面。
接下来就是构造矩阵了,因为右边只有两项所以需要 2 * 2 的矩阵,那么必定是这样构造 ( Fi , x) = (Fi-1 , x) * A( 其中x为常数 ,A为矩阵)同时设 A = {a ,b ,c ,d } ,这样一相乘
就得到各个数:
这样就得到矩阵A了。
代码~~>
做题感悟:开始时推公式推错了推出--> F[ n ] = A * F[ n - 1 ] + 1 ,也没去验证一下就高高兴兴的写代码了,写完才发现原来递推公式不对。。。
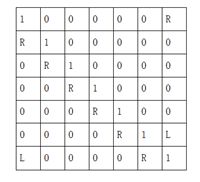
解题思路:方法一、推出上面那个公式完全按照进制类似的思想推的,很明显F[ 2 ] 就不满足,S = A + A ^ 2 + A ^ 3 +……A ^ k = ( ( ( ( A ) * A + A ) * A + A ) * A + A…… ) ,由此得出递推公式--> F[ n ] = A * F[ n - 1 ] + A ;这样第一步完成。
第二步,构造特殊矩阵 B,这里B矩阵同样是 2 * 2 的( 因为右边有两项 ),那么 ( F[ n ] , x ) = ( F[ n - 1 ] , x ) * B , B = { a , b , c , d } ,接下来再来一张自制图片(手机像素有限,就凑合着看吧!) ,A 为输入的矩阵,1为单位矩阵。
方法二、二分
和矩阵快速幂一样,这样二分不用构造矩阵。
1、k 为偶数,设 k = 2*m ,则 S = A + A^2 + A^3 + ……+A^m + (A + A^2 + A^3 + A^4 + A^m) * A^m , b = A^m ,sum = S + S*b ;
2、k为奇数,设 k = 2*m + 1 ;则 S = A + A^2 + A^3 + ……A^m + (A + A^2 + A^3 + ……+ A^m )*A^m + A^k ,b = A^(m+1) ,sum = S + b + S*b ;
代码1~~>
代码2~~>
做题感悟:做完这题就再也不用担心这类题了。。。
解题思路:
第一步:我们还是先推递推公式,因为S[ n ] = S[ n -1 ] + ( An ) ^ 2 { 因为 ( An ) ^ 2 = ( x * An-1 ) ^ 2 + ( y * An-2 ) ^ 2 + 2 * x * y * An-1 * An-2 } = S [ n - 1] + ( x * An-1 ) ^ 2 + ( y * An-2 ) ^ 2 + 2 * x * y * An-1 * An-2 ;
接下来,这样我们构成矩阵相乘的形式:( S[ n ] , ( An ) ^ 2 , ( An-1 ) ^ 2 , An * An-1 ) = (S[ n - 1 ] , ( An-1 ) ^ 2 ,( An-2 ) ^ 2 , An-1 * An-2 ) * B( 4 * 4 的矩阵) ,再看下面的图片~~>
初始矩阵( s1 , A0 ^ 2 , A1 ^ 2 , A0 * A1 ) = ( 2 , 1 , 1 , 1 ) , 注意取余!!
代码~~>
四 、HDU 3117 Fibonacci Numbers
做题感悟:做这题顺便又做了两个关于求位数的题(这里~~>),感觉有学到了一些东西。
解题思路:
这题后四位好求直接矩阵快速幂就 ok 了,重点就是求前四位,Fibonacci 有一个直接求第 n 项的公式 F[ n ] = ( ( ( 1 + sqrt(5)) / 2 ) ^ n - ( ( 1 - sqrt( 5 ) ) / 2 ) ^ n ) / sqrt( 5 ) ; 当 n 大于39 时 ( (1 - sqrt( 5 ) ) / 2 ) ^ n 可以忽略不计了,于是F[ n ] = ( ( ( 1 + sqrt( 5 ) ) / 2 ) ^ n ) / sqrt( 5 ) ; 我们假设 F[ n ] = t * 10 ^ k ,( t为小于1的小数),那么log10( t * 10 ^ k ) = log10( ( ( ( 1 + sqrt( 5 ) ) / 2 ) ^ n ) / sqrt( 5 ) ).
化简一下 ==> log10( t ) + k = n * log10( (1.0 + sqrt( 5.0 ) ) / 2 ) - log10( sqrt( 5.0 ) ) { 令 :temp = n * log10 ( ( 1.0 + sqrt( 5.0 ) ) / 2 ) - log10( sqrt ( 5.0 ) ) , k = ( int ) log10( F[ n ] ) +1 } ==>log 10 ( t ) = temp - k ; 那么 t = 10 ^( log10( t ) ) ,只要将 t * 1000 就可以了。
代码~~>
五 、HDU 4920 Matrix multiplication
做题感悟:做完这题又更加坚信了一点-->一些题要找准突破点,然后从突破点入手,也可以说成从出题人的角度入手。
解题思路:
读完这题,你毕定对题中对 3 取模很诧异,如果用普通的方法 n^3 超时,so~> 需要对 3 下手。
注意到:Ci ,j = Ai * B j ( A , B ,代表向量 ) ,即: A 的第 i 行向量与 B 的第 j 列向量的点积,考虑向量 X 与向量 Y 的点积 ,X * Y = ∑xi*yi ; 只有四种非零项:1*1 ,1*2 ,2*1 ,2*2 ,预处理X ,Y 中1和2的位置(采用 bitset ),每次只要统计两个 bitset 交集的大小。
代码~~>
六 、HDU 4965 Fast Matrix Calculation
做题感悟:这题比赛的时候都没看,看了估计也想不出这种方法,线性代数学的确实不咋的。
解题思路:
看到 C ^ ( n * n ) 就应该想到矩阵快速幂,怎样快速幂呢 ? 暴力明显姿势太难看 ,那就需要想一下优化 ,这里的突破口是 6 ,一般矩阵相乘都需要很小的矩阵,如果太大必定超时,so~> 要用到线性代数 (A*B) ^n = A * ( B * A ) ^ n * B ,这样 B * A ,显然是一个最大 6 * 6 的矩阵完全可以接受。这样复杂度为:O( n * k ^ 2 + k ^ 3 *logn + n * k ^ 2).
代码~~>
七 、HDU 2855 Fibonacci Check-up
做题感悟:深切体会到这种题应该打一下表找一下规律的,因为 n <= 10^9 ,这种一定是推公式然后矩阵快速幂。
解题思路: S[ n ] = F[ n*2 ] (注意 n = 0) ;
代码~~>
八 、HDU 2604 Queuing
解题思路:先说一下自己的思路---> 开始自己深搜了一下打了一个表,于是乎发现了规律 F [ i ] = F[ i - 1 ] + F[ i - 3 ] + F[ i - 4 ] ,然后构造矩阵就傻了,只要添上一项就可以,见图: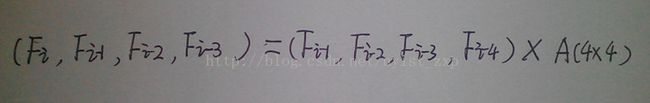
做完后看了一下别人的题解:竟然可以打表,自己怎么就没想到呢?打表要用char的数组,要不然超内存。
某大牛的解释:假设长度为L的队列中存在的序列个数为f(L),那么考虑最后一个放的字母,假设最后一个放m,那么前L-1个可以随意排列,即个数为f(L - 1);如果最后一个放f,那么考虑后两个字母,可能出现的情况为ff,mf,这样比较难判断是否符合题目要求的,所以我们考虑后三个字母,可能出现的情况就为fff,mff,fmf,mmf,显而易见mff,mmf符合题意。当后三个为mmf时,前L-3个可以随意排列,即个数为f(L - 3),当为mff时,可能出现不满足题意的情况,所以我们考虑后四个字母,可能出现的情况为mmff,fmff,只有mmff满足题意,即个数为f(L - 4)。因此可以得到一个递推式f(L) = f(L - 1) + f(L - 3) + f(L - 4)。那么剩下的就是矩阵快速幂的任务了。
打表代码~~>
代码~~>
九 、HDU 1757 A Simple Math Problem
裸的矩阵快速幂,公式已经给出,构造 10*10 的矩阵即可,代码~~> ;
十 、HDU 2256 Problem of Precision
解题思路:这题感觉很有档次,矩阵快速幂里面只能是整数,因为要对某个数取模。
代码~~>
十一、坐标点的变换
平面中一个点绕另一个点旋转θ弧度公式:
(逆时针): x = ( x1 - x0 ) * cos( θ ) - ( y1 - y0 ) * sin( θ ) + x0 ;
y = ( x1 - x0 ) * sin( θ ) + ( y1 - y0 ) * cos( θ ) + y0 ;
(顺时针):只需要用π*2 - θ 就好。
摘自Matrix67
给定n个点,m个操作,构造O(m+n)的算法输出m个操作后各点的位置。操作有平移、缩放、翻转和旋转 , 这里的操作是对所有点同时进行的。其中翻转是以坐标轴为对称轴进行翻转(两种情况),旋转则以原点为中心。如果对每个点分别进行模拟,那么m个操作总共耗时O(mn)。利用矩阵乘法可以在O(m)的时间里把所有操作合并为一个矩阵,然后每个点与该矩阵相乘即可直接得出最终该点的位置,总共耗时O(m+n)。假设初始时某个点的坐标为x和y,下面5个矩阵可以分别对其进行平移、旋转、翻转和旋转操作。预先把所有m个操作所对应的矩阵全部乘起来,再乘以(x,y,1),即可一步得出最终点的位置。
注意如果输入角度的话需要转换为弧度(1弧度 = 180/π 度 ,1度 = π / 180 弧度)
NYOJ 298 点的变换
十二、 给定一个有向图,问从一点恰好走 K 步(允许重复走),到达另一点的方法数(mod p)。
建立邻接矩阵,m[ i ][ j ] = 1 (表示从 i 点到 j 点存在一条路),G[ i ][ j ] = Σ m[i][k] * m[k][j] ,枚举中间点计算总的路径数,相当于Floyed一样,平方相当于走两步所得到的方法数,K 次方就相当于走K步的方法数。
NYOJ 530 K steps 裸题
NYOJ 302 星际旅行 这个需要处理一下图,就可以了。
代码~~>
十三、循环矩阵问题。
有一些题的矩阵可以推出第一行,然后由第一行推出余下的所有行,见下图:
除了最左边的等于上一行的最后一个元素外,m[ i ][ j ] = m[ i - 1 ] [ j - 1 ] ;这样只需要求出第一行的元素,然后递推剩余的行就可以。这样矩阵的复杂度从O( n^3 )降到了O( n^2 )
FZU 1692 Key problem
每一个数更新后只与前一个数的值后一个数值和原先的值相关,于是只要 Ai = L*a( i - 1 + n )%n + ai + R * a( i + 1)%n ,这样在构造矩阵的时候 左边的数的系数是L,右边的数的系数是R,本身的系数是 1 ,其余的都是 0 。
代码~~>
NYOJ 300 Kiki & Little Kiki 2 思路和上面的差不多。
公式:Fibonacci 前 n 项和公式 S[ n ] = F[ n + 2 ] - 1 ;
十四、ZOJ 3538 Arrange the Schedule
做题感悟:这题很好,需要分段处理,开始想的太简单了以为大多数是 3 ,结果果断 WA。
解题思路:
这题需要分段处理,一段一段的,还要分两种情况,两边的字符相同时是一种情况,不相同时是一种情况,但是递推公式是一样的。
递推公式: F[ n ] = 2 * F[ n - 1 ] + 3 * F[ n - 2 ] .or F[ n ] = 3^n - F[ n - 1 ] ;
注意:如果给定的出题是不合法的需要输出0 。
代码~~>
代码~~>
十五、FZUOJ 1683 纪念SlingShot
做题感悟:很简单的一题,开始自己用五维的递推式写的,然后看了别人的竟然可以用四维,但是自己推四维的时候,nc了一会才推出来。
解题思路:
不再解释直接上图:
代码~~>
十六、POJ 3420 Quad Tiling
做题感悟:这题推公式推的真心痛,开始以为只和倒数第一行和倒数第二行有关,结果列了一个二元一次方程,很明显不对,接着列三个方程,还是不对,差点晕倒,推了一会基本确定第 n - 1 和第 n - 2 行的系数,然后就猜了一下第 n - 3 行和第 n - 4 行的系就搞定了。发现不会 DP 真的很无语。
解题思路:
直接上递推方程 : dp [ n ] = dp[ n - 1 ] + 5 * dp[ n - 2 ] + dp[ n - 3 ] - dp [ n - 4 ] ; 有了方程之后构造出矩阵就ok了。
代码~~>
十七、HDU 5015 233 Matrix
做题感悟:比赛时各种推规律,各种搞,但是依然没有搞定,学了矩阵快速幂之后,发现TMD就是一水题。
解题思路:
一看题需要取模,m 很大 ,n 很小,很明显矩阵快速幂。已经给出递推公式:ai,j = ai-1,j + ai,j-1( i , j ≠ 0) .
矩阵构造如下:
代码~~>
十八、HDU 4686 Arc of Dream
做题感悟:简单题,和 Fibonacci 求前 n 项和一样,推一下就好。
注意:取模的时候要特别注意,还有就是很坑的一点 n = 0 的时候输出 0 。
代码~~>
十九、HDU 5068 Harry And Math Teacher
矩阵快速幂+线段树:题解
Reference resources and good blogs about matrix :
Matrix67
ffjjqqjj
hrdv