POJ 2049
Finding Nemo
| Time Limit: 2000MS | Memory Limit: 30000K | |
| Total Submissions: 6978 | Accepted: 1592 |
Description
Nemo is a naughty boy. One day he went into the deep sea all by himself. Unfortunately, he became lost and couldn't find his way home. Therefore, he sent a signal to his father, Marlin, to ask for help.
After checking the map, Marlin found that the sea is like a labyrinth with walls and doors. All the walls are parallel to the X-axis or to the Y-axis. The thickness of the walls are assumed to be zero.
All the doors are opened on the walls and have a length of 1. Marlin cannot go through a wall unless there is a door on the wall. Because going through a door is dangerous (there may be some virulent medusas near the doors), Marlin wants to go through as few doors as he could to find Nemo.
Figure-1 shows an example of the labyrinth and the path Marlin went through to find Nemo.
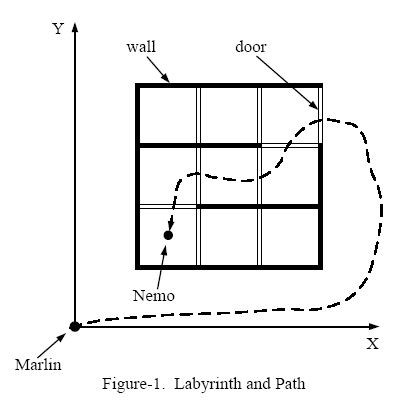
We assume Marlin's initial position is at (0, 0). Given the position of Nemo and the configuration of walls and doors, please write a program to calculate the minimum number of doors Marlin has to go through in order to reach Nemo.
After checking the map, Marlin found that the sea is like a labyrinth with walls and doors. All the walls are parallel to the X-axis or to the Y-axis. The thickness of the walls are assumed to be zero.
All the doors are opened on the walls and have a length of 1. Marlin cannot go through a wall unless there is a door on the wall. Because going through a door is dangerous (there may be some virulent medusas near the doors), Marlin wants to go through as few doors as he could to find Nemo.
Figure-1 shows an example of the labyrinth and the path Marlin went through to find Nemo.

We assume Marlin's initial position is at (0, 0). Given the position of Nemo and the configuration of walls and doors, please write a program to calculate the minimum number of doors Marlin has to go through in order to reach Nemo.
Input
The input consists of several test cases. Each test case is started by two non-negative integers M and N. M represents the number of walls in the labyrinth and N represents the number of doors.
Then follow M lines, each containing four integers that describe a wall in the following format:
x y d t
(x, y) indicates the lower-left point of the wall, d is the direction of the wall -- 0 means it's parallel to the X-axis and 1 means that it's parallel to the Y-axis, and t gives the length of the wall.
The coordinates of two ends of any wall will be in the range of [1,199].
Then there are N lines that give the description of the doors:
x y d
x, y, d have the same meaning as the walls. As the doors have fixed length of 1, t is omitted.
The last line of each case contains two positive float numbers:
f1 f2
(f1, f2) gives the position of Nemo. And it will not lie within any wall or door.
A test case of M = -1 and N = -1 indicates the end of input, and should not be processed.
Then follow M lines, each containing four integers that describe a wall in the following format:
x y d t
(x, y) indicates the lower-left point of the wall, d is the direction of the wall -- 0 means it's parallel to the X-axis and 1 means that it's parallel to the Y-axis, and t gives the length of the wall.
The coordinates of two ends of any wall will be in the range of [1,199].
Then there are N lines that give the description of the doors:
x y d
x, y, d have the same meaning as the walls. As the doors have fixed length of 1, t is omitted.
The last line of each case contains two positive float numbers:
f1 f2
(f1, f2) gives the position of Nemo. And it will not lie within any wall or door.
A test case of M = -1 and N = -1 indicates the end of input, and should not be processed.
Output
For each test case, in a separate line, please output the minimum number of doors Marlin has to go through in order to rescue his son. If he can't reach Nemo, output -1.
Sample Input
8 9 1 1 1 3 2 1 1 3 3 1 1 3 4 1 1 3 1 1 0 3 1 2 0 3 1 3 0 3 1 4 0 3 2 1 1 2 2 1 2 3 1 3 1 1 3 2 1 3 3 1 1 2 0 3 3 0 4 3 1 1.5 1.5 4 0 1 1 0 1 1 1 1 1 2 1 1 1 1 2 0 1 1.5 1.7 -1 -1
Sample Output
5 -1
Source
Beijing 2004
故事背景很有意思的一道题,一开始不会处理边的情况,后来才发现可以把边缩到他左下的那个点;
网上有一种用优先队列的BFS,学习了。
PS:INF不能开到INT_MAX,会爆int的。
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <cstring>
#include <map>
#include <string>
#include <stack>
#include <cctype>
#include <vector>
#include <queue>
#include <set>
using namespace std;
//#define Online_Judge
#define outstars cout << "***********************" << endl;
#define clr(a,b) memset(a,b,sizeof(a))
#define FOR(i , x , n) for(int i = (x) ; i < (n) ; i++)
#define FORR(i , x , n) for(int i = (x) ; i <= (n) ; i++)
#define REP(i , x , n) for(int i = (x) ; i > (n) ; i--)
#define REPP(i ,x , n) for(int i = (x) ; i >= (n) ; i--)
const int MAXN = 200 + 5;
const int maxw = 100 + 20;
const int MAXNNODE = 1000000 +10;
const long long LLMAX = 0x7fffffffffffffffLL;
const long long LLMIN = 0x8000000000000000LL;
const int INF = 9999999;
const int IMIN = 0x80000000;
#define eps 1e-8
#define mod 1000000007
typedef long long LL;
const double PI = acos(-1.0);
typedef double D;
typedef pair<int , int> pi;
struct node
{
int x , y , len;
bool operator < (const node & a)const
{
return len > a.len;
}
};
int n , sx , m , sy ,xmax , ymax;
int h[MAXN][MAXN] , l[MAXN][MAXN] , dis[MAXN][MAXN];
priority_queue <node> q;
void bfs()
{
int x , y;
FORR(x , 0 , xmax)
{
FORR(y , 0 , ymax)
{
dis[x][y] = INF;
}
}
while(!q.empty())q.pop();
node pn;
pn.x = 0;
pn.y = 0;
pn.len = 0;
dis[0][0] = 0;
q.push(pn);
while(!q.empty())
{
pn = q.top();
q.pop();
x = pn.x , y = pn.y;
if(x == sx&&y == sy)return ;
if(y + 1 <= ymax&&dis[x][y + 1] > dis[x][y] + h[x][y + 1])
{
dis[x][y + 1] = dis[x][y] + h[x][y + 1];
pn.x = x ;
pn.y = y + 1;
pn.len = dis[x][y + 1];
q.push(pn);
}
if(y - 1 >= 0&&dis[x][y -1] > dis[x][y] + h[x][y])
{
dis[x][y - 1] = dis[x][y] + h[x][y];
pn.x = x ;
pn.y = y - 1;
pn.len = dis[x][y - 1];
q.push(pn);
}
if(x - 1 >= 0&&dis[x - 1][y] > dis[x][y] + l[x][y])
{
dis[x - 1][y] = dis[x][y] + l[x][y];
pn.x = x - 1 ;
pn.y = y;
pn.len = dis[x - 1][y];
q.push(pn);
}
if(x + 1 <= xmax&&dis[x + 1][y] > dis[x][y] + l[x + 1][y])
{
dis[x + 1][y] = dis[x][y] + l[x + 1][y];
pn.x = x + 1 ;
pn.y = y;
pn.len = dis[x + 1][y];
q.push(pn);
}
}
dis[sx][sy] = -1;
}
int main()
{
//ios::sync_with_stdio(false);
#ifdef Online_Judge
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif // Online_Judge
int x , y , d , t ;
double tx , ty;
while(scanf("%d%d" , &n , &m) == 2)
{
if(m == -1&&n == -1)break;
xmax = ymax = -1;
clr(h , 0), clr(l , 0);
FOR(i , 0 , n)
{
scanf("%d%d%d%d" , &x , &y , &d , &t);
if(d == 0)
{
FOR(j , 0 , t)
{
h[x + j][y] = INF;
}
xmax = max(xmax , x + t);
ymax = max(ymax , y);
}
else
{
FOR(j , 0 ,t)
{
l[x][y + j] = INF;
}
xmax = max(xmax , x);
ymax = max(ymax , y + t);
}
}
FOR(i , 0 , m)
{
scanf("%d%d%d" , &x , &y ,&d);
if(d == 0)h[x][y] = 1;
else l[x][y] = 1;
}
scanf("%lf%lf" , &tx ,&ty);
if(tx > xmax||ty > ymax)
{
printf("0\n");
}
else
{
sx = (int)tx;
sy = (int)ty;
bfs();
printf("%d\n" , dis[sx][sy]);
}
}
return 0;
}