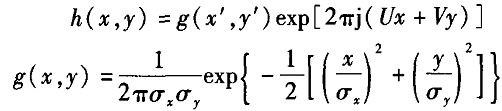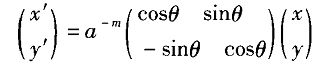基于Gabor滤波器的纹理分割
Gabor变换是一种短时傅里叶变换方法,其实质是在傅里叶变换中加入一个窗函数,通过窗函数来实现信号的时频分析。当选取高斯函数作为窗函数时,短时傅里叶变换称为Gabor变换。在一维情况中,Gabor变换代表着时频分析的最优方法,二维情况中则是空间频域分析的方法。对于图像来说,窗函数决定了它在空域的局部性,所以可以通过移动窗口的中心來获得不同位置的空间域信息。由于髙斯函数在经过傅里叶变换以后仍然是高斯函数,这就使得Gabor变换在频域上仍然是局部的。简直完美!
与传统的傅立叶变换相比,Gabor小波变换具有良好的时频局部化特性。即非常容易地调整Gabor滤波器的方向、基频带宽及中心频率从而能够最好的兼顾信号在时空域和频域中的分辨能力;Gabor小波变换具有多分辨率特性即变焦能力;采用多通道滤波技术,将一组具有不同时频域特性的Gabor小波应用于图像变换,每个通道都能够得到输入图像的某种局部特性,这样可以根据需要在不同粗细粒度上分析图像。
Gabor滤波器纹理分析方法是一种重要的基于变换的纹理特征提取方法,通过选用某一特定的Gabor函数,设计Gabor滤波器,来实现图像的多尺度、多方向的特征提取。
gabor滤波器的参数很多,看着就让人头晕,搞清楚各个参数的物理含义及相互之间的关系后,公式就好理解了。后面使用的话设好参数就可以直接用。
标准差σx、σy分别为高斯函数沿 x 轴和 y 轴的标方差, 控制高斯窗口作用的范围,σx、σy越大,高斯窗作用的范围也越大。变换σx、σy可以使gabor滤波器匹配图像中不同空间尺度的结构。通常取σx=σy。
这里的纵横比y/x=1。关于纵横比说一下,纵横比控制高斯函数横截面的椭圆形状,为1时截面就是圆。
(U,V)是中心频率,其频率调制的方向角φ=arctan(V/U)。
对高斯基本函数g(x,y)进行尺度变换和旋转变换得到一簇自相似函数,即Gabor小波,这样gabor滤波器就可以在不同尺度、方向上分析纹理,粗糙的纹理用低分辨率分析,细致的纹理用高分辨率去分析。其中尺度变换和旋转函数如下
θ 表示空域坐标绕x轴逆时针旋转θ 角,对θ 离散化, 令θ=n*π /N ,n= 0,1, N-1,N 为整数.则可用n定义滤波器的方向。改变θ,滤波器就可以在不同方向上检测纹理。a为伸缩因子,a>1,一般取a=1.414,m 定义滤波器的尺度,m=1,2,...M-1。
通常情况下,取Gabor函数中高斯函数部分的方向θ与复数调制部分函数的辐角φ相等,即令θ=φ。
令
![]()
则gabor函数可化简为
定义波长(λ):λ是COS调制因子的波长,它的值以像素为单位指定,通常大于等于2.但不能大于输入图像尺寸的五分之一。 λ和F有如下关系:
λ=2*π/F
要实现多尺度检测的话,要么改变波长,要么改变中心频率,滤波器的中心频率越小(即波长越长),提取的纹理特征的尺度越大。当滤波器纹理与图像作用时,滤波器覆盖下的局部纹理频率与滤波器的频率越接近响应就越大,反之越小。
φ是cos调制因子的相位偏移值,φ决定了Gabor函数的对称性,比如在φ=0,π的时候,Gabor函数是中心(对于(U,V)来说)对称的,而当 φ=-π/2,π/2的时候,Gabor函数是中心反对称的,并且所有其他情况都是这两种情况的组合。
gabor函数可以表示为一个椭圆高斯函数与一个复平面函数的乘积形式。复数形式的二维 gabor函数包含两个正交投影: 实数的偶对称余弦部分和虚数的奇对称正弦部分。一般根据需要提取实数部分或虚数部分或复数幅值。
#ifndef __GABOR__
#define __GABOR__
class gabor
{
//#define PI 3.1415926
typedef unsigned char BYTE;
const double phase=0;//相位The phase offset φ in the
//argument of the cosine factor of the Gabor function is specified in degrees
//const double gama=1.8;//纵横比
const double OriBandwidth = PI / 6;//Orientation Bandwidth of a Gabor filter
const double FreBandwidth = 1;
//const int kernel_size = 21;
const double bandwidth = 1;
const int theta_bins = 8;const int img_size = 256;
private:
//void resize256();//如果最长边大于256,则将图像按比例缩放到256*,为了减小运算量
void get_kernel(double*&kernel,const double theta,const double lamda,int &kernel_w,int&kernel_h);
//void low_pass_filter();
//double calculateSigma(double waveLength, double bandwidth);
void filter2D(double*kernel, const int kernel_w, const int kernel_h,
BYTE*img,const int img_w,const int img_h,double**&out,int cnt);
public:
gabor();
~gabor();
void apply_filter(BYTE*grey_img,const int imgH,const int imgW,double**&output);
};
#endif
#include "stdafx.h"
#include "gabor.h"
#include<cmath>
gabor::gabor()
{
}
gabor::~gabor()
{
}
//double gabor::gabor_func(BYTE*Image, const int imgH, const int imgW, const double oriBand,
// const double theta, const double lambda, const double phi, const double freBand)
//{
// //determine Sx and Sy by Oritation Frequency and Bandwidth Bandwidth
// double Sx = lambda / PI*sqrt(log(2) / 2)*((pow(freBand,2) + 1) / (pow(freBand,2) - 1));
// double Sy = lambda / PI* sqrt(log(2) / 2) / tan(oriBand / 2);
//
//}
void gabor::apply_filter(BYTE*grey_img, const int imgH, const int imgW, double**&output)
{
int lamda_n = (log(img_size / 8.0) + 0.01) / log(2.0);
double*lamda=new double[lamda_n];//The wavelength of the cosine factor of the Gabor filter
for (int i = 0; i < lamda_n; i++)
{
lamda[i] = 2 * pow(sqrt(2.0), double(i));
printf("%lf ", lamda[i]);
}
double*kernel = NULL;
double*theta = new double[theta_bins];//The orientation of Gabor filter
for (int i = 0; i < theta_bins; i++)
theta[i] = double(i) / theta_bins*PI;
output = new double*[imgH * imgW];
for (int i = 0; i < imgH*imgW; i++)
{
output[i] = new double[theta_bins * lamda_n];
}
for (int i = 0; i < lamda_n; i++)
for (int j = 0; j < theta_bins; j++)
{
int kernel_w=0, kernel_h=0;
get_kernel(kernel,theta[j], lamda[i], kernel_w, kernel_h);
filter2D(kernel, kernel_w, kernel_h, grey_img, img_size, img_size, output, i * 6 + j);
delete[]kernel;
kernel = NULL;
}
delete[]lamda,theta;
}
void gabor::get_kernel(double*&kernel, const double theta, const double lamda, int &kernel_w, int&kernel_h)
{
double Sx = lamda / PI*sqrt(log(2) / 2)*((pow(2, FreBandwidth) + 1) / (pow(2 ,FreBandwidth) - 1));
double Sy = lamda / PI* sqrt(log(2) / 2) / tan(OriBandwidth / 2);
double Sigma_max = Sx; if (Sy>Sx)Sigma_max=Sy;
//Gabor Mask Size
kernel_w = ceil(Sigma_max * 3) * 2 + 1;
kernel_h = ceil(Sigma_max * 3) * 2 + 1;
if (kernel)
delete[]kernel;
kernel = new double[kernel_w*kernel_w];
for (int m = 0; m < kernel_h;m++)
for (int n = 0; n < kernel_w; n++)
{
int x = m - ceil(kernel_w / 2);
int y = n - ceil(kernel_h / 2);
double xPrime = x * cos(theta) + y * sin(theta);
double yPrime = y * cos(theta) - x * sin(theta);
kernel[m*kernel_w + n] = 1 / (2 * PI*Sx*Sy)*exp(-0.5*(pow(xPrime / Sx, 2.0)
+ (yPrime / Sy)*(yPrime / Sy)))*cos(2 * PI*xPrime / lamda + phase);
//printf("%lf ", kernel[m*kernel_w + n]);
}
//printf("\n");
}
void gabor::filter2D(double*kernel, const int kernel_w, const int kernel_h, BYTE*img,
const int img_w, const int img_h, double**&out, int chanel)
{
BYTE*img_data = new BYTE[img_h*img_w];
for (int i = 0; i < img_h; i++)
for (int j = 0; j < img_w; j++)
{
double temp = 0;
int cnt = 0;
for (int m = -kernel_h/2; m <= kernel_h/2; m++)
for (int n = -kernel_w/2; n <= kernel_w/2; n++)
{
double img_value = (i + m >= 0 && i + m < img_h
&&j + n >= 0 && j + n < img_w) ? img[(i + m)*img_w + j + n] : 0;
temp += img_value*kernel[cnt++];
}
out[i*img_w + j][chanel] = abs(temp);
img_data[i*img_w + j] = abs(50*temp);
}
/*save_gray("11.bmp", img_data, img_h, img_w);
CxImage cx;
cx.Load("11.bmp", CXIMAGE_FORMAT_BMP);
int templates[25] = { 1, 4, 7, 4, 1,
4, 16, 26, 16, 4,
7, 26, 41, 26, 7,
4, 16, 26, 16, 4,
1, 4, 7, 4, 1 };
cx.Filter(templates, 25, 273, 0);*/
delete[]img_data;
return ;
}
opencv里的gabor核函数生成代码
/*
Gabor filters and such. To be greatly extended to have full texture analysis.
For the formulas and the explanation of the parameters see:
http://en.wikipedia.org/wiki/Gabor_filter
*/
cv::Mat cv::getGaborKernel( Size ksize, double sigma, double theta,
double lambd, double gamma, double psi, int ktype )
{
double sigma_x = sigma;
double sigma_y = sigma/gamma;
int nstds = 3;
int xmin, xmax, ymin, ymax;
double c = cos(theta), s = sin(theta);
if( ksize.width > 0 )
xmax = ksize.width/2;
else
xmax = cvRound(std::max(fabs(nstds*sigma_x*c), fabs(nstds*sigma_y*s)));
if( ksize.height > 0 )
ymax = ksize.height/2;
else
ymax = cvRound(std::max(fabs(nstds*sigma_x*s), fabs(nstds*sigma_y*c)));
xmin = -xmax;
ymin = -ymax;
CV_Assert( ktype == CV_32F || ktype == CV_64F );
Mat kernel(ymax - ymin + 1, xmax - xmin + 1, ktype);
double scale = 1;
double ex = -0.5/(sigma_x*sigma_x);
double ey = -0.5/(sigma_y*sigma_y);
double cscale = CV_PI*2/lambd;
for( int y = ymin; y <= ymax; y++ )
for( int x = xmin; x <= xmax; x++ )
{
double xr = x*c + y*s;
double yr = -x*s + y*c;
double v = scale*exp(ex*xr*xr + ey*yr*yr)*cos(cscale*xr + psi);
if( ktype == CV_32F )
kernel.at<float>(ymax - y, xmax - x) = (float)v;
else
kernel.at<double>(ymax - y, xmax - x) = v;
}
return kernel;
}
分割步骤
对待分割图像F(m,n)进行多尺度、多方向的Gabor变换。
对得到的各子带采用非线性变换函数进行变换,并通过低通滤波来降低相同纹理区域内特征的变换,增加不同区域的区别。
将上述处理得的各子带对应的像素组成向量
采用分类算法对特征向量进行分类,实现纹理图像的分割。
Log Gabor