SPOJ BYTESE1 - spfa(最短路+搜索)

Description

LUCIUS’ DUNGEON (5 points) There are a set of rooms in a dungeon, arranged in an M × N rectangular grid. In one of the rooms, evil Lucius Malfoy has imprisoned Hermione, owing to his hatred towards the mudbloods. The noble Harry potter is on his way to rescue Hermione. Harry potter starts in the room at the top left corner of the grid, which is labeled (1,1). Each room contains some guards. It takes some time for Harry potter to kill all the guards in the room he is in. The time taken to kill the guards varies from room to room. Once he has killed all the guards in a room, he can move on to any one of its neighbors by going left, right, up or down, provided, of course, that there is a neighboring room in the corresponding direction. He cannot move diagonally.
Lucius Malfoy, knowing that Harry Potter is on his way, has set a time bomb that will kill Hermione after T seconds. You will be given the position of Hermione, the time left for the bomb to go off and the time it takes for Harry to kill the guards in each of the rooms in the dungeon. Your task is to determine if it is possible for Harry to reach Hermione and save her by defusing the bomb before the T seconds expire. For example, suppose the dungeon is described by the following grid of numbers where the numbers start from (1,1):
2 3 2
2 5 1
5 3 1
3 1 1
The number at position (i,j) indicates the time taken for Harry Potter to overpower the guards in room (i,j). Suppose Hermione is in the room at position (4,2). If T = 10. There is no way Harry Potter can reach Hermione in time. However, if M = 15, Harry Potter can reach Hermione with 4 seconds to spare, as follows. Starting from (1,1), he moves right to (1,2) and then (1,3), comes down all the way to (4,3) and then moves to (4,2). This takes 11 seconds (note that he must also overpower the guard in the room where Hermione is incarcerated). You can check that he cannot reach Hermione with more than 4 seconds to spare by any route.
Note: If Harry reaches Hermione at exactly ‘T’ seconds from the start then the answer is “YES” with 0 seconds to spare.

Input

The first line consists of the number of test cases K (1<=K<=20). In each test case, the first line contains two integers M and N indicating the number of rows and columns in the rectangular dungeon(1 ≤ M,N≤ 100). Next M lines contain N integers (single digits only). The jth integer on ith line is the time taken to overpower the guards at room (i,j). The last line in each test case, contains three integers a, b and T, where (a,b) is the position of the cell where Hermione is held and T is the amount of time before the bomb goes off.

Output

For each of the test case, if it is not possible for Harry Potter to save Hermione then print NO. Otherwise, print two lines. The first line should say YES. The second line should contain a single integer indicating the maximum possible time to spare when Harry Potter rescues the Hermione.

Sample Input

Input:
2
4 3 
2 3 2
2 5 1
5 3 1
3 1 1
4 2 15
2 2
1 2
1 1
2 2 2

Output:
YES
4
NO

题意：从（1， 1）点出发，到（a, b），要是所用的时间小于给定的T，那么输出YES，并且输出T - ans（剩下多少时间）

                                                                                                                                   （二）

Description

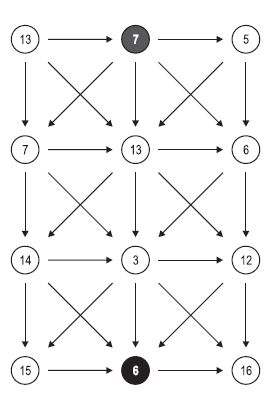
Here’s a simple graph problem: Find the shortest path from the top-middle vertex to the bottom-middle vertex in a given tri-graph. A tri-graph is an acyclic graph of (N ≥ 2) rows and exactly 3 columns. Unlike regular graphs, the costs in a tri-graph are associated with the vertices rather than the edges.

So, considering the example with N = 4, the cost of going straight down from the top to bottom along the middle vertices is 7 + 13 + 3 + 6 = 29. The layout of the directional edges in the graph are always the same as illustrated in the figure.

Input

Your program will be tested on one or more test cases.
Each test case is specified using N + 1 lines where the first line specifies a single integer (2 ≤ N ≤ 100, 000) denoting the number of rows in the graph. N lines follow, each specifying three integers representing the cost of the vertices on the ith row from left to right. The square of each cost value is less than 1,000,000.
The last case is followed by a line with a single zero.

Output

For each test case, print the following line:
k. n
Where k is the test case number (starting at one,) and n is the least cost to go from the top-middle vertex to the bottom-middle vertex.

Example

Input:
4
13 7 5
7 13 6
14 3 12
15 6 16
0

Output:
1. 22

给出n * 3 矩阵，要求计算从第一行第二个数到最后一行第二个数的最短路.........

共有3列

发现这两个题的代码是一样的

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <queue> 
using namespace std;

#define MX 110
int r, c;
int a, b;
int g[MX][MX], dis[MX][MX];
bool vis[MX][MX];
int d[4][2] = {0, 1, 0, -1, 1, 0, -1, 0};

queue< pair<int, int> > Q;

int spfa() {
	memset(dis, 0x3f, sizeof(dis));
	memset(vis, 0, sizeof(vis));
	Q.push(make_pair(1, 1));
	vis[1][1] = 1;
	dis[1][1] = g[1][1];
	while(!Q.empty()) {
		pair<int, int> t = Q.front();
		Q.pop();
		int x = t.first;
		int y = t.second;
		vis[x][y] = 0;
		for(int i = 0; i < 4; ++i) {
			int X = x + d[i][0];
			int Y = y + d[i][1];
			if(X >= 1 && Y >= 1 && X <= r && Y <= c && dis[X][Y] > dis[x][y] + g[X][Y]) {
				dis[X][Y] = dis[x][y] + g[X][Y];
				if(X == a && Y == b) continue;
				if(!vis[X][Y]) {
					vis[X][Y] = 1;
					Q.push(make_pair(X, Y));
				}
			}
		}
	}
	return dis[a][b];
}

int main() {
	int T;
	scanf("%d", &T);
	while(T--) {
		
		scanf("%d%d", &r, &c);
		for(int i = 1; i <= r; ++i) {
			for(int j = 1; j <= c; ++j) {
				scanf("%d", &g[i][j]);
			}
		}
		int T;
		scanf("%d%d%d", &a, &b, &T);
		int ans = spfa();
	//	printf("%d\n", ans);
		if(ans <= T) printf("YES\n%d\n", T - ans);
		else printf("NO\n");
	} 	
	return 0;
} 

（2）

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <queue> 
using namespace std;

#define MX 100100
int r, c;
int a, b;
int g[MX][5], dis[MX][5];
bool vis[MX][5];
int d[4][2] = {-1,1,0,1,1,1,1,0};

queue< pair<int, int> > Q;

int spfa() {
	memset(dis, 0x3f, sizeof(dis));
	memset(vis, 0, sizeof(vis));
	Q.push(make_pair(1, 2));
	vis[1][2] = 1;
	dis[1][2] = g[1][2];
	while(!Q.empty()) {
		pair<int, int> t = Q.front();
		Q.pop();
		int x = t.first;
		int y = t.second;
		vis[x][y] = 0;
		for(int i = 0; i < 4; ++i) {
			int X = x + d[i][1];
			int Y = y + d[i][0];
			if(X >= 1 && Y >= 1 && X <= r && Y <= 3 && dis[X][Y] > dis[x][y] + g[X][Y]) {
				dis[X][Y] = dis[x][y] + g[X][Y];
				if(X == a && Y == b) continue;
				if(!vis[X][Y]) {
					vis[X][Y] = 1;
					Q.push(make_pair(X, Y));
				}
			}
		}
	}
	return dis[a][b];
}

int main() {
	int T, k;
	k=1;
	while(~scanf("%d",&r)&&r){
		
		for(int i = 1; i <= r; ++i) {
			for(int j = 1; j <= 3; ++j) {
				scanf("%d", &g[i][j]);
			}
		}
		a=r;
		b=2;
		int ans = spfa();

		printf("%d. %d\n",k++,ans);
	
	} 	
	return 0;
}