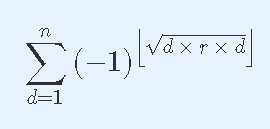【清华集训2014】【BZOJ3817】Sum

Description

给定正整数N，R。求

Input

第一行一个数 T，表示有 T 组测试数据。
接下来 T 行，每行两个正整数 n,r。
Output

输出 T 行，每行一个整数表示答案。
Sample Input

3

3 5

3 6

3 7
Sample Output

3

1

-1
HINT

对于 100% 的数据，满足 n≤10^9,r≤10^4,T≤10^4。

Source

2015年国家集训队测试

我们令 x=r√ ,则所求

∑d=1n(−1)⌊dx⌋

注意到 (−1)⌊dx⌋=(−1)⌊d(2−x)⌋
因此x>2甚至x>1都是无意义的.

首先如果r是完全平方数,那么可以直接得出答案.
不是完全平方也没关系,我们只要知道有多少 ⌊dx⌋ 为奇数或偶数(随便选择一个来求)就行了
这里我们基于偶数来做.
已知 ⌊dx⌋ 为偶数当且仅当满足条件 2⌊dx2⌋=⌊dx⌋
那么问题就可以转化为求

∑d=1n(4⌊dx2⌋−2⌊dx⌋+1)

即为

n+4∑d=1n⌊dx2⌋−2∑d=1n⌊dx⌋

将求和全部看成

∑d=0n⌊bx+ca⌋

的形式.
然后可以用类欧几里得算法来递归求解.

关于类欧几里得..我以后有时间了可能单独写一篇文章..?

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define GET (ch>='0'&&ch<='9')
#define LL long long
using namespace std;
int T,n,r,t;
double R;
void in(int &x)
{
    char ch=getchar();x=0;
    while (!GET)    ch=getchar();
    while (GET) x=x*10+ch-'0',ch=getchar();
}
int gcd(int a,int b)    {   return !b?a:gcd(b,a%b); }
int calc(int n,int a,int b,int c)
{
    if (!n) return 0;
    int Gcd=gcd(a,gcd(b,c));a/=Gcd;b/=Gcd;c/=Gcd;
    LL m=((LL)b*R+c)/a,sum=(LL)n*(n+1)/2*m;
    c-=m*a;m=((LL)b*R+c)/a*n;sum+=n*m;
    return sum-calc(m,b*b*r-c*c,a*b,-a*c);
}
int main()
{
    for (in(T);T;T--)
    {
        in(n);in(r);R=sqrt(r);t=(int)(R);
        if (t*t==r) printf("%d\n",t&1?(n&1?-1:0):n);
        else    printf("%d\n",n-((calc(n,1,1,0)-(calc(n,2,1,0)<<1))<<1));
    }
}