最长不降子序列 LIS(Longest Increasing Subsequence) 动态规划与深度搜索

看清楚题意， 再做题。 我发现我总是给自己出题， 把题目的意思看成另一个， 哎， 结果又来一套说法.

这是我做poj 1836 Alignment， 繁衍出的. 注意:以下跟poj 1836题意不一。

最长不降子序列

例题: 下面给出三组数,第一行一个队列是人数， 然后队伍各自的身高， 问从中抽出多少个人可以让剩下的人员从左至右是低到高。

input:

5

1 1 1 1 1

7
1.7 1.5 1.3 1.3 1.5 1.6 1.7

7

1 7 3 5 9 4 8

output:

0

2

3

这个问题比较简单， 但是我想通过这个问题的不断变形重写，加深理解深度优先及动态规划， 熟悉各种写法

下面程序的应该是属于深度优先, 它没有状态转移方程， 无最优子结构:

1. 这个由于用mina 存储着最终结果， 这个就不需要return；没有返回值，那也不适合存储中间结果.

 因为是前面的结果作用于后面， 存储中间结果你会发现没有必要， 而且也不好改写成有返回值的函数

#include "iostream"
using namespace std;
int n; 
double a[1010], mina, maxHeight[1002];	

void ok(int i, int num){	            //i是当前人的编号， num是之前剔除的人数
	if(i == n){
		if(maxHeight[n - 1] > a[n])		//maxHeight[i]代表编号i之前的人留下来的最大身高
			num++;
		if(mina > num)
			mina = num;
		return;
	}
	else if(i < n){
		if(maxHeight[i - 1] <= a[i]){	//比上一组最高的人高， 不踢除当前此人
			maxHeight[i] = a[i];		//最高的人变为此人身高
			ok(i+1, num);		        //排除的人数不增加
		}
		maxHeight[i] = maxHeight[i-1];	//当前此人高度比上一个低或高, 都可能抽出此人
		ok(i+1, num+1);		        	//进入下一个人， 提出的人数加1
		
	}
}

int main(){
    while(cin>>n){						//队伍的人数
		int i;
		memset(maxHeight, 0, sizeof(maxHeight));
		for(i = 1; i <= n; i++)
			cin>>a[i];
		mina = 999999.0;
		maxHeight[0] = 0;
		ok(1, 0);
		cout<<mina<<endl;
	}
	return 0;
}

我们改变一下ok函数的参数， 可以让maxHeight数组就用一个maxHeight变量代替, 对程序经常变形， 熟悉各种方式对于写程序,看别人的程序是很有好处的，起到忽略形式， 注重思想的作用

#include "iostream"
using namespace std;

int n; 
double a[1010], mina;	

void ok(int i, int num, double maxHeight){	          //i是当前人的编号， num是之前剔除的人数
	if(i == n + 1){			                  //判断条件可以更改一下
		if(mina > num)
			mina = num;
		return;
	}
	else if(i <= n){
		if(a[i] >= maxHeight)
			ok(i+1, num, a[i]);
		ok(i+1, num+1, maxHeight);
	}
}

int main(){
    while(cin>>n){						//队伍的人数
		int i;
		for(i = 1; i <= n; i++)
			cin>>a[i];
		mina = 999999.0;
		ok(1, 0, 0);
		cout<<mina<<endl;
	}
	return 0;
}

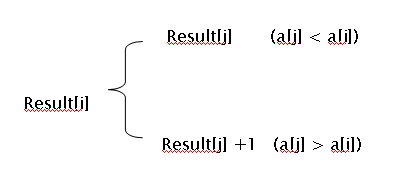
一开始改成动态规划的时候想建立

这样的动态转移方程， 但是result[j]之前的选择对于result[i]的选择有影响， 因为 a[j]不是最高的一个， 这不满足无后效性

在根据无后效性确定状态，

根据最优子结构确定    状态转移方程 result[i] = result[j] + i - j - 1;

再写动态规划的程序
result[i]为 1 到 编号i 要踢出的最少人， j 比 i 矮，      (i - j - 1)是 j 到 i 之间要踢出的人

因为最后一个人也就是n, 可能不选他， 所以应该从n+1算起， 第一个人你也可能不选， 所以我们到0结束。

当然略微更改一下程序也可以改头尾结束编号

程序: (自顶向下)

#include "iostream"  
using namespace std;  
#define maxNum 9999999
int n, result[1010];   
double a[1010], mina;   
  
int ok(int i){   
	if(result[i] != -1)
		return result[i];
	if(i == 0)
		return 0;
	int min = maxNum, j;
	for(j = i-1; j >= 0; j--){
		if(a[j] <= a[i]){
			int temp = ok(j) + i - j - 1;
			if(temp < min)
				min = temp;
		}
	}
	result[i] = min;
	return min;
}  
  
int main(){  
    while(cin>>n){  
        int i;  
        for(i = 1; i <= n; i++)  
            cin>>a[i];  
		memset(result, -1, sizeof(result));
		a[0] = 0;
		a[n+1] = maxNum;
        cout<<ok(n + 1)<<endl; 
    }  
    return 0;  
}  

自下而上的程序

#include "iostream"    
using namespace std;    

#define maxNum 9999999  
int n, result[1010];     
double a[1010]; 

int main(){    
    while(cin>>n){    
        int i, j, cost;    
        for(i = 1; i <= n; i++)    
            cin>>a[i];    
        memset(result, -1, sizeof(result));  
		
		a[0] = 0;
		result[0] = 0;
        for(i = 1; i <= n; i++){    
            int min = 0xfffffff;    
            for(j = 0; j < i; j++){    
				if(a[j] <= a[i]){
					cost = result[j] + i - j - 1;     
					min = min > cost ? cost: min;    				
				}
            }    
			result[i] = min;
        }    
        cout<<result[n]<<endl;   
    }    
    return 0;    
}  

自顶向下的记忆化方式和 自底向上的方式

自顶向下的记忆化方式只不过是动态程序设计的一种变形， 动态程序的执行方式是自底向上， 所有子问题计算一次， 充分利用迭代子问题，

另外， 他无需递归代价， 其维护及仪表的开销也要小一些， 因此其效率好于自顶向下 --<<实用算法的分析与程序设计>>