hdu4341(分组背包)
Gold miner
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1444 Accepted Submission(s): 575
Problem Description
Homelesser likes playing Gold miners in class. He has to pay much attention to the teacher to avoid being noticed. So he always lose the game. After losing many times, he wants your help.
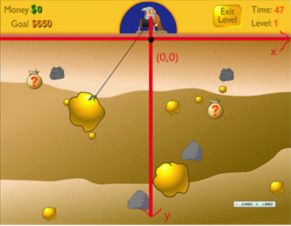
To make it easy, the gold becomes a point (with the area of 0). You are given each gold's position, the time spent to get this gold, and the value of this gold. Maybe some pieces of gold are co-line, you can only get these pieces in order. You can assume it can turn to any direction immediately.
Please help Homelesser get the maximum value.

To make it easy, the gold becomes a point (with the area of 0). You are given each gold's position, the time spent to get this gold, and the value of this gold. Maybe some pieces of gold are co-line, you can only get these pieces in order. You can assume it can turn to any direction immediately.
Please help Homelesser get the maximum value.
Input
There are multiple cases.
In each case, the first line contains two integers N (the number of pieces of gold), T (the total time). (0<N≤200, 0≤T≤40000)
In each of the next N lines, there four integers x, y (the position of the gold), t (the time to get this gold), v (the value of this gold). (0≤|x|≤200, 0<y≤200,0<t≤200, 0≤v≤200)
In each case, the first line contains two integers N (the number of pieces of gold), T (the total time). (0<N≤200, 0≤T≤40000)
In each of the next N lines, there four integers x, y (the position of the gold), t (the time to get this gold), v (the value of this gold). (0≤|x|≤200, 0<y≤200,0<t≤200, 0≤v≤200)
Output
Print the case number and the maximum value for each test case.
Sample Input
3 10 1 1 1 1 2 2 2 2 1 3 15 9 3 10 1 1 13 1 2 2 2 2 1 3 4 7
Sample Output
Case 1: 3 Case 2: 7
Author
HIT
Source
2012 Multi-University Training Contest 5
本题要求在给定时间下尽可能多的找到金子,
同一方向是有先后顺序的,不同方向可以任意转换。
同一方向是有先后顺序的,不同方向可以任意转换,我们的在这句话上挖掘有用信息,及同一方向不能跳跃。若我们把同一方向的时间、价值累加,就形成了等价且数目相同的互斥事件,即在同一方向上只能取一个。统计出不同方向数、每个方向事件数结合规定时间T,就可以找到对应的模型-分组背包。即把物品分组,每组内只能取一个(不能同时取多个),状态转移方程为:
dp[k][j]=max(dp[k-1][j],dp[k-1][j-t[i]]+v[i]),i属于小组k
for 所有的组k
for v=V..0
for 所有的i属于组k
f[v]=max{f[v],f[v-c[i]]+w[i]}
对于本题,怎么分组呢?由于是从原点出发,所以很快就能想到应按斜率分组(大小顺序任选),在斜率相同即属于同一组时按据原点距离从小到大排序(这点很重要-因为我们要累加同一方向时间、价值的)。
#include<iostream> #include<algorithm> #include<cstdio> using namespace std; struct node { int x,y,t,val; }Point[200+20]; int num,tim; int group[200*2+20][200+10]; int dp[40000+100]; int cnt; bool cmp(node a,node b)//在题目明确给出的条件下此函数即可保证先按斜率从小到大,再按距离远点距离从小到大排序 { if(a.x*b.y!=a.y*b.x) return a.y*b.x<a.x*b.y; return a.y<b.y; } int Max(int a,int b) { return a<b?b:a; } void GroupPack() { int i,j,k; memset(dp,0,sizeof(dp)); for(i=0;i<cnt;i++) { //printf("********%d\n",group[i][0]); for(j=tim;j>=0;j--) { for(k=1;k<=group[i][0];k++) { if(j>=Point[group[i][k]].t) dp[j]=Max(dp[j],dp[j-Point[group[i][k]].t]+Point[group[i][k]].val); } } } } int main() { int i,tag=1; while(~scanf("%d%d",&num,&tim)) { for(i=0;i<num;i++) scanf("%d%d%d%d",&Point[i].x,&Point[i].y,&Point[i].t,&Point[i].val); sort(Point,Point+num,cmp); cnt=0; for(i=0;i<num;i++) { group[cnt][0]=0; group[cnt][++group[cnt][0]]=i; for(i++;i<num;i++) { if(Point[i].x*Point[i-1].y==Point[i-1].x*Point[i].y) { Point[i].val+=Point[i-1].val; Point[i].t+=Point[i-1].t; group[cnt][++group[cnt][0]]=i; } else { i--; break; } } cnt++; } GroupPack(); printf("Case %d: %d\n",tag++,dp[tim]); } return 0; }