如何利用堆栈及逆波兰表达式进行数学四则运算(C语言版)
本文演示如何利用自定义堆栈(可实现通用性)和逆波兰表达式(后缀表达式)来进行数学四则运算。
阅读须知:了解堆栈定义过程、了解中缀表达式、了解后缀表达式(逆波兰表达式)。不清楚的同学百度一下,用10分钟了解一下即可。
示例程序优点:
1,自己做了一些注释, 尽量将转换原理和计算原理说清一些,如果还有看不明白的同学,只好移步百度谷歌了。
2,自己定义了一个堆栈,可实现数据类型无关性。简称通用性堆栈。参考文章:http://www.2cto.com/kf/201108/98664.html
3,基于以上两点,以后大家如需将中缀表达式转换为后缀表达式或者需使用通用性堆栈,可直接使用示例中的源码。
缺点:
1,代码没做什么优化,对用户输入也没有严格验证。
注:做一个利用堆栈及逆波兰表达式进行数学四则运算的小程序,一方面方便自己以后查看使用。另一方面,也希望抛砖引玉,大家一起来探寻更好的计算方法。
附源码:
calc3.c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define TRUE 1
#define FALSE 0
#define ERROR -1
#define STACKELEMENT 100 //定义堆栈中可入栈元素个数
#define BUFFERSIZE 100 //定义临时缓冲区大小
typedef int Status; //定义返回状态
typedef struct //定义堆栈:堆栈中只定义栈大小和每次入栈元素大小,栈中一律使用空指针进行操作。这样,我们自己定义的栈就做到了和数据类型无关性。真正实现了栈的通用。
{
void *base; //指向栈底
void *top; //指向栈顶
int stackSize; //栈的空间总容量大小
int typeSize; //入栈时,单个元素占用空间大小
} sqStack;
Status InitStack(sqStack *s,unsigned stackSize,unsigned typeSize); //初始化栈
Status Push(sqStack *s,void *e); //入栈
Status Pop(sqStack *s,void *e); //出栈
Status ClearStack(sqStack *s); //清空栈内所有元素
Status DestroyStack(sqStack *s); //销毁栈
int GetLen(sqStack *s); //获取已入栈元素个数
Status Calculate(char *arr,void *result); //计算表达式结果:参数一:arr为使用空格分隔的采用后缀表达式表示的要计算的字符串,例:arr={"3 5 + "}。参数二:result存放计算结果。
Status InfixToPostfix(char *infix,char *postfix); //将中缀表达式转换为后缀表达式。例:infix={"3+5\n"} ,转换后,postfix={"3 5 + "};
void my_err(char *str); //自定义错误处理函数
int main(int argc,char *argv[])
{
printf("Please input the nifix expression.\n"); //输入中缀表达式。
char src[BUFFERSIZE]={'\0'}; //存放中缀表达式的临时缓冲区
char *infix=src;
char postfix[BUFFERSIZE]={'\0'}; //存放后缀表达式的临时缓冲区
fgets(infix,BUFFERSIZE,stdin); //从标准输入流中读取要计算的四则运算表达式
printf("Infix expression:%s",infix);
InfixToPostfix(infix,postfix); //将中缀转换为后缀表达式
printf("Postfix expression:%s\n",postfix);
double result;
Calculate(postfix,&result); //计算后缀表达式的结果
printf("result:%f\n",result);
exit(0);
}
/*
将中缀表达式转换为后缀表达式
参数:infix 指向中缀表达式,以回车键即\n结尾。
postfix 指向后缀表达式临时缓冲区,用来存放转换后的结果。
附转换规则:从左到右遍历中缀表达式的每个数字和符号,若是数字则直接保存在postfix数组中;若是符号,则判断其与栈顶符号的优先级,是右括号或者优先级不大于栈顶符号,则栈顶元素依次出栈并输出,直到遇到左括号或者栈空时,才将刚才的那个符号入栈。
*/
Status InfixToPostfix(char *infix,char *postfix)
{
sqStack s;
if(InitStack(&s,STACKELEMENT*sizeof(char),sizeof(char))==ERROR)
my_err("InfixToPostfix init stack error!");
char c,e;
int j=0,i=0;
c=*(infix+i); //取出中缀表达式中的第一个字符
i++;
while('\n'!=c) //遇到换行符,表示转换结束
{
while(c>='0'&&c<='9') //先判断一下取出的字符是否是数字,如果是数字的话,则直接存入postfix数组
{
postfix[j++]=c;
c=*(infix+i);
i++;
if(c<'0'||c>'9') //如果不是数字,则在后面添加空格,以便区分各个符号
{
postfix[j++]=' ';
}
}
if(')'==c) //不是数字,则判断是否为右括号。[括号的优先级最高,所以,如果是右括号的话,就得先进行括号里的各种运算]
{
Pop(&s,(void*)&e);
while('('!=e) //直到遇到左括号为止
{
postfix[j++]=e;
postfix[j++]=' ';
Pop(&s,(void*)&e);
}
}
else if('+'==c||'-'==c) //如果是加减号,因为他俩的优先级最低了,所以此时先将栈里的所有符号出栈后(除非遇到左括号),再把此符号入栈
{
if(!GetLen(&s)) //如果是空栈,则直接将加减号入栈
{
Push(&s,(void*)&c);
}
else
{
do
{
Pop(&s,(void*)&e);
if('('==e)
{
Push(&s,(void*)&e);
}
else
{
postfix[j++]=e;
postfix[j++]=' ';
}
}while(GetLen(&s)&&'('!=e); //将栈里的所有符号出栈(除非遇到左括号)
Push(&s,(void*)&c); //最后将新来的加减号再入栈
}
}
else if('*'==c||'/'==c||'('==c) //如果是乘除号或左括号,因为他们的优先级高,所以直接入栈。
{
Push(&s,(void*)&c);
}
else if('\n'==c) //判断一下,所有符号是否都已转换完成
{
break;
}
else //能走到这个else的,都是我不认识的符号了
{
// printf("\nError:input error,the character %d cann't recognize!\n",c);
return -1;
}
c=*(infix+i); //取出下一个字符进行转换
i++;
}
while(GetLen(&s)) //转换完成后,栈里可能还有没出栈的运算符号
{
Pop(&s,(void*)&e);
postfix[j++]=e;
postfix[j++]=' ';
}
DestroyStack(&s);
return TRUE;
}
/*
计算后缀表达式的结果
参数:arr使用空格分隔的后缀表达式字符串。例:arr="31 5 + "
result 保存计算完毕后的结果
注:如何利用栈来计算后缀表达式的结果:依次取出后缀表达式中的符号进行比较,如果是数字,则直接入栈;如果是符号,则出栈两次,弹出两个要计算的因数,进行计算,之后再将计算结果入栈。知道后缀表达式中所有符号都已比较完毕。
*/
Status Calculate(char *arr,void *result)
{
// printf("%s\n",arr);
double d,e,f; //d,e 存放两个因数。f存放d,e计算后的结果.
sqStack s;
char *op; //存放后缀表达式中的每个因数或运算符
char *buf=arr; //声明bufhe saveptr两个变量,是strtok_r函数的需要。
char *saveptr=NULL;
if(InitStack(&s,STACKELEMENT*sizeof(double),sizeof(double))==ERROR)
my_err("Calculate init stack error!");
while((op=strtok_r(buf," ",&saveptr))!=NULL) //利用strtok_r函数分隔字符串
{
buf=NULL;
switch(op[0])
{
case '+':
Pop(&s,&d);
Pop(&s,&e);
f=d+e;
Push(&s,&f);
break;
case '-':
Pop(&s,&d);
Pop(&s,&e);
f=e-d;
Push(&s,&f);
break;
case '*':
Pop(&s,&d);
Pop(&s,&e);
f=d*e;
Push(&s,&f);
break;
case '/':
Pop(&s,&d);
Pop(&s,&e);
f=e/d;
Push(&s,&f);
break;
default:
d=atof(op); //不是运算符,就肯定是因数了。所以,用atof函数,将字符串转换为double类型
Push(&s,&d);
break;
}
}
Pop(&s,result);
DestroyStack(&s);
return TRUE;
}
/*
初始化栈
参数:stackSize:栈的总容量大小
typeSize:以后要入栈的单个元素的大小
*/
Status InitStack(sqStack *s,unsigned stackSize,unsigned typeSize)
{
s->base=malloc(stackSize);
if(!s->base)
return ERROR;
s->top=s->base;
s->stackSize=stackSize;
s->typeSize=typeSize;
return TRUE;
}
/*
压栈
*/
Status Push(sqStack *s,void *e)
{
if((int)s->top-(int)s->base+s->typeSize>s->stackSize)
return FALSE;
memcpy(s->top,e,s->typeSize);
s->top=(void*)((int)s->top+s->typeSize);
return TRUE;
}
/*
出栈
*/
Status Pop(sqStack *s,void *e)
{
if(s->top==s->base)
return FALSE;
s->top=(void*)((int)s->top-(int)s->typeSize);
memcpy(e,s->top,s->typeSize);
return TRUE;
}
/*
清栈
*/
Status ClearStack(sqStack *s)
{
s->top=s->base;
return TRUE;
}
/*
毁栈
*/
Status DestroyStack(sqStack *s)
{
free(s->base);
s->top=s->base=NULL;
s->stackSize=s->typeSize=0;
return TRUE;
}
/*
获取已入栈元素个数
*/
int GetLen(sqStack *s)
{
return ((int)s->top-(int)s->base)/s->typeSize;
}
/*
自定义错误处理函数
*/
void my_err(char *str)
{
perror(str);
exit(1);
}
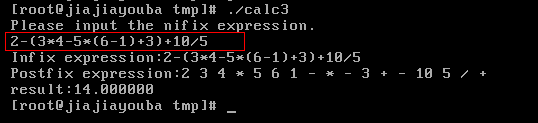
示例运算: