Codeforces 444A DZY Loves Physics(贪心，数学)
题目链接
DZY loves Physics, and he enjoys calculating density.
Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:
where
v is the sum of the values of the nodes,
e is the sum of the values of the edges.
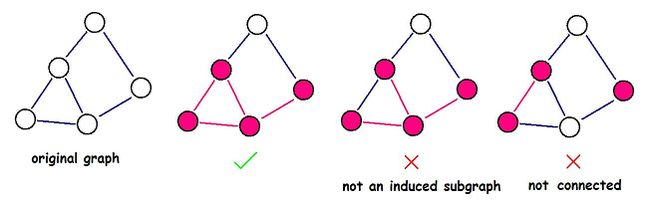
Once DZY got a graph G, now he wants to find a connected induced subgraph G' of the graph, such that the density of G' is as large as possible.
An induced subgraph G'(V', E') of a graph G(V, E) is a graph that satisfies:
; - edge
if and only if 
, and edge 
; - the value of an edge in G' is the same as the value of the corresponding edge in G, so as the value of a node.
Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.
The first line contains two space-separated integers n (1 ≤ n ≤ 500), 
. Integer n represents the number of nodes of the graph G, m represents the number of edges.
The second line contains n space-separated integers xi (1 ≤ xi ≤ 106), where xi represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.
Each of the next m lines contains three space-separated integers ai, bi, ci (1 ≤ ai < bi ≤ n; 1 ≤ ci ≤ 103), denoting an edge between node ai and bi with value ci. The graph won't contain multiple edges.
Output a real number denoting the answer, with an absolute or relative error of at most 10 - 9.
1 0 1
0.000000000000000
2 1 1 2 1 2 1
3.000000000000000
5 6 13 56 73 98 17 1 2 56 1 3 29 1 4 42 2 3 95 2 4 88 3 4 63
2.965517241379311
题意：n个点的无向图。每个点有点权，边有边权。一个图的密度的定义为：
1，顶点只有一个，则密度为0
2，顶点大于1个，密度等于v/e，v为点权和，e为边权和。
求该图的所有子图中，最大的密度值。
题解：可以证明密度最大的子图，一定只有两个点。
假设一个图现在有两个点点权为v1，v2，他们之间相连的边的边权为m1，该图的密度为(v1+v2)/m1。如果增加一个点v3要让该图的密度增加，若v3与v2相连的边的边权为m2。那么只有与v3/m2>(v1+v2)/m1，该图的密度才会增加。但是此时，v2与v3两个点构成的子图的密度为(v2+v3)/m2>(v1+v2+v3)/(m1+m2)。所以密度最大的子图一定只有两个点。
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
#include<string>
#include<stack>
#include<math.h>
#include<vector>
#include<set>
#include<map>
#define nn 110000
#define inff 0x3fffffff
#define eps 1e-8
#define mod 1000000007
typedef long long LL;
const LL inf64=LL(inff)*inff;
using namespace std;
int n,m;
double a[510];
int main()
{
int i;
while(scanf("%d%d",&n,&m)!=EOF)
{
for(i=1;i<=n;i++)
{
scanf("%lf",&a[i]);
}
double ans=0;
int u,v;
double l;
for(i=1;i<=m;i++)
{
scanf("%d%d%lf",&u,&v,&l);
ans=max(ans,(a[u]+a[v])/l);
}
printf("%.10lf\n",ans);
}
return 0;
}