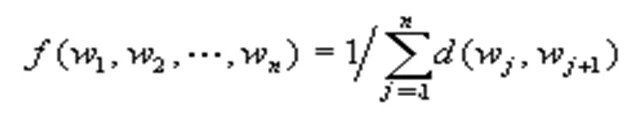遗传算法
关键字:人工智能,遗传算法,进化计算
Production system
Abstract: Genetic algorithm (geneticalgorithms, GA) is mimic biological genetics and natural selection mechanism, the random global search algorithm of adaptive (Holland, Mr Rand) and the nature of "natural selection" and "evolution" Darwin (Charles Darwin) and biological genetic theory (Gregor Johann Mendel in fruit, John Mendel) theory synthetically, through artificial means the constructed a kind of random adaptive global optimization search algorithm, is a kind of mathematical simulation of biological evolution process, is the most important form of evolutionary computation. Genetic algorithm (ga) for those who are hard to find the problem of traditional mathematical model points out a solution. Evolutionary computation and genetic algorithm is used to refer to some knowledge of the biological sciences, this also reflected the characteristics of artificial intelligence in the interdisciplinary. This paper mainly discusses the computer science and technology under the junior in professional class "artificial intelligence" sixth experiment algorithm.
Keywords: Artificial intelligence, genetic algorithms, evolutionary computation
1,编码与译码
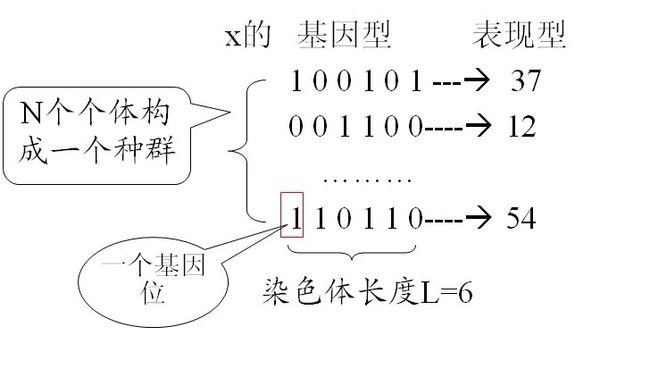
借用生物的术语,把位串形式的解的编码表示叫染色体或基因型(基因表达),或叫个体。原问题结构即一个染色体解码后所对应的解称为表现型。编码空间也称为基因型空间或搜索空间。解空间也称为表现型空间。
进化算法不是直接作用在问题的解空间上,而是交替地作用在编码空间和解空间上。在编码空间对个体进行遗传操作,在解空间对问题的解进行评估。
2,适应度函数
为了体现染色体的适应能力,引入了对问题中的每一个染色体都能进行度量的函数,叫适应度函数。通过适应度函数来决定染色体的优、劣程度,它体现了自然进化中的优胜劣汰原则。对优化问题,适应度函数就是目标函数。TSP的目标是路径总长度为最短,路径总长度的倒数就可以为TSP的适应度函数。
其中wn+1= w1。适应度函数要有效反映每一个染色体与问题的最优解染色体之间的差距,一个染色体与问题的最优解染色体之间的差距小,则对应的适应度函数值之差就小,否则就大。适应度函数的取值大小与求解问题对象的意义有很大的关系。
1)计算各染色体适应度值
2)累计所有染色体适应度值(或选择概率),记录每个个体的适应度累加值(或概率累加值)
3) 产生一个随机数 r,0< r < sumN(或0< r < 1)
4)若sumk-1< r £ sumk(或qk-1< r £ qk ),则选择第k个个体进入交配池。
5) 重复(3)和(4),直到获得足够的染色体。
4,程序流程
一般遗传算法的主要步骤如下:
(1) 随机产生一个由确定长度的特征字符串组成的初始群体。
(2) 对该字符串群体迭代的执行下面的步①和② ,直到满足停止标准:
①计算群体中每个个体字符串的适应值;
②应用选择、交叉和变异等遗传算子产生下一代群体。
(3) 把在后代中出现的最好的个体字符串指定为遗传算法的执行结果,这个结果可以表示问题的一个解。
5,问题解析





6,程序设计
#include<iostream>
#include<cstdlib>
#include<ctime>
#include<cmath>
#include<iomanip>
using namespace std;
const int NUM=1000; //最大迭代次数
const int POP_SIZE=50; //种群规模:个体数量
const int GENE=33; //每个个体染色体个数
const int GB1=18; //染色体手段基因片段(二进制)
const int GB2=15; //染色体末端基因片段(二进制)
const int GD=6; //十进制保留小数点位数
const double PI=3.1415926;
void initialize(int v[][GENE]) //初始化群体
{
int ii,ij;
srand(time(0));
cout<<"基因初始化:"<<endl;
for(ii=0;ii<POP_SIZE;ii++)
{
cout<<endl<<"个体"<<setw(2)<<ii+1<<"基因型 ";
for(ij=0;ij<GENE;ij++)
{
v[ii][ij]=2*rand()/RAND_MAX;
cout<<v[ii][ij];
}
}
cout<<endl;
}
void evaluation(int v[][GENE],double eval[]) //评估函数
{
int ii,ij;
double x1,x2;
for(ii=0;ii<POP_SIZE;ii++)
{
x1=x2=0;
for(ij=0;ij<GB1;ij++) //二进制片段转为十进制编码
{
x1+=v[ii][ij]*pow(2,(GB1-(ij+1)));
}
for(ij=GB1;ij<GENE;ij++)
{
x2+=v[ii][ij]*pow(2,(GENE-(ij+1)));
}
x1=-3.0+x1*(12.1-(-3.0))/(pow(2,GB1)-1); //十进制编码转为十进制值
x2=4.1+x2*(5.8-4.1)/(pow(2,GB2)-1);
eval[ii]=21.5+x1*sin(4*PI*x1)+x2*sin(20*PI*x2);
}
}
int best_eval(double eval[]) //找出每代中最优秀个体基因值
{
int ii,cursor=0;
for(ii=0;ii<POP_SIZE;ii++)
{
if(eval[ii]>eval[cursor])
{
cursor=ii;
}
}
return cursor;
}
int worst_eval(double eval[]) //找出每代中最差个体基因值
{
int ii,cursor=0;
for(ii=0;ii<POP_SIZE;ii++)
{
if(eval[ii]<eval[cursor])
{
cursor=ii;
}
}
return cursor;
}
void selection(double eval[],int v[][GENE],int v_next[][GENE])
{
int ii,ij,ik;
double value;
double p[POP_SIZE]; //选择概率
double pp[POP_SIZE]={0}; //累积概率
double total_value=0;
for(ii=0;ii<POP_SIZE;ii++)
{
total_value+=eval[ii];
}
for(ii=0;ii<POP_SIZE;ii++)
{
p[ii]=eval[ii]/total_value;
}
pp[0]=p[0];
for(ii=1;ii<POP_SIZE;ii++)
{
pp[ii]=pp[ii-1]+p[ii];
}
for(ii=0;ii<POP_SIZE;ii++) //对于每个次代个体的基因型
{
value=(double)rand()/RAND_MAX; //转动轮盘
for(ij=0;ij<POP_SIZE;ij++) //搜索命中区域
{
if(value<pp[ij]) //找到后复制、跳出
{
for(ik=0;ik<GENE;ik++)
{
v_next[ii][ik]=v[ij][ik];
}
break;
}
}
}
}
void crossover(int v[][GENE])
{
int ii,ij,ik;
double p=0.8,value1;
int n=0,tmp,value2;
int cursor[POP_SIZE]={-1}; //被选中的染色体下标
for(ii=0;ii<POP_SIZE;ii++) //找被选中的染色体下标
{
value1=(double)rand()/RAND_MAX;
if(value1<p)
{
cursor[n++]=ii;
}
}
for(ii=0;ii<n;ii+=2) //两两配对,进行交叉
{
value2=(int)(GENE-1)*rand()/RAND_MAX+1;
for(ij=value2;ij<GENE;ij++)
{
tmp=v[cursor[ii]][ij];
v[cursor[ii]][ij]=v[cursor[ii+1]][ij];
v[cursor[ii+1]][ij]=tmp;
}
}
}
void mutation(int v[][GENE])
{
int ii,ij,ik;
int sum,gene; //基因变异数目
double pm=0.01; //变异概率
sum=(int)(POP_SIZE*GENE*pm)+1;
for(ii=0;ii<sum;ii++)
{
gene=(int)(POP_SIZE*GENE)*rand()/RAND_MAX;
ij=gene/(POP_SIZE*GENE);
ik=gene%(POP_SIZE*GENE);
v[ij][ik]=1-v[ij][ik];
}
}
int main(int argc,char **argv)
{
int ii,ij,ik,max=0;
int v[POP_SIZE][GENE]; //本代群体基因库
int v_next[POP_SIZE][GENE]; //次代群体基因库
double eval[POP_SIZE]; //本代群体评估值
double eval_next[POP_SIZE]; //次代群体评估值
int best_cursor; //本代最优个体适值下标
int best_next_cursor; //次代最优个体适值下标
int worst_next_cursor; //次代最差个体适值下标
int best_gene[GENE]; //本代最优个体基因型
initialize(v);
for(ii=0;ii<NUM&&max<50;ii++)
{
evaluation(v,eval); //本代基因评估
best_cursor=best_eval(eval); //本代最优个体
cout<<endl<<"第"<<setw(3)<<ii+1<<"代最优基因:";
for(ij=0;ij<GENE;ij++) //保存本代最优基因
{
best_gene[ij]=v[best_cursor][ij];
cout<<best_gene[ij];
}
cout<<" 适值:"<<eval[best_cursor];
selection(eval,v,v_next); //选择
crossover(v_next); //交叉
mutation(v_next); //变异
evaluation(v_next,eval_next);
worst_next_cursor=worst_eval(eval_next);
for(ij=0;ij<GENE;ij++)
{
v_next[worst_next_cursor][ij]=best_gene[ij];
}
evaluation(v_next,eval_next);
best_next_cursor=best_eval(eval_next);
eval[best_cursor]==eval_next[best_next_cursor]?max++:max=0;
for(ij=0;ij<POP_SIZE;ij++)
{
for(ik=0;ik<GENE;ik++)
{
v[ij][ik]=v_next[ij][ik];
}
}
}
cout<<endl<<"最优基因适值为:"<<eval[best_cursor]<<endl;
cout<<"迭代次数为:"<<ii<<endl;
system("pause");
return 0;
}
/*
**本题最优值是38.818208
(1) 初始化群体;
(2) 计算群体上每个个体的适应度值;
(3) 按由个体适应度值所决定的某个规则选
择将进入下一代的个体;
(4) 按概率Pc进行交叉操作;
(5) 按概率Pm进行突变操作;
(6) 若没有满足某种停止条件,则转第(2)步,
否则进入下一步。
(7) 输出群体中适应度值最优的染色体作为问题的
满意解或最优解。
*/