简单易学的机器学习算法——Gibbs采样

一、Gibbs采样概述

前面介绍的Metropolis-Hastings采样为从指定分布中进行采样提供了一个统一的框架，但是采样的效率依赖于指定的分布的选择，若是选择的不好，会使得接受率比较低，大量的采样被拒绝，影响到整体的收敛速度。

Gibbs采样是Metropolis-Hastings采样算法的特殊形式，即找到一个已知的分布，使得接受率 α=1 。这样，每次的采样都会被接受，可以提高MCMC的收敛速度。

二、Gibbs采样算法的流程

在这部分，先直接给出Gibbs采样算法的流程，对于Gibbs采样算法的有效性将在第三部分给出论述，Gibbs采样算法的具体流程如下所述：

• 初始化时间 t=1
• 设置 u=(u1,u2,⋯,uN) 的值，并初始化初始状态 Θ(t)=u
• 重复以下的过程：
  
  • 令 t=t+1
  • 对每一维： i=1,2,⋯N
    
    • θ(t)1∼p(θ1∣θ(t−1)2,⋯,θ(t−1)N)
    • θ(t)2∼p(θ2∣θ(t)1,⋯,θ(t−1)N)
    • ⋯
    • θ(t)N−1∼p(θN−1∣θ(t)1,⋯,θ(t−1)N)
    • θ(t)N∼p(θN∣θ(t)1,⋯,θ(t)N−1)
• 直到 t=T

Gibbs采样有一个缺陷，必须知道条件分布。

三、上述过程满足细致平稳条件

为简单起见，我们假设所需采样的分布为一个二元分布 f(x,y) ，假设两个状态为 (x1,y1) 和 (x1,y2) 。已知：

p(x1,y1)⋅p(y2∣x1)=p(x1)⋅p(y1∣x1)⋅p(y2∣x1)

p(x1,y2)⋅p(y1∣x1)=p(x1)⋅p(y2∣x1)⋅p(y1∣x1)

所以有：

p(x1,y1)⋅p(y2∣x1)=p(x1,y2)⋅p(y1∣x1)

由此可见，Gibbs采样的过程是满足细致平稳条件的。这里直接取 p(y2∣x1) 为转移概率，则 α=1 ，可见Gibbs采样算法是Metropolis-Hastings采样的特殊形式。

四、实验

4.1、前提

假设从二项正态分布中进行采样，假设 Θ=(θ1,θ2) ，且：

Θ∼Norm(μ,Σ)

其中

μ=(μ1,μ2)

Σ=(1ρρ1)

已知：

θ1∼Norm(μ1+ρ(θ2−μ2),1−ρ2−−−−−√)

θ2∼Norm(μ2+ρ(θ1−μ1),1−ρ2−−−−−√)

4.2、流程

• 初始化时间 t=1
• 设置 u=(u1,u2) 的值，并初始化初始状态 Θ(t)=u
• 重复以下的过程：
  
  • 令 t=t+1
  • 对每一维： i=1,2
    
    • θ(t)1∼Norm(μ1+ρ(θ2−μ2),1−ρ2−−−−−√)
    • θ(t)2∼Norm(μ2+ρ(θ1−μ1),1−ρ2−−−−−√)
• 直到 t=T

4.3、实验代码

''' Date:20160704 @author: zhaozhiyong '''
import random
import math
import matplotlib.pyplot as plt

def p_ygivenx(x, m1, m2, s1, s2):
    return (random.normalvariate(m2 + rho * s2 / s1 * (x - m1), math.sqrt(1 - rho ** 2) * s2))

def p_xgiveny(y, m1, m2, s1, s2):
    return (random.normalvariate(m1 + rho * s1 / s2 * (y - m2), math.sqrt(1 - rho ** 2) * s1))

N = 5000
K = 20
x_res = []
y_res = []
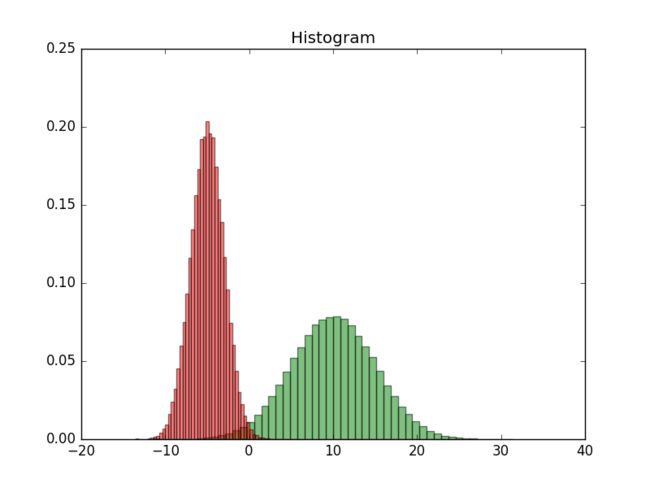
m1 = 10
m2 = -5
s1 = 5
s2 = 2

rho = 0.5
y = m2

for i in xrange(N):
    for j in xrange(K):
        x = p_xgiveny(y, m1, m2, s1, s2)
        y = p_ygivenx(x, m1, m2, s1, s2)
        x_res.append(x)
        y_res.append(y)

num_bins = 50
plt.hist(x_res, num_bins, normed=1, facecolor='green', alpha=0.5)
plt.hist(y_res, num_bins, normed=1, facecolor='red', alpha=0.5)
plt.title('Histogram')
plt.show()

4.4、实验结果