Trie树
翻译自topcoder中的一篇文章:https://www.topcoder.com/community/data-science/data-science-tutorials/using-tries/
简介
有很多种算法和数据结构可以用来在文本中建立字符串的索引和对字符串进行查找,一些已经被包含在了标准库中,一些还没有。Trie这种数据结构是一个还没有被包含在标准库中的一个很好的例子。
假设word表示单个字符串,dictionary表示一大堆字符串的集合。如果我们拥有一个dictionary,我们需要知道一个word是否存在dictionary中,那么trie这种数据结构可以帮助到我们。但是你可能会问题自己,“既然set< string>和hash table可以实现这个功能为什么要使用Trie?”。有两个主要的原因:
- Trie能够在O(L)的时间复杂度内实现插入和查询操作,L表示单个字符串的长度。这比set< string>快很多。
- set< string>和hash table只能在dictionary中查询和word完全匹配的字符串,但是Trie允许我们查询有一个字符不同的字符串,这个字符串拥有一个相同的前缀,但是最后的字符不同。
Trie在解决topcoder中的问题时是很有效的,同时在处理软件工程中的很多问题时也是很有效的。例如,考虑一个web浏览器,你知道web浏览器是怎么自动统计你的文本信息或者显示文本中字符串出现的次数的吗?是的,使用Trie你可以非常迅速的完成这个工作。你知道单词检查器是如何检查你输入的单词是否在词典中?同样Trie可以做到。你可以自己制定一个词典使用trie来检验单词的正确性而不是使用英语中的单词。
Trie tree是什么?
你可能了解过Trie tree是多么的棒,但是你可以还不是很清楚Trie是什么以及为什么它拥有Trie这个名字。Trie是”retrieval”(检索)这个单词的中缀这是因为Trie可以在一个dictionary中查询一个单词而仅仅使用这个单词的一部分前缀。Trie这种数据结构的主要思想如下:
- Trie是一棵树,这棵树的每一个节点代表一个单词或者一个前缀。
- 根节点表示一个空的字符串”“,根节点的直接子节点表示长度为1的前缀,和根节点相距两条边的节点表示长度为2的前缀,和根节点相距三条边的节点表示长度为3的前缀……,换句话说,如果一个节点和根节点相距k条边的长度,那么它代表长度为k的前缀。
- 假设v和w分别代表Trie中的两个节点,v是w的直接的父节点,那么v必定拥有w的前缀。
下面这幅图显示了一棵Trie树是如何表示“tree”, “trie”, “algo”, “assoc”, “all”和“also”这几个单词的:
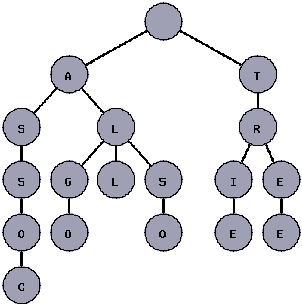
构造Trie树
Trie树可以通过多种方式实现,一些Trie树可能被用来在dictionary中查找一系列单词,这些单词和目标单词仅仅有一点不同;还有可能只查询和目标单词完全匹配的单词。下面的实现仅仅只包含了查询完全匹配的单词,计算拥有某个前缀的单词的数量。这些实现都是伪代码因为不同的程序员可以使用不同的代码来实现它。
我们只编写4个函数:
- addWord:这个函数添加单个word到dictionary中。
- countPreffixes:这个函数计算dictionary中有一个前缀prefix的单词的数量。
- countWords: 这个函数计算dictionary中完全匹配word的单词的数量。
- 我们的trie将只支持英文字母。
我们需要定义一个数据结构,这个数据结果包含Trie中每个节点的信息。由于我们需要知道完全匹配给定字符串的单词的数量,所以每个节点需要包含一个记录当前节点表示字符的字符的数量。注:词典dictionary中的单词可能会有重复。
由于我们需要知道有某个前缀的单词的数量,所以我们需要另外一个属性用来记录有多少个单词拥有某个节点表示的字符串作为前缀。同时,每一个节点都有指向它可能的26个子节点的指针。了解了这些细节,我们的数据结果可以如下定义:
structure Trie
integer words;
integer prefixes;
reference edges[26];我们需要定义下面这些函数:
initialize(vertex)
addWord(vertex, word);
integer countPrefixes(vertex, prefix);
integer countWords(vertex, word);首先定义初始化节点的函数
initialize(vertex)
vertex.words=0
vertex.prefixes=0
for i=0 to 26
edges[i]=NoEdgeaddWord函数
addWord函数包含两个参数,一个表示单词将要插入那个顶点,另一个表示将要插入的单词。当一个字符串word将要添加到节点vertex中时,我们可以根据word的第一个字符找到vertex中相关联的分支,如果这个分支不存在,那么我们需要创建它,并将word除去掉左边的单个字符后的单词插入到这个分支中。
addWord(vertex, word)
if isEmpty(word)
vertex.words=vertex.words+1
else
vertex.prefixes=vertex.prefixes+1
k=firstCharacter(word)
if(notExists(edges[k]))
edges[k]=createEdge()
initialize(edges[k])
cutLeftmostCharacter(word)
addWord(edges[k], word)countWords和countPrefixes
countWords和countPrefixes函数非常的相似。如果我们查找一个空的字符串我们只需要返回这个相关联的节点的words和prefixs属性即可。如果我们查找到一个非空的字符串,我们需要查看它的分支,如果这个分支不存在,返回0,如果这个分支存在,去除掉word最左边的字符后继续递归查找。
countWords(vertex, word)
k=firstCharacter(word)
if isEmpty(word)
return vertex.words
else if notExists(edges[k])
return 0
else
cutLeftmostCharacter(word)
return countWords(edges[k], word);
countPrefixes(vertex, prefix)
k=firstCharacter(prefix)
if isEmpty(word)
return vertex.prefixes
else if notExists(edges[k])
return 0
else
cutLeftmostCharacter(prefix)
return countWords(edges[k], prefix)分析
在介绍中你可能了解到Trie树的插入和查询的时间复杂度都是线性的,但是我们还没有进行分析。在插入和查询的过程中注意到在Trie Tree中每降低一层需要耗费常数的时间,同时每降低一层字符串的长度也减少了1.所以我们可以总结出每个函数降低L(L表示插入或删除字符串的长度)层就会终止。所以插入和查询的时间复杂度都是O(L)。内存的使用依赖于dictionary中的单词有多少前缀。
这是在leetCode中实现Trie树的代码。