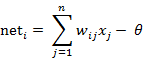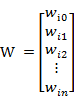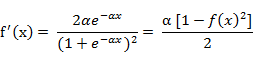BP神经网络学习及matlab实现
什么是神经网络?
神经网络是由很多神经元组成的,首先我们看一下,什么是神经元
上面这个图表示的就是一个神经元,我们不管其它书上说的那些什么树突,轴突的。我用个比较粗浅的解释,可能不太全面科学,但对初学者很容易理解:
1、我们把输入信号看成你在matlab中需要输入的数据,输进去神经网络后
2、这些数据的每一个都会被乘个数,即权值w,然后这些东东与阀值b相加后求和得到u,
3、上面只是线性变化,为了达到能处理非线性的目的,u做了个变换,变换的规则和传输函数有关
可能还有人问,那么那个阀值是什么呢?简单理解就是让这些数据做了个平移,这就是神经元工作的过程。处理后的结果又作为输入,可输给别的神经元,很多这样的神经元,就组成了网络。在matlab中具体用什么算法实现这些,我们先不管,我们需要注意的是怎么使用。比如使用BP的神经网络newff()构建一个网络,这些在后面的学习将提到。
BP网络的特点
①网络实质上实现了一个从输入到输出的映射功能,而数学理论已证明它具有实现任何复杂非线性映射的功能。这使得它特别适合于求解内部机制复杂的问题。我们无需建立模型,或了解其内部过程,只需输入,获得输出。只要BPNN结构优秀,一般20个输入函数以下的问题都能在50000次的学习以内收敛到最低误差附近。而且理论上,一个三层的神经网络,能够以任意精度逼近给定的函数,这是非常诱人的期望;
②网络能通过学习带正确答案的实例集自动提取“合理的”求解规则,即具有自学习能力;
③网络具有一定的推广、概括能力。
bp主要应用
回归预测(可以进行拟合,数据处理分析,事物预测,控制等)、 分类识别(进行类型划分,模式识别等),在后面的学习中,我都将给出实例程序。
但无论那种网络,什么方法,解决问题的精确度都无法打到100%的,但并不影响其使用,因为现实中很多复杂的问题,精确的解释是毫无意义的,有意义的解析必定会损失精度。
BP注意问题
1、BP算法的学习速度很慢,其原因主要有:
a 由于BP算法本质上为梯度下降法,而它所要优化的目标函数又非常复杂,因此,必然会出现“锯齿形现象”,这使得BP算法低效;
b 存在麻痹现象,由于优化的目标函数很复杂,它必然会在神经元输出接近0或1的情况下,出现一些平坦区,在这些区域内,权值误差改变很小,使训练过程几乎停顿;
c 为了使网络执行BP算法,不能用传统的一维搜索法求每次迭代的步长,而必须把步长的更新规则预先赋予网络,这种方法将引起算法低效。
2、网络训练失败的可能性较大,其原因有:
a 从数学角度看,BP算法为一种局部搜索的优化方法,但它要解决的问题为求解复杂非线性函数的全局极值,因此,算法很有可能陷入局部极值,使训练失败;
b 网络的逼近、推广能力同学习样本的典型性密切相关,而从问题中选取典型样本实例组成训练集是一个很困难的问题。
3、网络结构的选择:
尚无一种统一而完整的理论指导,一般只能由经验选定。为此,有人称神经网络的结构选择为一种艺术。而网络的结构直接影响网络的逼近能力及推广性质。因此,应用中如何选择合适的网络结构是一个重要的问题。
4、新加入的样本要影响已学习成功的网络,而且刻画每个输入样本的特征的数目也必须相同。
5、采用s型激活函数,由于输出层各神经元的理想输出值只能接近于1或0,而不能达到1或0,因此设置各训练样本的期望输出分量Tkp时,不能设置为1或0,设置0.9或0.1较为适宜。
什么是网络的泛化能力?
一个神经网路是否优良,与传统最小二乘之类的拟合评价不同(主要依据残差,拟合优度等),不是体现在其对已有的数据拟合能力上,而是对后来的预测能力,既泛化能力。
网络的预测能力(也称泛化能力、推广能力)与训练能力(也称逼近能力、学习能力)的矛盾。一般情况下,训练能力差时,预测能力也差,并且一定程度上,随训练能力地提高,预测能力也提高。但这种趋势有一个极限,当达到此极限时,随训练能力的提高,预测能力反而下降,即出现所谓“过拟合”现象。此时,网络学习了过多的样本细节,而不能反映样本内含的规律。
过拟合是什么,怎么处理?
神经网络计算不能一味地追求训练误差最小,这样很容易出现“过拟合”现象,只要能够实时检测误差率的变化就可以确定最佳的训练次数,比如15000次左右的学习次数,如果你不观察,设成500000次学习,不仅需要很长时间来跑,而且最后结果肯定令人大失所望。
避免过拟合的一种方法是:在数据输入中,给训练的数据分类,分为正常训练用、变量数据、测试数据,在后面节将讲到如何进行这种分类。
其中变量数据,在网络训练中,起到的作用就是防止过拟合状态。
学习速率有什么作用?
学习速率这个参数可以控制能量函数的步幅,并且如果设为自动调整的话,可以在误差率经过快速下降后,将学习速率变慢,从而增加BPNN的稳定性。
此时训练方法采用
- net.trainFcn = 'traingda'; % 变学习率梯度下降算法
- net.trainFcn = 'traingdx'; % 变学习率动量梯度下降算法
- 可以定义一个变动的学习速率,如
- p = [-1 -1 2 2; 0 5 0 5];
- t = [-1 -1 1 1];
- net = newff(p,t,3,{},'traingda');
- net.trainParam.lr = 0.05;
- net.trainParam.lr_inc = 1.05;
- net = train(net,p,t);
- y = sim(net,p)
在后面的拟合例题中,我们也将用到学习速率这个参数。
神经网络的权值和阈值分别是个什么概念?
第一节中,我们已经谈到了权值和阀值的概念。这里我们更深入的说明一下,因为他们很重要,关系到网络最后的结果。权值和阈值是神经元之间的连接,将数据输入计算出一个输出,然后与实际输出比较,误差反传,不断调整权值和阈值。
假如下面两个点属于不同的类,须设计分类器将他们分开
p1=[1 1 -1]';
p2=[1 -1 -1]';
这里用单层神经元感知器,假设初始权值
w=[0.2 0.2 0.3]
同时假设初始阀值
b=-0.3
输出 a1 a2
a1=hardlims(w*p1+b)
a2=hardlims(w*p2+b)
如果不能分开,还须不断调整w,b
用BP逼近非线性函数,如何提高训练精度
(1)调整网络结构
增加网络的层数可以进一步降低误差,提高精度但会使网络复杂化,从而增加网络的训练时间。精度的提高实际上也可以通过增加隐层神经元的数目来获得,其效果更容易观察和掌握,所以应优先考虑。
(2)初始值选取
为了使误差尽可能小 ,需要合理选择初始权重和偏置,如果太大就容易陷入饱和区,导致停顿 。一般应选为均匀分布的小数,介于 (-1,1) 。
(3)学习速率调整
学习速率的选取很重要 ,大了可能导致系统不稳定,小了会导致训练周期过长、收敛慢,达不到要求的误差。一般倾向于选取较小的学习速率以保持系统稳定,通过观察误差下降曲线来判断。下降较快说明学习率比较合适,若有较大振荡则说明学习率偏大。同时,由于网络规模大小的不同,学习率选择应当针对其进行调整。采用变学习速率的方案,令学习速率随学习进展而逐步减少,可收到良好的效果。
(4)期望误差
期望误差当然希望越小越好,但是也要有合适值。
为了充分利用数据,得到最优的网络训练结果,在网络建立前应该进行的基本数据处理问题,包括:
(1)BP神经网络matlab实现的基本步骤
(2)数据归一化问题和方法
(3)输入训练数据的乱序排法,以及分类方法
(4)如何查看和保存训练的结果
(5)每次结果不一样问题。
用matlab实现bp,其实很简单,按下面步骤基本可以了
BP神经网络matlab实现的基本步骤
1、数据归一化
2、数据分类,主要包括打乱数据顺序,抽取正常训练用数据、变量数据、测试数据
3、建立神经网络,包括设置多少层网络(一般3层以内既可以,每层的节点数(具体节点数,尚无科学的模型和公式方法确定,可采用试凑法,但输出层的节点数应和需要输出的量个数相等),设置隐含层的传输函数等。关于网络具体建立使用方法,在后几节的例子中将会说到。
4、指定训练参数进行训练,这步非常重要,在例子中,将详细进行说明
5、完成训练后,就可以调用训练结果,输入测试数据,进行测试
6、数据进行反归一化
7、误差分析、结果预测或分类,作图等
数据归一化问题
归一化的意义:
首先说一下,在工程应用领域中,应用BP网络的好坏最关键的仍然是输入特征选择和训练样本集的准备,若样本集代表性差、矛盾样本多、数据归一化存在问题,那么,使用多复杂的综合算法、多精致的网络结构,建立起来的模型预测效果不会多好。若想取得实际有价值的应用效果,从最基础的数据整理工作做起吧,会少走弯路的。
归一化是为了加快训练网络的收敛性,具体做法是:
1 把数变为(0,1)之间的小数
主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速,应该归到数字信号处理范畴之内。
2 把有量纲表达式变为无量纲表达式
归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量
比如,复数阻抗可以归一化书写:Z = R + jωL = R(1 + jωL/R) ,复数部分变成了纯数量了,没有量纲。另外,微波之中也就是电路分析、信号系统、电磁波传输等,有很多运算都可以如此处理,既保证了运算的便捷,又能凸现出物理量的本质含义。
神经网络归一化方法:
由于采集的各数据单位不一致,因而须对数据进行[-1,1]归一化处理,归一化方法主要有如下几种,供大家参考:
1、线性函数转换,表达式如下:
y=(x-MinValue)/(MaxValue-MinValue)
说明:x、y分别为转换前、后的值,MaxValue、MinValue分别为样本的最大值和最小值。
2、对数函数转换,表达式如下:
y=log10(x)
说明:以10为底的对数函数转换。
3、反余切函数转换,表达式如下:
y=atan(x)*2/PI
matlab中归一化的实现:
matlab中的归一化处理有五种方法,只会其中一种就可以了,我喜欢用第4种,因为习惯和方便
注意:第一组和第二组归一化函数在Matlab7.0以上已遗弃,他们的用法相似,pre**是归一化,post**是反归一化,tram**是使用同样的设置归一化另外一组数据
1. 内部函数premnmx、postmnmx、tramnmx,将数据归一化到(-1,1)
premnmx的语法格式是
:[Pn,minp,maxp,Tn,mint,maxt]=premnmx(P,T)
其中P,T分别为原始输入和输出数据,minp和maxp分别为P中的最小值和最大值。mint和maxt分别为T的最小值和最大值。
我们在训练网络时,如果所用的是经过归一化的样本数据,那么以后使用网络时所用的新数据也应该和样本数据接受相同的预处理,这就要用到tramnmx,换句话说使用同一个归一化设置(setting)归一化另外一组数据。如下所示:
[Pn]=tramnmx(P,minp,maxp)
其中P和Pn分别为变换前、后的输入数据,maxp和minp分别为premnmx函返回的最大值maxp和最小值minp。
2、prestd、poststd、trastd归化数据到(0,1)
用法与1差不多。详细可以help prestd。
上述两种方法是可以相互转化的,比如,第一种归化后的数据为p,则(1+p)./2的结果就是第二种了
3、mapminmax()将数据归一化到(-1,1),是6.5中**mnmx系列的替换函数
该函数同时可以执行归一化、反归一化和归一化其他数据的功能,具体看帮助和后面的实例
- % 归一化数据输入为p,输出为t
- [normInput,ps] = mapminmax(p);
- [normTarget,ts] = mapminmax(t);
- % 反归一化
- trainOutput = mapminmax('reverse',normTrainOutput,ts);
- trainInsect = mapminmax('reverse',trainSamples.T,ts);
- validateOutput = mapminmax('reverse',normValidateOutput,ts);
- validateInsect = mapminmax('reverse',validateSamples.T,ts);
- testOutput = mapminmax('reverse',normTestOutput,ts);
- testInsect = mapminmax('reverse',testSamples.T,ts);
- %例子:
- x1 = [1 2 4; 1 1 1; 3 2 2; 0 0 0]
- [y1,PS] = mapminmax(x1,0,1)% 归化到 [0,1],若不填,则默认为[-1,1]
- %还原:
- x1_again = mapminmax('reverse',y1,PS)
4、mapstd()将数据归一化到(0,1),是6.5中**std系列的替代函数
同理,3和4两种方法是可以相互转化的,比如,第一种归化后的数据为p,则(1+p)./2的结果就是第二种了。
5、自己写归一化函数,这个网上很多,大家可以百度下
输入训练数据的乱序排法,以及分类
注意:dividevec()函数在7.6版本还可以使用
把数据重新打乱顺序,进行输入,可以让数据更加具备典型性和更优良的泛化能力!
把数据进行打乱,并分类为:训练输入数据、变量数据、测试数据的方法
我用百度搜了一下,发现有些方法,但居然很少看到使用matlab内部函数直接进行的,其实matlab自带的内部函数dividevec,完全能胜任上述工作,推荐!
但这个存在一个问题是,因为打乱了,最后分析结果的时候,数据重新排列困难,因为丢失了数据在数组中的位置参数。具体用法可以参见下面我的bp交通预测的例子。
因为我用的7.0版本,Neural Network Toolbox Version 5.0.2 (R2007a)
昨天,我去mathworks公司查看了一下nnet的新手册,上述问题得到了解决,里面视乎没有介绍dividverc这个函数了,但增加了新的函数来完成上述功能,并返回标号(手头没装新版本Neural Network Toolbox Version 6.0 (R2008a)),看guide大概是这个意思(有新版本的,可以试一下,这个函数是不是这个意思):
divideblock,divideind,divideint和dividerand
上述函数,用法和功能基本相同,只是打乱的方法不一样,分别是block方法抽取、按数组标号自定义抽取、交错索引抽取和随机抽。
下面以divideblock为例,讲解其基本用法:
[trainV,valV,testV,trainInd,valInd,testInd] =divideblock(allV,trainRatio,valRatio,testRatio)
[训练数据,变量数据,测试数据,训练数据矩阵的标号,变量数据标号,测试数据标号] =divideblock(所有数据,训练数据百分比,变量数据百分比,测试数据百分比)
其实dividevec和后面四个分类函数的区别在于,dividevec一般直接在Matlab代码中调用。
而后面四个函数是通过设置网络的divideFcn函数来实现,比如,net.divideFcn='divideblock',但不是说不可以在代码中像dividevec直接调用
如何查看和保存结果
训练好的权值、阈值的输出方法是:
输入到隐层权值:
w1=net.iw{1,1}
隐层阈值:
theta1=net.b{1}
隐层到输出层权值:
w2=net.lw{2,1};
输出层阈值:
theta2=net.b{2}
训练好的BP神经网络保存:
%保存
save file_name net_name%Matlab自动将网络保存为mat数据文件,下次使用时可以直接载入
%载入
load file_name
每次结果不一样问题
因为每次初始化网络时都是随机的,而且训练终止时的误差也不完全相同,结果训练后的权植和阀也不完全相同(大致是一样的),所以每次训练后的结果也略有不同。
找到比较好的结果后,用命令save filen_ame net_name保存网络,可使预测的结果不会变化,在需要的调用时用命令load filename载入。
关于如何找到比较好的结果,进行保存,可以设置误差,在循环中保存,具体使用可以参看bp交通预测优化后的例子
- %bp神经网络进行交通预测的Matlab源代码
- % BP 神经网络用于预测
- % 使用平台 - Matlab7.0
- % 数据为1986年到2000年的交通量 ,网络为3输入,1输出
- % 15组数据,其中9组为正常训练数据,3组为变量数据,3组为测试数据
- %by akjuan
- %all rights preserved by www.4math.cn
- %2008.11
- clc
- clear
- %---------------------------------------------------
- %原始数据
- %---------------------------------------------------
- year=1986:2000;%数据是从1986到2000年的
- p=[493 372 445;372 445 176;445 176 235;176 235 378;235 378 429;...
- 378 429 561;429 561 651;561 651 467;651 467 527;467 527 668;...
- 527 668 841; 668 841 526;841 526 480;526 480 567;480 567 685]';%输入数据,共15组,每组3个输入
- t=[176 235 378 429 561 651 467 527 668 841 526 480 567 685 507];%输出数据,共15组,每组1个输出
- %---------------------------------------------------
- %数据归一化处理
- %mapminmax函数默认将数据归一化到[-1,1],调用形式如下
- %[y,ps] =%mapminmax(x,ymin,ymax)
- %x需归化的数据输入
- %ymin,ymax为需归化到的范围,不填默认为归化到[-1,1]
- %y归一化后的样本数据
- %ps处理设置,ps主要在结果反归一化中需要调用,或者使用同样的settings归一化另外一组数据
- %---------------------------------------------------
- [normInput,ps] = mapminmax(p);
- [normTarget,ts] = mapminmax(t);
- %---------------------------------------------------
- %数据乱序,及分类处理
- %将输入的15组数据的20%,即3组,用来作为测试数据;
- % 样本的20%,即3组,用来作为变化数据;
- %另外9组用来正常输入,用来训练;
- %dividevec()用来重新随机抽取上述三种分类的数据,原来的顺序被打乱
- %函数调用的语法
- %[trainV,valV,testV] = dividevec(p,t,valPercent,testPercent)
- %输入p为输入数据,t为输出数据
- %valPercent为训练用的变化数据在总输入中的百分比
- %testPercent为训练用的测试数据在总输入中的百分比
- %输出trainV,valV,testV分别为按乱序及相应百分比,抽取得到的数据
- %另外,打乱后的数据,p和t都是对应的,请放心使用
- %---------------------------------------------------
- testPercent = 0.20; % Adjust as desired
- validatePercent = 0.20; % Adust as desired
- [trainSamples,validateSamples,testSamples] = dividevec(normInput,normTarget,validatePercent,testPercent);
- %---------------------------------------------------
- % 设置网络参数
- %---------------------------------------------------
- NodeNum1 = 20; % 隐层第一层节点数
- NodeNum2 = 40; % 隐层第二层节点数
- TypeNum = 1; % 输出维数
- TF1 = 'tansig';TF2 = 'tansig'; TF3 = 'tansig';%各层传输函数,TF3为输出层传输函数
- %如果训练结果不理想,可以尝试更改传输函数,以下这些是各类传输函数
- %TF1 = 'tansig';TF2 = 'logsig';
- %TF1 = 'logsig';TF2 = 'purelin';
- %TF1 = 'tansig';TF2 = 'tansig';
- %TF1 = 'logsig';TF2 = 'logsig';
- %TF1 = 'purelin';TF2 = 'purelin';
- %注意创建BP网络函数newff()的参数调用,在新版本(7.6)中已改变
- net=newff(minmax(normInput),[NodeNum1,NodeNum2,TypeNum],{TF1 TF2 TF3},'traingdx');%创建四层BP网络
- %---------------------------------------------------
- % 设置训练参数
- %---------------------------------------------------
- net.trainParam.epochs=10000;%训练次数设置
- net.trainParam.goal=1e-6;%训练目标设置
- net.trainParam.lr=0.01;%学习率设置,应设置为较少值,太大虽然会在开始加快收敛速度,但临近最佳点时,会产生动荡,而致使无法收敛
- %---------------------------------------------------
- % 指定训练函数
- %---------------------------------------------------
- % net.trainFcn = 'traingd'; % 梯度下降算法
- % net.trainFcn = 'traingdm'; % 动量梯度下降算法
- %
- % net.trainFcn = 'traingda'; % 变学习率梯度下降算法
- % net.trainFcn = 'traingdx'; % 变学习率动量梯度下降算法
- %
- % (大型网络的首选算法)
- % net.trainFcn = 'trainrp'; % RPROP(弹性BP)算法,内存需求最小
- %
- % (共轭梯度算法)
- % net.trainFcn = 'traincgf'; % Fletcher-Reeves修正算法
- % net.trainFcn = 'traincgp'; % Polak-Ribiere修正算法,内存需求比Fletcher-Reeves修正算法略大
- % net.trainFcn = 'traincgb'; % Powell-Beal复位算法,内存需求比Polak-Ribiere修正算法略大
- %
- % (大型网络的首选算法)
- %net.trainFcn = 'trainscg'; % Scaled Conjugate Gradient算法,内存需求与Fletcher-Reeves修正算法相同,计算量比上面三种算法都小很多
- % net.trainFcn = 'trainbfg'; % Quasi-Newton Algorithms - BFGS Algorithm,计算量和内存需求均比共轭梯度算法大,但收敛比较快
- % net.trainFcn = 'trainoss'; % One Step Secant Algorithm,计算量和内存需求均比BFGS算法小,比共轭梯度算法略大
- %
- % (中型网络的首选算法)
- %net.trainFcn = 'trainlm'; % Levenberg-Marquardt算法,内存需求最大,收敛速度最快
- % net.trainFcn = 'trainbr'; % 贝叶斯正则化算法
- %
- % 有代表性的五种算法为:'traingdx','trainrp','trainscg','trainoss', 'trainlm'
- net.trainfcn='traingdm';
- [net,tr] = train(net,trainSamples.P,trainSamples.T,[],[],validateSamples,testSamples);
- %---------------------------------------------------
- % 训练完成后,就可以调用sim()函数,进行仿真了
- %---------------------------------------------------
- [normTrainOutput,Pf,Af,E,trainPerf] = sim(net,trainSamples.P,[],[],trainSamples.T);%正常输入的9组p数据,BP得到的结果t
- [normValidateOutput,Pf,Af,E,validatePerf] = sim(net,validateSamples.P,[],[],validateSamples.T);%用作变量3的数据p,BP得到的结果t
- [normTestOutput,Pf,Af,E,testPerf] = sim(net,testSamples.P,[],[],testSamples.T);%用作测试的3组数据p,BP得到的结果t
- %---------------------------------------------------
- % 仿真后结果数据反归一化,如果需要预测,只需将预测的数据P填入
- % 将获得预测结果t
- %---------------------------------------------------
- trainOutput = mapminmax('reverse',normTrainOutput,ts);%正常输入的9组p数据,BP得到的归一化后的结果t
- trainInsect = mapminmax('reverse',trainSamples.T,ts);%正常输入的9组数据t
- validateOutput = mapminmax('reverse',normValidateOutput,ts);%用作变量3的数据p,BP得到的归一化的结果t
- validateInsect = mapminmax('reverse',validateSamples.T,ts);%用作变量3的数据t
- testOutput = mapminmax('reverse',normTestOutput,ts);%用作变量3组数据p,BP得到的归一化的结果t
- testInsect = mapminmax('reverse',testSamples.T,ts);%用作变量3组数据t
- %---------------------------------------------------
- % 数据分析和绘图
- %---------------------------------------------------
- figure
- plot(1:12,[trainOutput validateOutput],'b-',1:12,[trainInsect validateInsect],'g--',13:15,testOutput,'m*',13:15,testInsect,'ro');
- title('o为真实值,*为预测值')
- xlabel('年份');
- ylabel('交通量(辆次/昼夜)');
但通过程序运行后,可以看出,预测效果并不理想,如何得到理想的预测训练结果,下面是基本思路及matlab的实现:
1、设置一个误差项,为测试数据的网络仿真结果和实际结果偏差,并设置一个自己能接受的精度值
2、每次训练网络后,将这个误差和设置值比较,也可通过测试获得网络能给出的最高预测精度
3、得到满意训练网络后,保存BP结果,以便下次调用
下面这个程序是在第四节程序基础上优化而来,可以运行前面的程序和这个程序,比较两者的差别,可以通过修改eps来控制预测的误差!
- %bp神经网络进行交通预测的Matlab源代码
- % BP 神经网络用于预测
- % 使用平台 - Matlab7.0
- % 数据为1986年到2000年的交通量 ,网络为3输入,1输出
- % 15组数据,其中9组为正常训练数据,3组为变量数据,3组为测试数据
- %by akjuan
- %all rights preserved by www.matlabsky.cn
- %2008.11
- clc
- clear
- All_error=[];%所有误差存储
- %---------------------------------------------------
- %原始数据
- %---------------------------------------------------
- year=1986:2000;%数据是从1986到2000年的
- p=[493 372 445;372 445 176;445 176 235;176 235 378;235 378 429;...
- 378 429 561;429 561 651;561 651 467;651 467 527;467 527 668;...
- 527 668 841; 668 841 526;841 526 480;526 480 567;480 567 685]';%输入数据,共15组,每组3个输入
- t=[176 235 378 429 561 651 467 527 668 841 526 480 567 685 507];%输出数据,共15组,每组1个输出
- %---------------------------------------------------
- %数据归一化处理
- %mapminmax函数默认将数据归一化到[-1,1],调用形式如下
- %[y,ps] =%mapminmax(x,ymin,ymax)
- %x需归化的数据输入
- %ymin,ymax为需归化到的范围,不填默认为归化到[-1,1]
- %y归一化后的样本数据
- %ps处理设置,ps主要在结果反归一化中需要调用,或者使用同样的settings归一化另外一组数据
- %---------------------------------------------------
- [normInput,ps] = mapminmax(p);
- [normTarget,ts] = mapminmax(t);
- %---------------------------------------------------
- %数据乱序,及分类处理
- %将输入的15组数据的20%,即3组,用来作为测试数据;
- % 样本的20%,即3组,用来作为变化数据;
- %另外9组用来正常输入,用来训练;
- %dividevec()用来重新随机抽取上述三种分类的数据,原来的顺序被打乱
- %函数调用的语法
- %[trainV,valV,testV] = dividevec(p,t,valPercent,testPercent)
- %输入p为输入数据,t为输出数据
- %valPercent为训练用的变化数据在总输入中的百分比
- %testPercent为训练用的测试数据在总输入中的百分比
- %输出trainV,valV,testV分别为按乱序及相应百分比,抽取得到的数据
- %另外,打乱后的数据,p和t都是对应的,请放心使用
- %---------------------------------------------------
- testPercent = 0.20; % Adjust as desired
- validatePercent = 0.20; % Adust as desired
- [trainSamples,validateSamples,testSamples] = dividevec(normInput,normTarget,validatePercent,testPercent);
- for j=1:200
- %---------------------------------------------------
- % 设置网络参数
- %---------------------------------------------------
- NodeNum1 = 20; % 隐层第一层节点数
- NodeNum2=40; % 隐层第二层节点数
- TypeNum = 1; % 输出维数
- TF1 = 'tansig';TF2 = 'tansig'; TF3 = 'tansig';%各层传输函数,TF3为输出层传输函数
- %如果训练结果不理想,可以尝试更改传输函数,以下这些是各类传输函数
- %TF1 = 'tansig';TF2 = 'logsig';
- %TF1 = 'logsig';TF2 = 'purelin';
- %TF1 = 'tansig';TF2 = 'tansig';
- %TF1 = 'logsig';TF2 = 'logsig';
- %TF1 = 'purelin';TF2 = 'purelin';
- net=newff(minmax(normInput),[NodeNum1,NodeNum2,TypeNum],{TF1 TF2 TF3},'traingdx');%网络创建
- %---------------------------------------------------
- % 设置训练参数
- %---------------------------------------------------
- net.trainParam.epochs=10000;%训练次数设置
- net.trainParam.goal=1e-6;%训练目标设置
- net.trainParam.lr=0.01;%学习率设置,应设置为较少值,太大虽然会在开始加快收敛速度,但临近最佳点时,会产生动荡,而致使无法收敛
- %---------------------------------------------------
- % 指定训练参数
- %---------------------------------------------------
- % net.trainFcn = 'traingd'; % 梯度下降算法
- % net.trainFcn = 'traingdm'; % 动量梯度下降算法
- %
- % net.trainFcn = 'traingda'; % 变学习率梯度下降算法
- % net.trainFcn = 'traingdx'; % 变学习率动量梯度下降算法
- %
- % (大型网络的首选算法)
- % net.trainFcn = 'trainrp'; % RPROP(弹性BP)算法,内存需求最小
- %
- % (共轭梯度算法)
- % net.trainFcn = 'traincgf'; % Fletcher-Reeves修正算法
- % net.trainFcn = 'traincgp'; % Polak-Ribiere修正算法,内存需求比Fletcher-Reeves修正算法略大
- % net.trainFcn = 'traincgb'; % Powell-Beal复位算法,内存需求比Polak-Ribiere修正算法略大
- %
- % (大型网络的首选算法)
- %net.trainFcn = 'trainscg'; % Scaled Conjugate Gradient算法,内存需求与Fletcher-Reeves修正算法相同,计算量比上面三种算法都小很多
- % net.trainFcn = 'trainbfg'; % Quasi-Newton Algorithms - BFGS Algorithm,计算量和内存需求均比共轭梯度算法大,但收敛比较快
- % net.trainFcn = 'trainoss'; % One Step Secant Algorithm,计算量和内存需求均比BFGS算法小,比共轭梯度算法略大
- %
- % (中型网络的首选算法)
- %net.trainFcn = 'trainlm'; % Levenberg-Marquardt算法,内存需求最大,收敛速度最快
- % net.trainFcn = 'trainbr'; % 贝叶斯正则化算法
- %
- % 有代表性的五种算法为:'traingdx','trainrp','trainscg','trainoss', 'trainlm'
- net.trainfcn='traingdm';
- [net,tr] = train(net,trainSamples.P,trainSamples.T,[],[],validateSamples,testSamples);
- %---------------------------------------------------
- % 训练完成后,就可以调用sim()函数,进行仿真了
- %---------------------------------------------------
- [normTrainOutput,Pf,Af,E,trainPerf] = sim(net,trainSamples.P,[],[],trainSamples.T);%正常输入的9组p数据,BP得到的结果t
- [normValidateOutput,Pf,Af,E,validatePerf] = sim(net,validateSamples.P,[],[],validateSamples.T);%用作变量3的数据p,BP得到的结果t
- [normTestOutput,Pf,Af,E,testPerf] = sim(net,testSamples.P,[],[],testSamples.T);%用作测试的3组数据p,BP得到的结果t
- %---------------------------------------------------
- % 仿真后结果数据反归一化,如果需要预测,只需将预测的数据P填入
- % 将获得预测结果t
- %---------------------------------------------------
- trainOutput = mapminmax('reverse',normTrainOutput,ts);%正常输入的9组p数据,BP得到的归一化后的结果t
- trainInsect = mapminmax('reverse',trainSamples.T,ts);%正常输入的9组数据t
- validateOutput = mapminmax('reverse',normValidateOutput,ts);%用作变量3的数据p,BP得到的归一化的结果t
- validateInsect = mapminmax('reverse',validateSamples.T,ts);%用作变量3的数据t
- testOutput = mapminmax('reverse',normTestOutput,ts);%用作变量3组数据p,BP得到的归一化的结果t
- testInsect = mapminmax('reverse',testSamples.T,ts);%用作变量3组数据t
- %绝对误差计算
- absTrainError = trainOutput-trainInsect;
- absTestError = testOutput-testInsect;
- error_sum=sqrt(absTestError(1).^2+absTestError(2).^2+absTestError(3).^2);
- All_error=[All_error error_sum];
- eps=90;%其为3组测试数据的标准差,或者每个数据偏差在一定范围内而判别
- if ((abs(absTestError(1))<=30 )&(abs(absTestError(2))<=30)&(abs(absTestError(3))<=30)|(error_sum<=eps))
- save mynetdata net
- break
- end
- j
- end
- j
- Min_error_sqrt=min(All_error)
- testOutput
- testInsect
- %---------------------------------------------------
- % 数据分析和绘图
- %---------------------------------------------------
- figure
- plot(1:12,[trainOutput validateOutput],'b-',1:12,[trainInsect validateInsect],'g--',13:15,testOutput,'m*',13:15,testInsect,'ro');
- title('o为真实值,*为预测值')
- xlabel('年份');
- ylabel('交通量(辆次/昼夜)');
- figure
- xx=1:length(All_error);
- plot(xx,All_error)
- title('误差变化图')
本文主要内容包括: (1) 介绍神经网络基本原理,(2) AForge.NET实现前向神经网络的方法,(3) Matlab实现前向神经网络的方法 。
第0节、引例
本文以Fisher的Iris数据集作为神经网络程序的测试数据集。Iris数据集可以在http://en.wikipedia.org/wiki/Iris_flower_data_set 找到。这里简要介绍一下Iris数据集:
有一批Iris花,已知这批Iris花可分为3个品种,现需要对其进行分类。不同品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度会有差异。我们现有一批已知品种的Iris花的花萼长度、花萼宽度、花瓣长度、花瓣宽度的数据。
一种解决方法是用已有的数据训练一个神经网络用作分类器。
如果你只想用C#或Matlab快速实现神经网络来解决你手头上的问题,或者已经了解神经网络基本原理,请直接跳到第二节——神经网络实现。
第一节、神经网络基本原理
1. 人工神经元( Artificial Neuron )模型
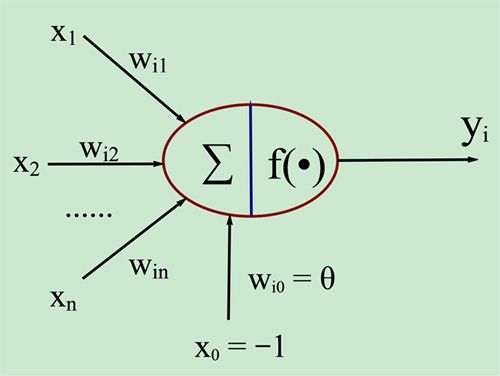
人工神经元是神经网络的基本元素,其原理可以用下图表示:
图1. 人工神经元模型
图中x1~xn是从其他神经元传来的输入信号,wij表示表示从神经元j到神经元i的连接权值,θ表示一个阈值 ( threshold ),或称为偏置( bias )。则神经元i的输出与输入的关系表示为:
![]()
图中 yi表示神经元i的输出,函数f称为激活函数 ( Activation Function )或转移函数 ( Transfer Function ) ,net称为净激活(net activation)。若将阈值看成是神经元i的一个输入x0的权重wi0,则上面的式子可以简化为:
![]()
若用X表示输入向量,用W表示权重向量,即:
X = [ x0 , x1 , x2 , ....... , xn ]
则神经元的输出可以表示为向量相乘的形式:
![]()
![]()
若神经元的净激活net为正,称该神经元处于激活状态或兴奋状态(fire),若净激活net为负,则称神经元处于抑制状态。
图1中的这种“阈值加权和”的神经元模型称为M-P模型 ( McCulloch-Pitts Model ),也称为神经网络的一个处理单元( PE, Processing Element )。
2. 常用激活函数
激活函数的选择是构建神经网络过程中的重要环节,下面简要介绍常用的激活函数。
(1) 线性函数 ( Liner Function )
![]()
(2) 斜面函数 ( Ramp Function )
(3) 阈值函数 ( Threshold Function )
以上3个激活函数都属于线性函数,下面介绍两个常用的非线性激活函数。
(4) S形函数 ( Sigmoid Function )
该函数的导函数:
(5) 双极S形函数
该函数的导函数:
S形函数与双极S形函数的图像如下:
图3. S形函数与双极S形函数图像
双极S形函数与S形函数主要区别在于函数的值域,双极S形函数值域是(-1,1),而S形函数值域是(0,1)。
由于S形函数与双极S形函数都是可导的(导函数是连续函数),因此适合用在BP神经网络中。(BP算法要求激活函数可导)
3. 神经网络模型
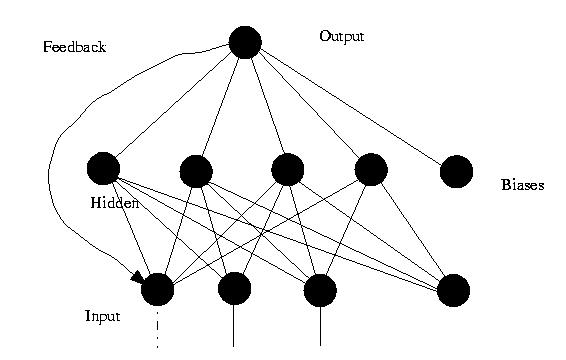
神经网络是由大量的神经元互联而构成的网络。根据网络中神经元的互联方式,常见网络结构主要可以分为下面3类:
(1) 前馈神经网络 ( Feedforward Neural Networks )
前馈网络也称前向网络。这种网络只在训练过程会有反馈信号,而在分类过程中数据只能向前传送,直到到达输出层,层间没有向后的反馈信号,因此被称为前馈网络。感知机( perceptron)与BP神经网络就属于前馈网络。
图4 中是一个3层的前馈神经网络,其中第一层是输入单元,第二层称为隐含层,第三层称为输出层(输入单元不是神经元,因此图中有2层神经元)。
图4. 前馈神经网络
对于一个3层的前馈神经网络N,若用X表示网络的输入向量,W1~W3表示网络各层的连接权向量,F1~F3表示神经网络3层的激活函数。
那么神经网络的第一层神经元的输出为:
O1 = F1( XW1 )
第二层的输出为:
O2 = F2 ( F1( XW1 ) W2 )
输出层的输出为:
O3 = F3( F2 ( F1( XW1 ) W2 ) W3 )
若激活函数F1~F3都选用线性函数,那么神经网络的输出O3将是输入X的线性函数。因此,若要做高次函数的逼近就应该选用适当的非线性函数作为激活函数。
(2) 反馈神经网络 ( Feedback Neural Networks )
反馈型神经网络是一种从输出到输入具有反馈连接的神经网络,其结构比前馈网络要复杂得多。典型的反馈型神经网络有:Elman网络和Hopfield网络。
图5. 反馈神经网络
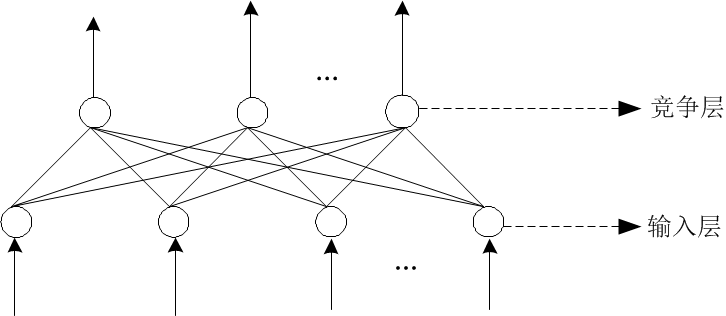
(3) 自组织网络 ( SOM ,Self-Organizing Neural Networks )
自组织神经网络是一种无导师学习网络。它通过自动寻找样本中的内在规律和本质属性,自组织、自适应地改变网络参数与结构。
图6. 自组织网络
4. 神经网络工作方式
神经网络运作过程分为学习和工作两种状态。
(1)神经网络的学习状态
网络的学习主要是指使用学习算法来调整神经元间的联接权,使得网络输出更符合实际。学习算法分为有导师学习( Supervised Learning )与无导师学习( Unsupervised Learning )两类。
有导师学习算法将一组训练集 ( training set )送入网络,根据网络的实际输出与期望输出间的差别来调整连接权。有导师学习算法的主要步骤包括:
1) 从样本集合中取一个样本(Ai,Bi);
2) 计算网络的实际输出O;
3) 求D=Bi-O;
4) 根据D调整权矩阵W;
5) 对每个样本重复上述过程,直到对整个样本集来说,误差不超过规定范围。
BP算法就是一种出色的有导师学习算法。
无导师学习抽取样本集合中蕴含的统计特性,并以神经元之间的联接权的形式存于网络中。
Hebb学习律是一种经典的无导师学习算法。
(2) 神经网络的工作状态
神经元间的连接权不变,神经网络作为分类器、预测器等使用。
下面简要介绍一下Hebb学习率与Delta学习规则 。
(3) 无导师学习算法:Hebb学习率
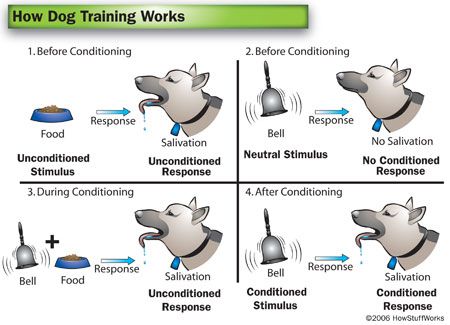
Hebb算法核心思想是,当两个神经元同时处于激发状态时两者间的连接权会被加强,否则被减弱。
为了理解Hebb算法,有必要简单介绍一下条件反射实验。巴甫洛夫的条件反射实验:每次给狗喂食前都先响铃,时间一长,狗就会将铃声和食物联系起来。以后如果响铃但是不给食物,狗也会流口水。
图7. 巴甫洛夫的条件反射实验
受该实验的启发,Hebb的理论认为在同一时间被激发的神经元间的联系会被强化。比如,铃声响时一个神经元被激发,在同一时间食物的出现会激发附近的另一个神经元,那么这两个神经元间的联系就会强化,从而记住这两个事物之间存在着联系。相反,如果两个神经元总是不能同步激发,那么它们间的联系将会越来越弱。
Hebb学习律可表示为:
![]()
其中wij表示神经元j到神经元i的连接权,yi与yj为两个神经元的输出,a是表示学习速度的常数。若yi与yj同时被激活,即yi与yj同时为正,那么Wij将增大。若yi被激活,而yj处于抑制状态,即yi为正yj为负,那么Wij将变小。
(4) 有导师学习算法:Delta学习规则
Delta学习规则是一种简单的有导师学习算法,该算法根据神经元的实际输出与期望输出差别来调整连接权,其数学表示如下:
![]()
其中Wij表示神经元j到神经元i的连接权,di是神经元i的期望输出,yi是神经元i的实际输出,xj表示神经元j状态,若神经元j处于激活态则xj为1,若处于抑制状态则xj为0或-1(根据激活函数而定)。a是表示学习速度的常数。假设xi为1,若di比yi大,那么Wij将增大,若di比yi小,那么Wij将变小。
Delta规则简单讲来就是:若神经元实际输出比期望输出大,则减小所有输入为正的连接的权重,增大所有输入为负的连接的权重。反之,若神经元实际输出比期望输出小,则增大所有输入为正的连接的权重,减小所有输入为负的连接的权重。这个增大或减小的幅度就根据上面的式子来计算。
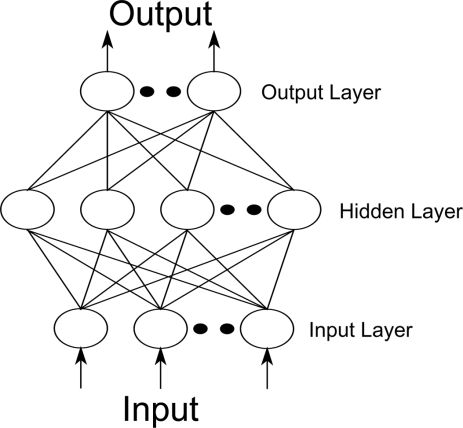
(5)有导师学习算法:BP算法
采用BP学习算法的前馈型神经网络通常被称为BP网络。
图8. 三层BP神经网络结构
BP网络具有很强的非线性映射能力,一个3层BP神经网络能够实现对任意非线性函数进行逼近(根据Kolrnogorov定理)。一个典型的3层BP神经网络模型如图7所示。
BP网络的学习算法占篇幅较大,我打算在下一篇文章中介绍。
第二节、神经网络实现
1. 数据预处理
在训练神经网络前一般需要对数据进行预处理,一种重要的预处理手段是归一化处理。下面简要介绍归一化处理的原理与方法。
(1) 什么是归一化?
数据归一化,就是将数据映射到[0,1]或[-1,1]区间或更小的区间,比如(0.1,0.9) 。
(2) 为什么要归一化处理?
<1>输入数据的单位不一样,有些数据的范围可能特别大,导致的结果是神经网络收敛慢、训练时间长。
<2>数据范围大的输入在模式分类中的作用可能会偏大,而数据范围小的输入作用就可能会偏小。
<3>由于神经网络输出层的激活函数的值域是有限制的,因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活函数,由于S形函数的值域限制在(0,1),也就是说神经网络的输出只能限制在(0,1),所以训练数据的输出就要归一化到[0,1]区间。
<4>S形激活函数在(0,1)区间以外区域很平缓,区分度太小。例如S形函数f(X)在参数a=1时,f(100)与f(5)只相差0.0067。
(3) 归一化算法
一种简单而快速的归一化算法是线性转换算法。线性转换算法常见有两种形式:
<1>
y = ( x - min )/( max - min )
其中min为x的最小值,max为x的最大值,输入向量为x,归一化后的输出向量为y 。上式将数据归一化到 [ 0 , 1 ]区间,当激活函数采用S形函数时(值域为(0,1))时这条式子适用。
<2>
y = 2 * ( x - min ) / ( max - min ) - 1
这条公式将数据归一化到 [ -1 , 1 ] 区间。当激活函数采用双极S形函数(值域为(-1,1))时这条式子适用。
(4) Matlab数据归一化处理函数
Matlab中归一化处理数据可以采用premnmx , postmnmx , tramnmx 这3个函数。
<1> premnmx
语法:[pn,minp,maxp,tn,mint,maxt] = premnmx(p,t)
参数:
pn: p矩阵按行归一化后的矩阵
minp,maxp:p矩阵每一行的最小值,最大值
tn:t矩阵按行归一化后的矩阵
mint,maxt:t矩阵每一行的最小值,最大值
作用:将矩阵p,t归一化到[-1,1] ,主要用于归一化处理训练数据集。
<2> tramnmx
语法:[pn] = tramnmx(p,minp,maxp)
参数:
minp,maxp:premnmx函数计算的矩阵的最小,最大值
pn:归一化后的矩阵
作用:主要用于归一化处理待分类的输入数据。
<3> postmnmx
语法: [p,t] = postmnmx(pn,minp,maxp,tn,mint,maxt)
参数:
minp,maxp:premnmx函数计算的p矩阵每行的最小值,最大值
mint,maxt:premnmx函数计算的t矩阵每行的最小值,最大值
作用:将矩阵pn,tn映射回归一化处理前的范围。postmnmx函数主要用于将神经网络的输出结果映射回归一化前的数据范围。
2. 使用Matlab实现神经网络
使用Matlab建立前馈神经网络主要会使用到下面3个函数:
newff :前馈网络创建函数
train:训练一个神经网络
sim :使用网络进行仿真
下面简要介绍这3个函数的用法。
(1) newff函数
<1>newff函数语法
newff函数参数列表有很多的可选参数,具体可以参考Matlab的帮助文档,这里介绍newff函数的一种简单的形式。
语法:net = newff ( A, B, {C} ,‘trainFun’)
参数:
A:一个n×2的矩阵,第i行元素为输入信号xi的最小值和最大值;
B:一个k维行向量,其元素为网络中各层节点数;
C:一个k维字符串行向量,每一分量为对应层神经元的激活函数;
trainFun :为学习规则采用的训练算法。
<2>常用的激活函数
常用的激活函数有:
a) 线性函数 (Linear transfer function)
f(x) = x
该函数的字符串为’purelin’。
b) 对数S形转移函数( Logarithmic sigmoid transfer function )
该函数的字符串为’logsig’。
c) 双曲正切S形函数 (Hyperbolic tangent sigmoid transfer function )
也就是上面所提到的双极S形函数。
该函数的字符串为’ tansig’。
Matlab的安装目录下的toolbox\nnet\nnet\nntransfer子目录中有所有激活函数的定义说明。
<3>常见的训练函数
常见的训练函数有:
traingd :梯度下降BP训练函数(Gradient descent backpropagation)
traingdx :梯度下降自适应学习率训练函数
<4>网络配置参数
一些重要的网络配置参数如下:
net.trainparam.goal :神经网络训练的目标误差
net.trainparam.show : 显示中间结果的周期
net.trainparam.epochs :最大迭代次数
net.trainParam.lr : 学习率
(2) train函数
网络训练学习函数。
语法:[ net, tr, Y1, E ] = train( net, X, Y )
参数:
X:网络实际输入
Y:网络应有输出
tr:训练跟踪信息
Y1:网络实际输出
E:误差矩阵
(3) sim函数
语法:Y=sim(net,X)
参数:
net:网络
X:输入给网络的K×N矩阵,其中K为网络输入个数,N为数据样本数
Y:输出矩阵Q×N,其中Q为网络输出个数
(4) Matlab BP网络实例
我将Iris数据集分为2组,每组各75个样本,每组中每种花各有25个样本。其中一组作为以上程序的训练样本,另外一组作为检验样本。为了方便训练,将3类花分别编号为1,2,3 。
使用这些数据训练一个4输入(分别对应4个特征),3输出(分别对应该样本属于某一品种的可能性大小)的前向网络。
Matlab程序如下:
%
读取训练数据 [f1,f2,f3,f4,class]
=
textread(
'
trainData.txt
'
,
'
%f%f%f%f%f
'
,
150
);
%
特征值归一化 [input,minI,maxI]
=
premnmx( [f1 , f2 , f3 , f4 ]
'
) ;
%
构造输出矩阵 s
=
length( class
) ; output
=
zeros( s ,
3
) ;
for
i
=
1
: s output( i , class( i ) )
=
1
; end
%
创建神经网络 net
=
newff( minmax(input) , [
10
3
] , {
'
logsig
'
'
purelin
'
} ,
'
traingdx
'
) ;
%
设置训练参数 net.trainparam.show
=
50
; net.trainparam.epochs
=
500
; net.trainparam.goal
=
0.01
; net.trainParam.lr
=
0.01
;
%
开始训练 net
=
train( net, input , output
'
) ;
%
读取测试数据 [t1 t2 t3 t4 c]
=
textread(
'
testData.txt
'
,
'
%f%f%f%f%f
'
,
150
);
%
测试数据归一化 testInput
=
tramnmx ( [t1,t2,t3,t4]
'
, minI, maxI ) ;
%
仿真 Y
=
sim( net , testInput )
%
统计识别正确率 [s1 , s2]
=
size( Y ) ; hitNum
=
0 ;
for
i
=
1
: s2 [m , Index]
=
max( Y( : , i ) ) ;
if
( Index
==
c(i) ) hitNum
=
hitNum
+
1
; end end sprintf(
'
识别率是 %3.3f%%
'
,
100
*
hitNum
/
s2 )
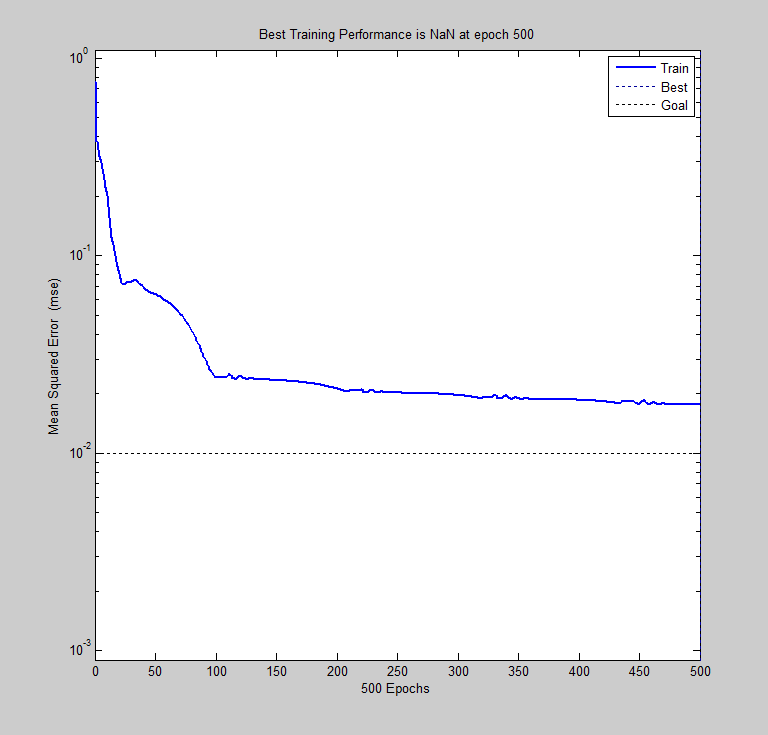
以上程序的识别率稳定在95%左右,训练100次左右达到收敛,训练曲线如下图所示:
图9. 训练性能表现
(5)参数设置对神经网络性能的影响
我在实验中通过调整隐含层节点数,选择不通过的激活函数,设定不同的学习率,
<1>隐含层节点个数
隐含层节点的个数对于识别率的影响并不大,但是节点个数过多会增加运算量,使得训练较慢。
<2>激活函数的选择
激活函数无论对于识别率或收敛速度都有显著的影响。在逼近高次曲线时,S形函数精度比线性函数要高得多,但计算量也要大得多。
<3>学习率的选择
学习率影响着网络收敛的速度,以及网络能否收敛。学习率设置偏小可以保证网络收敛,但是收敛较慢。相反,学习率设置偏大则有可能使网络训练不收敛,影响识别效果。
3. 使用AForge.NET实现神经网络
(1) AForge.NET简介
AForge.NET是一个C#实现的面向人工智能、计算机视觉等领域的开源架构。AForge.NET源代码下的Neuro目录包含一个神经网络的类库。
AForge.NET主页:http://www.aforgenet.com/
AForge.NET代码下载:http://code.google.com/p/aforge/
Aforge.Neuro工程的类图如下:
图10. AForge.Neuro类库类图
下面介绍图9中的几个基本的类:
Neuron — 神经元的抽象基类
Layer — 层的抽象基类,由多个神经元组成
Network —神经网络的抽象基类,由多个层(Layer)组成
IActivationFunction - 激活函数(activation function)的接口
IUnsupervisedLearning - 无导师学习(unsupervised learning)算法的接口ISupervisedLearning - 有导师学习(supervised learning)算法的接口
(2)使用Aforge建立BP神经网络
使用AForge建立BP神经网络会用到下面的几个类:
<1> SigmoidFunction : S形神经网络
构造函数:public SigmoidFunction( double alpha )
参数alpha决定S形函数的陡峭程度。
<2> ActivationNetwork :神经网络类
构造函数:
public ActivationNetwork( IActivationFunction function, int inputsCount, params int[] neuronsCount )
: base( inputsCount, neuronsCount.Length )
public virtual double[] Compute( double[] input )
参数意义:
inputsCount:输入个数
neuronsCount :表示各层神经元个数
<3> BackPropagationLearning:BP学习算法
构造函数:
public BackPropagationLearning( ActivationNetwork network )
参数意义:
network :要训练的神经网络对象
BackPropagationLearning类需要用户设置的属性有下面2个:
learningRate :学习率
momentum :冲量因子
下面给出一个用AForge构建BP网络的代码。
// 创建一个多层神经网络,采用S形激活函数,各层分别有4,5,3个神经元
//(其中4是输入个数,3是输出个数,5是中间层结点个数) ActivationNetwork network = new ActivationNetwork( new SigmoidFunction(2), 4, 5, 3); // 创建训练算法对象 BackPropagationLearning teacher = new BackPropagationLearning(network); // 设置BP算法的学习率与冲量系数 teacher.LearningRate = 0.1; teacher.Momentum = 0; int iteration = 1 ; // 迭代训练500次 while( iteration < 500 ) { teacher.RunEpoch( trainInput , trainOutput ) ; ++iteration ; } //使用训练出来的神经网络来分类,t为输入数据向量 network.Compute(t)[0]
改程序对Iris 数据进行分类,识别率可达97%左右 。
点击下载源代码
文章来自:http://www.cnblogs.com/heaad/
转载请保留出处,thx!
参考文献
[1] Andrew Kirillov. Neural Networks on C#. [Online].
http://www.codeproject.com/KB/recipes/aforge_neuro.aspx 2006.10
[2] Sacha Barber. AI : Neural Network for beginners. [Online].
http://www.codeproject.com/KB/recipes/NeuralNetwork_1.aspx 2007.5
[3] Richard O. Duda, Peter E. Hart and David G. Stork. 模式分类. 机械工业出版社. 2010.4
[4] Wikipedia. Iris flower data set. [Online].
http://en.wikipedia.org/wiki/Iris_flower_data_set