Stree 解题报告
Stree
题目描述
给出n个点,m条有权边,现对于每一条边,你需要回答出包含这条边的最小生成树的总边权值。
输入格式
第一行两个数n,m
接下来m行i,j,k,表示i与j间有一条权值为k的边
输出格式
m行答案。
样例输入
5 7
1 2 3
1 3 1
1 4 5
2 3 2
2 5 3
3 4 2
4 5 4
样例输出
9
8
11
8
8
8
9
数据范围
30% n<=1000
100% n,m<=200000
题解
首先,这道题是一道码农题,根据题目给出的边,我们先构造一棵最小生成树,那么构成这个最小生成树的n-1条边对应的答案自然就是这个生成树的边权和 S ,这样,我们就解决了n-1个询问。
那么,关于剩下的边的询问怎么算答案呢?
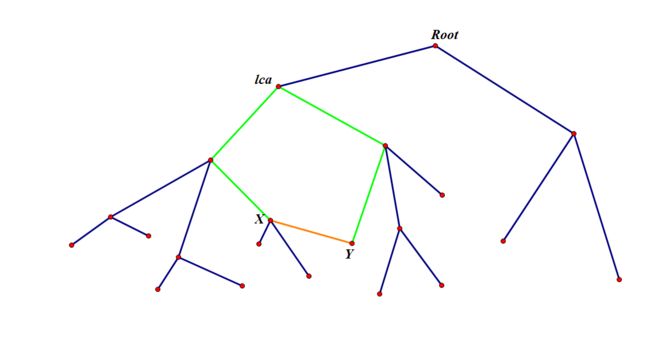
假设我们构造的最小生成树如下,我们将要进行的询问的边为(X,Y)
如果,我们选择(X,Y)这条边,那么此最小生成树便会变成一个环上上很多棵树的图。
就如下图:
绿色的边加上橙色的边(边XY)构成的即为环,不能看出绿色的边即为点X和点Y到他们的lca(最近公共祖先)的路径,然后我们的目标就是在路径上删掉一条边,使得此图再次成为一棵树,为了使答案最优,我们要选一条边权最大的边作为被删的边,用倍增算法求lca,在求lca的时候顺带记录一下跳过的那些边权的最大值即可。
那么答案即为 S + cost ( X , Y )- edge weightmax
Code(Pascal)
var
bz:array[0..200010] of boolean;
fa,en,sd:array[0..200010] of longint;
f,mx:array[0..200010,0..20] of int64;
bj:array[0..400010,1..3] of int64;
yb:array[0..400010,1..4] of int64;
tj:array[0..200010] of int64;
n,m,j,k,l,i,o,p,f1,f2,jx:longint;
ans:int64;
function max(a,b:int64):int64;
begin
if a>b then exit(a)
else exit(b);
end;
function min(a,b:int64):int64;
begin
if a<b then exit(a)
else exit(b);
end;
function search(o:longint):longint;
begin
if fa[o]=o then exit(o);
fa[o]:=search(fa[o]);
exit(fa[o]);
end;
procedure qsortyb(l,r:longint);
var
i,j:longint;
m:int64;
begin
i:=l;
j:=r;
m:=yb[(l+r) div 2,3];
repeat
while yb[i,3]<m do inc(i);
while yb[j,3]>m do dec(j);
if i<=j then
begin
yb[0]:=yb[i];
yb[i]:=yb[j];
yb[j]:=yb[0];
inc(i);
dec(j);
end;
until i>j;
if l<j then qsortyb(l,j);
if i<r then qsortyb(i,r);
end;
procedure add(X,Y,Z:INT64);
begin
inc(en[x]);
inc(en[y]);
inc(o);
bj[o,1]:=x;
bj[o,2]:=y;
bj[o,3]:=z;
inc(o);
bj[o,1]:=y;
bj[o,2]:=x;
bj[o,3]:=z;
end;
procedure bh;
var
i,k:longint;
begin
randomize;
for i:=1 to o div 2 do
begin
k:=i+random(o div 2);
bj[0]:=bj[k];
bj[k]:=bj[i];
bj[i]:=bj[0];
end;
end;
procedure qsort(l,r:longint);
var
i,j,m:longint;
begin
i:=l;
j:=r;
m:=bj[(l+r) div 2,1];
repeat
while bj[i,1]<m do inc(i);
while bj[j,1]>m do dec(j);
if i<=j then
begin
bj[0]:=bj[i];
bj[i]:=bj[j];
bj[j]:=bj[0];
inc(i);
dec(j);
end;
until i>j;
if l<j then qsort(l,j);
if i<r then qsort(i,r);
end;
procedure dg(o:longint);
var
i,j,m:longint;
begin
j:=0;
while f[f[o,j],j]>0 do
begin
f[o,j+1]:=f[f[o,j],j];
mx[o,j+1]:=max(mx[o,j],mx[f[o,j],j]);
inc(j);
end;
for i:=en[o-1]+1 to en[o] do
if bj[i,2]<>f[o,0] then
begin
f[bj[i,2],0]:=o;
mx[bj[i,2],0]:=bj[i,3];
sd[bj[i,2]]:=sd[o]+1;
dg(bj[i,2]);
end;
end;
function xz(x,y:longint):int64;
var
k:longint;
p:int64;
begin
k:=jx;
p:=0;
if sd[x]<sd[y] then
while k>=0 do
begin
if sd[f[y,k]]>=sd[x] then
begin
p:=max(p,mx[y,k]);
y:=f[y,k];
end;
dec(k);
end;
if sd[x]>sd[y] then
while k>=0 do
begin
if sd[f[x,k]]>=sd[y] then
begin
p:=max(p,mx[x,k]);
x:=f[x,k];
end;
dec(k);
end;
k:=jx;
while (k>=0) do
begin
if f[x,k]<>f[y,k] then
begin
p:=max(p,mx[x,k]);
p:=max(p,mx[y,k]);
x:=f[x,k];
y:=f[y,k];
end;
dec(k);
end;
while x<>y do
begin
p:=max(p,mx[x,0]);
p:=max(p,mx[y,0]);
x:=f[x,0];
y:=f[y,0];
end;
exit(p);
end;
begin
assign(input,'street.in'); reset(input);
assign(output,'street.out'); rewrite(output);
readln(n,m);
jx:=min(20,trunc(ln(n)/ln(2))+1);
for i:=1 to m do
begin
readln(yb[i,1],yb[i,2],yb[i,3]);
yb[i,4]:=i;
end;
for i:=1 to n do
fa[i]:=i;
qsortyb(1,m);
ans:=0;
for i:=1 to m do
if search(yb[i,1])<>search(yb[i,2]) then
begin
f1:=search(yb[i,1]);
f2:=search(yb[i,2]);
fa[f2]:=f1;
ans:=ans+yb[i,3];
add(yb[i,1],yb[i,2],yb[i,3]);
bz[i]:=true;
end;
for i:=1 to n do
en[i]:=en[i-1]+en[i];
bh;
qsort(1,o);
sd[1]:=1;
dg(1);
for i:=1 to m do
if bz[i] then tj[yb[i,4]]:=ans
else tj[yb[i,4]]:=ans+yb[i,3]-xz(yb[i,1],yb[i,2]);
for i:=1 to m do
writeln(tj[i]);
close(input);
close(output);
end.