一个简单的网络系统可以被描述成一棵无根树。每个节点为一个服务器。连接服务器与服务器的数据线则看做
一条树边。两个服务器进行数据的交互时，数据会经过连接这两个服务器的路径上的所有服务器（包括这两个服务
器自身）。由于这条路径是唯一的，当路径上的某个服务器出现故障，无法正常运行时，数据便无法交互。此外，
每个数据交互请求都有一个重要度，越重要的请求显然需要得到越高的优先处理权。现在，你作为一个网络系统的
管理员，要监控整个系统的运行状态。系统的运行也是很简单的，在每一个时刻，只有可能出现下列三种事件中的
一种：1. 在某两个服务器之间出现一条新的数据交互请求；2. 某个数据交互结束请求；3. 某个服务器出现故
障。系统会在任何故障发生后立即修复。也就是在出现故障的时刻之后，这个服务器依然是正常的。但在服务器产
生故障时依然会对需要经过该服务器的数据交互请求造成影响。你的任务是在每次出现故障时，维护未被影响的请
求中重要度的最大值。注意，如果一个数据交互请求已经结束，则不将其纳入未被影响的请求范围。
bzoj4538【HNOI2016】网络
4538: [Hnoi2016]网络
Time Limit: 20 Sec Memory Limit: 128 MBSubmit: 651 Solved: 300
[ Submit][ Status][ Discuss]
Description
Input
第一行两个正整数n,m，分别描述服务器和事件个数。服务器编号是从1开始的，因此n个服务器的编号依次是1
,2,3,…,n。接下来n-1行，每行两个正整数u,v，描述一条树边。u和v是服务器的编号。接下来m行，按发生时刻依
次描述每一个事件；即第i行（i=1,2,3,…,m）描述时刻i发生的事件。每行的第一个数type描述事件类型，共3种
类型：（1）若type=0，之后有三个正整数a,b,v，表示服务器a,b之间出现一条重要度为v的数据交互请求；（2）
若type=1，之后有一个正整数t，表示时刻t（也就是第t个发生的事件）出现的数据交互请求结束；（3）若type=2
，之后有一个正整数x，表示服务器x在这一时刻出现了故障。对于每个type为2的事件，就是一次询问，即询问“
当服务器x发生故障时，未被影响的请求中重要度的最大值是多少？”注意可能有某个服务器自身与自身进行数据
交互的情况。2 ≤ n ≤ 10^5, 1 ≤ m ≤ 2×10^5，其他的所有输入值不超过 10^9
Output
对于每个type=2的事件，即服务器出现故障的事件，输出一行一个整数，描述未被影响的请求中重要度的最大
值。如果此时没有任何请求，或者所有请求均被影响，则输出-1。
Sample Input
13 23
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
6 10
6 11
7 12
7 13
2 1
0 8 13 3
0 9 12 5
2 9
2 8
2 2
0 10 12 1
2 2
1 3
2 7
2 1
0 9 5 6
2 4
2 5
1 7
0 9 12 4
0 10 5 7
2 1
2 4
2 12
1 2
2 5
2 3
1 2
1 3
2 4
2 5
3 6
3 7
4 8
4 9
6 10
6 11
7 12
7 13
2 1
0 8 13 3
0 9 12 5
2 9
2 8
2 2
0 10 12 1
2 2
1 3
2 7
2 1
0 9 5 6
2 4
2 5
1 7
0 9 12 4
0 10 5 7
2 1
2 4
2 12
1 2
2 5
2 3
Sample Output
-1
3
5
-1
1
-1
1
1
3
6
7
7
4
6
3
5
-1
1
-1
1
1
3
6
7
7
4
6
HINT
样例给出的树如下所示：
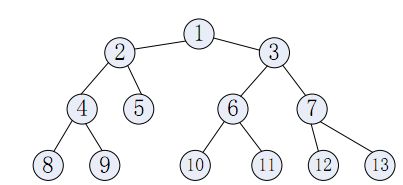
解释其中的部分询问；下面的解释中用(a,b;t,v)表示在t时刻出现的服务器a和b之间的重
要度为v的请求：
对于第一个询问（在时刻1），此时没有任何请求，输出-1。
对于第四个询问（在时刻6），此时有两条交互(8,13;2,3),(9,12;3,5)，所有询问均经过2
号服务器，输出-1。
对于第五个询问（在时刻8），此时有三条交互(8,13;2,3),(9,12;3,5),(10,12;7,1)，只有交互
(10,12;7,1)没有经过2号服务器，因此输出其重要度1。
对于最后一个询问（在时刻23），此时有三条交互(9,5;12,6),(9,12;16,4),(10,5;17,7)。当3
号服务器出现故障时，只有交互(9,5;12,6)没有经过3号服务器，因此输出6。
2016.5.20新加数据一组,未重测
方法一：二分答案+线段树
相当于是求不包含一个点的所有链中的最大权值。
二分一个权值，询问权值大于它的链的交集是否包含这个点。
于是问题就转化为如何求链的交集。
用线段树维护链的交集，每个点表示权值在这个区间内的链的交集，在线段树上二分答案即可。预处理ST表，每次O(1)求LCA、O(1)求链的交集。
代码：http://www.cnblogs.com/Ngshily/p/5413933.html
方法二：树链剖分+线段树
线段树每个节点维护一个堆，保存不经过这段路径的链的权值信息。（这个思路很棒！！！）
对于一个询问，把包含这个点的所有线段所对应堆的最大值取max既可以了。
这里有一个比较极值的堆的写法：用两个优先队列就可以搞定，一个表示插入、一个表示删除。询问堆顶元素的时候，不停弹出两个优先队列的队首元素，直到两个队首元素不同。
然后写完就发现MLE，艾玛这题丧心病狂到卡内存...看discuss发现在求重儿子的时候把>改成>=就过了......=_=服了
代码：
#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#include<queue>
#define F(i,j,n) for(int i=j;i<=n;i++)
#define D(i,j,n) for(int i=j;i>=n;i--)
#define ll long long
#define pa pair<int,int>
#define N 100005
using namespace std;
int n,m,cnt,tot;
int head[N],d[N],fa[N],sz[N],son[N],pos[N],top[N];
pa p[N];
struct edge{int next,to;}e[N*2];
struct data{int a,b,v;}q[N*2];
struct Heap
{
priority_queue<int> a,b;
void add(int x){a.push(x);}
void del(int x){b.push(x);}
int top()
{
while (!b.empty()&&a.top()==b.top()) a.pop(),b.pop();
return a.empty()?-1:a.top();
}
}t[N*4];
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
inline void add_edge(int x,int y)
{
e[++cnt]=(edge){head[x],y};head[x]=cnt;
e[++cnt]=(edge){head[y],x};head[y]=cnt;
}
void dfs1(int x,int f)
{
fa[x]=f;d[x]=d[f]+1;sz[x]=1;son[x]=0;
for(int i=head[x];i;i=e[i].next)
{
int y=e[i].to;
if (y!=f)
{
dfs1(y,x);
sz[x]+=sz[y];
if (sz[y]>=sz[son[x]]) son[x]=y;//这里写>=可以过，写>就会MLE，别问我为什么
}
}
}
void dfs2(int x,int chain)
{
pos[x]=++tot;top[x]=chain;
if (son[x]) dfs2(son[x],chain);
for(int i=head[x];i;i=e[i].next)
{
int y=e[i].to;
if (y!=fa[x]&&y!=son[x]) dfs2(y,y);
}
}
void change(int k,int l,int r,int L,int R,int val,int flg)
{
if (l==L&&r==R)
{
if (flg) t[k].add(val);
else t[k].del(val);
return;
}
int mid=(l+r)>>1;
if (R<=mid) change(k<<1,l,mid,L,R,val,flg);
else if (L>mid) change(k<<1|1,mid+1,r,L,R,val,flg);
else change(k<<1,l,mid,L,mid,val,flg),change(k<<1|1,mid+1,r,mid+1,R,val,flg);
}
void solve(int x,int y,int val,int flg)
{
int tot=0;
while (top[x]!=top[y])
{
if (d[top[x]]<d[top[y]]) swap(x,y);
p[++tot]=make_pair(pos[top[x]],pos[x]);
x=fa[top[x]];
}
if (d[x]>d[y]) swap(x,y);
p[++tot]=make_pair(pos[x],pos[y]);
sort(p+1,p+tot+1);
p[0]=make_pair(0,0);
p[tot+1]=make_pair(n+1,n+1);
F(i,0,tot)
{
int l=p[i].second+1,r=p[i+1].first-1;
if (l<=r) change(1,1,n,l,r,val,flg);
}
}
int query(int k,int l,int r,int x)
{
if (l==r) return t[k].top();
int mid=(l+r)>>1;
if (x<=mid) return max(t[k].top(),query(k<<1,l,mid,x));
else return max(t[k].top(),query(k<<1|1,mid+1,r,x));
}
int main()
{
n=read();m=read();
F(i,1,n-1){int x=read(),y=read();add_edge(x,y);}
dfs1(1,0);dfs2(1,1);
F(i,1,m)
{
int opt=read(),x;
if (opt==0)
{
q[i].a=read();q[i].b=read();q[i].v=read();
solve(q[i].a,q[i].b,q[i].v,1);
}
else if (opt==1){x=read();solve(q[x].a,q[x].b,q[x].v,0);}
else{x=read();printf("%d\n",query(1,1,n,pos[x]));}
}
return 0;
}