BZOJ2301 [HAOI2011]Problem b(莫比乌斯反演)
莫比乌斯反演的一些东西:
莫比乌斯反演定理
或
莫比乌斯函数:
【题解】
用容斥的思想:
Ans( a<=x<=b , c<=y<=d ) = Ans( 1<=x<=b , 1<=y<=d ) - Ans( 1<=x<=a-1 , 1<=y<=d ) - Ans( 1<=x<=b , 1<=y<=c-1 ) + Ans( 1<=x<=a-1 , 1<=y<=c-1 )
那么对于转化后的每个询问:1<=x<=n,1<=y<=m,gcd(x,y)=k的(x,y)个数
设f(k)为答案,F(k)表示 1<=x<=n,1<=y<=m,k|gcd(x,y)的(x,y)个数,则:
F(k)=sigma( f(d) ) , k|d,又 F(k)=[n/k]*[m/k]
=> f(k)=sigma( mu(d/k)*F(d) ) , k|d
=sigma( mu(d/k)*[n/d]*[m/d] ) , k|d
直接枚举d,复杂度为线性,会超时
而对于某些d,[n/d1]=[n/d2],[n/d]最多有2*sqrt(n)个取值
那么 [n/d]*[m/d]最多有 2*sqrt(n)+2*sqrt(m) 个取值
枚举d时,计算出 d2>=d 且 [n/d2]*[m/d2]=[n/d]*[m/d] 的最大d2值,d与d2之间的的都不改变F值,直接跳过即可,前缀和处理mu[]
复杂度为O(n*sqrt(n))
【代码】
#include<stdio.h>
#include<stdlib.h>
typedef long long LL;
int no[50005],pri[50005],mu[50005];
int k;
int min(int a,int b)
{
if(a<b) return a;
return b;
}
LL ask(int n,int m)
{
LL ans=0;
int i,last;
for(i=1;i*k<=n&&i*k<=m;i=last+1)//枚举:d=i*k
{
last=min( n/(n/(i*k)) , m/(m/(i*k)) )/k;// i*k~last*k 代入 d:[n/d]*[m/d]均不变
ans+=(LL)(mu[last]-mu[i-1])*(LL)(n/(i*k))*(LL)(m/(i*k));
}
return ans;
}
int main()
{
int n,a,b,c,d,i,j,p=0;
scanf("%d",&n);
mu[1]=1;
for(i=2;i<=50000;i++)
{
if(no[i]==0)
{
pri[++p]=i;
mu[i]=-1;
}
for(j=1;j<=p&&pri[j]*i<=50000;j++)
{
no[pri[j]*i]=1;
if(i%pri[j]==0) break;
mu[pri[j]*i]=-mu[i];
}
}
for(i=2;i<=50000;i++)
mu[i]+=mu[i-1];
for(;n>0;n--)
{
scanf("%d%d%d%d%d",&a,&b,&c,&d,&k);
printf("%lld\n",ask(b,d)-ask(a-1,d)-ask(b,c-1)+ask(a-1,c-1));
}
return 0;
}
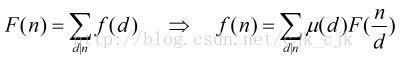
![BZOJ2301 [HAOI2011]Problem b(莫比乌斯反演)_第1张图片](http://img.e-com-net.com/image/info5/44af5590eab44e27a13c27310cde1eda.jpg)