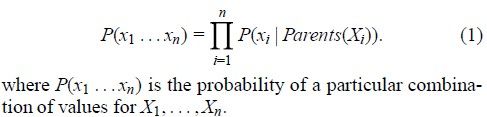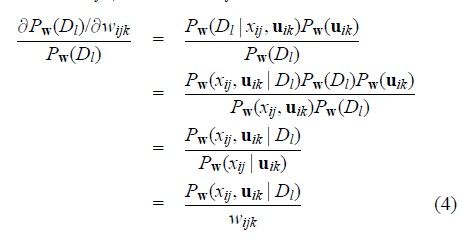论文读书笔记-local learning in probabilistic networks with hidden variables

 

标题：local learning in probabilistic networks with hidden variables

这篇论文是介绍人工智能中概率的，提到了贝叶斯信念网，APN等等，和书上内容较为接近。下面是摘抄的一些要点：

1、一些概念介绍

neuralnetworks,which represent complex input/output relations using combinations ofsimple nonlinear processing elements, are a familiar tool in AI andcomputational neuroscience.

Probabilisticnetworks(also called belief networks or Bayesian networks) are a more explicitrepresentation of the joint probability distribution characterizing a problemdomain, providing a topological description of the causal relationships amongvariables.

从这两段文字中就能体会到神经网络和信念网之间的区别和联系

Computationalmodels in AI are judged by two main criteria:ease of creation and effectivenessin decision making.这句话指出了在AI领域如何评价一个计算模型的好坏。

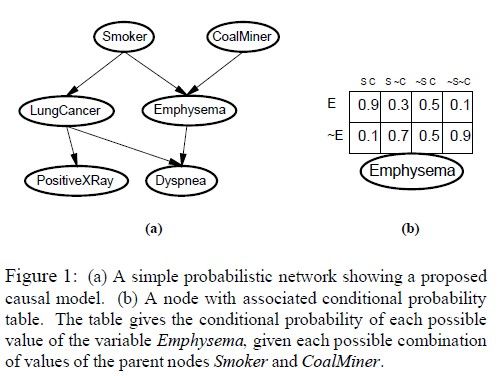
Probalilitytheory views the world as a set of random variables X1…Xn, each of which has adomain of possible values. The key concept in probability theory is the jointprobability distribution, which specifies a probability for each possiblecombination of values for all the random variables.这段话指出了各个变量直接的联系关系，下面所示的贝叶斯信念网就是这种联系的形象化体现：

Formally,a probabilistic network is defined by a directed acyclic graph together with aconditional probability table(CPT) associated with each node. The CPTassociated with variable X specifies the conditional distributionP(X|Parents(X)).

比较重要的还是下面这个式子：

 

2、learning probabilistic networks

从上面的贝叶斯信念网可以看到只有知道了拓扑结构和变量的个数才能形成网络。但是有时候这些往往是不全知道的，主要有下面几种情况：

l  知道了网络结构和全部可观察的变量，这时我们只需要学习CPT中值即可，这个较为简单。

l  不知道网络结构但是知道全部可观察变量，这时需要构造网络的拓扑结构，用到的算法一般是贪心，这个较为复杂

l  结构知道但是存在不知道的隐藏变量，这就是这篇论文要解决的问题，这些隐藏变量往往不能忽视，如果删去就会给网络增加复杂度，如下图所示：

最终问题表述如下：

Thealgorithm is provided with a network structure and initial (randomly generated)values for the CPTs. It is presented with a set D of data cases D1, . . . ,Dm. Theobject is to find the CPT parameters w that best model the data. We adopt aBayesian notion of “best.” More specifically, we assume that each possible settingof w is equally likely a priori, so that the maximum likelihood model isappropriate. This means that the aim is to maximize Pw(D), the probabilityassigned by the network to the observed data when the CPT parameters are set tow.

可以看出，最终就是要最大化Pw(D)值，为此可以采用梯度下降的算法，在每个w处计算梯度向量，然后沿着梯度向量方向进行变化，设定一个步长值。当梯度向量变成0时，就达到了局部最大值。

In ourderivation, we will use the standard notation wijk to denote a specific CPTentry, the probability that variable Xi takes on its jth possible valueassignment given that its parents Ui take on their kth possible valueassignment:

注意到由于wijk是线性的，只出现在j,k指定的位置上，故Pw(xij’|uik’)=wijk，得到：

这样就得到了我们需要的梯度值，给出每一个集合D，都需要计算Pw(xij,uik|Dl)值。

 

小结：这篇文章中其实就是把神经网络的梯度下降的方法应用到贝叶斯信念网求解中，当然前提是发现这两种网络的相同和区别，正如作者在文中说的那样神经网络中还有BP方法，但是放在这里却不是很合适，显然这就是这两种网络不同点所造成的。