最短路径算法正确性和操作性闲杂谈-Dijkstra&Floyd算法
今天在帮圈子里一位朋友规划第七层网络路径规划的时候,又一次遇到了最短路径算法的问题,我不想在这里贴Dijkstra算法或者Floyd算法的源码,也不想去刻意分辨什么动态规划和贪心算法的联系和区别,只是闲来记录几笔而已。鉴于之前写了很多关于TCP/IP网络的文章且专业性都比较强,自然的,其可读性和可查阅性就会很弱,所以,关于本文,我想写的随意一些。
-----------------------------------
2009年,由于工作原因第一次用到了Dijkstra算法,非常顺利,直接在网上找了一段代码...但是我下班后却没有直接回家,而是直接跑去了上海书城五楼东北角的书架上再次翻阅了一本关于算法的书,寻找Dijkstra算法正确性的证明。之所以我知道这本书里有这个证明并且能在正确的位置找到它,原因不外乎以下两点:第一,我之前看到过这个证明,但是由于没有真正用到,所以一扫而过,第二,这种问题足够重要但关注的人又比较少,所以那本书可以一直在那里而不被下架或者售罄。
好吧,我承认那个时候我真正看懂了Dijkstra算法的证明,并且在几年后的2015年的一天由于又一次遇到了相关的问题还写了一篇博客。今天,当我再次遇到相关问题的时候,我自然而然地又一次想起了上海书城和我的那篇博客,但我首先已经不可能再跑去上海书城了,我目前人在深圳...再看那篇博客,我发现写的是如此乱七八糟,以至于我想删掉它!所以,我想再来一篇!
我们需要求的是从S到D的最短路径,怎么证明按照Dijkstra算法一步步操作,最终的结果就一定正确呢?其实很简单,我也不再去扯什么数学归纳法之类的了,我试着用平和的自然语言去阐述这个问题。
首先我们要承认从S到D的最短路径是一定存在的,然后我们用执果溯因法,假设已经找到了这条路径,它是S-a-b-c-d-e-...-D。那么以下结论是可以证明的,那就是:
S到a的最短路径就是S-a;
S到b的最短路径就是S-a-b
S到c的最短路径就是S-a-b-c
...
想证明以上这些非常简单,那就是利用松弛算法,假设S到a的最短路径不是S-a,而是经过了其它的节点,比如A',那么很显然S-A'-a的长度小于S-a,因此就会得出从S到D的最短路径是S-A'-a-b-c-d-e-...-D而不是S-a-b-c-d-e-...-D,这与假设是违背的。
类似的,我们可以证明以上其它的结论也是正确的。
接下来的结论就是,只要按照最短路径每次加进一段,当这些路径中节点包含D的时候,就可以坚定地说,我找到了从S到D的最短路径。现在的问题是,如何证明Dijkstra算法每次加入的那个节点x算出的从S到x的距离就是S到x的最短距离。
这也很简单,假设不是最短距离会怎样呢?也就是说,如果x通过另一个节点y到达S的距离更短,会怎样呢?如果这样的话,Dijkstra算法根本就不会选择x加入已经确定的集合,而会选择y节点加入,所以这是矛盾的!
...
把一个复杂的全局性的问题,执果溯因法分解到简单的单体问题,然后只需证明算法针对单体问题是正确的,就一切OK了。
我觉得,我以上的解释要比之前那篇证明Dijkstra算法正确性的博客更加容易理解吧。
不!决不!
接下来的篇幅交给另一个算法,即Floyd算法。这次,我只谈操作性,不谈证明。
事实上,我并没刻意去区分Floyd算法和Dijkstra算法,它们本质上是一样的东西,都是局部决定整体思想下的结果。

这个Floyd算法是个典型的Step by Step的算法步骤,非常适合计算机硬件去实现,但是相对于单源Dijkstra算法,其时间复杂度是立方级的O(n^3),对于路由器而言,这实则压力不小,反观Dijkstra算法则更适合路由器,因为IP网络是逐跳转发的,路由器只用操心以自己为源点到达其它任意节点的最短距离即可。
-----------------------------------
帮朋友做的这个事涉及到了一些地图和导航的东西,第七层路由是一个很泛的概念,你可以将它看作是任何只要不是TCP/IP或者其以下的层面的最短路径规划问题。事实上,这个所谓的第七层路由在CDN回源以及源站之间的同步方面起着很大的作用。路由本身就不单指IP路由,它的含义是”你要经由的路径“。
-----------------------------------
自小就对地图感兴趣,小时候没事就买地图册来看,只要是可以做把点用线连起来的事,我都特别感兴趣,比如说除了地图,我还喜欢针线活儿,家里大大小小的针线活都是我来做,当然,缝补是十分讲技巧的,每一个针脚都要斟酌,如何用最少的线,如何不留痕迹等等...另外,我喜欢走街窜巷,不为去什么目的地,只是走走看看但是绝对不停...后来,我接触到了图论,发现这一切的背后都是有理论基础的,这也许就是后来上学后我非常喜欢网络技术的原因吧,同时这也是我讨厌TCP的原因,因为我看不到把端节点连起来的那根线(我喜欢狮子,猎豹和猫,但我讨厌鬣狗,秃鹫和蝙蝠)。
我曾经很惊奇于自己为什么可以不用导航每次都可以在节假日避开拥堵的路段(我被家人和很多朋友称作活导航),后来我想通了,之所以我每次都可以避开拥堵,并不是因为我有什么特异功能,而是因为他们其它人大多数都使用了导航,而我要说的是,这些导航无一例外都是垃圾!我骂它们是垃圾并没有待价而沽而欲求职的念头,我现在已经有一份很好的工作,并且短期内不会更换,完全不是为了受到青睐而骂它们垃圾,这完全是因为这些导航做的本来就是垃圾!
-----------------------------------
2009年,由于工作原因第一次用到了Dijkstra算法,非常顺利,直接在网上找了一段代码...但是我下班后却没有直接回家,而是直接跑去了上海书城五楼东北角的书架上再次翻阅了一本关于算法的书,寻找Dijkstra算法正确性的证明。之所以我知道这本书里有这个证明并且能在正确的位置找到它,原因不外乎以下两点:第一,我之前看到过这个证明,但是由于没有真正用到,所以一扫而过,第二,这种问题足够重要但关注的人又比较少,所以那本书可以一直在那里而不被下架或者售罄。
好吧,我承认那个时候我真正看懂了Dijkstra算法的证明,并且在几年后的2015年的一天由于又一次遇到了相关的问题还写了一篇博客。今天,当我再次遇到相关问题的时候,我自然而然地又一次想起了上海书城和我的那篇博客,但我首先已经不可能再跑去上海书城了,我目前人在深圳...再看那篇博客,我发现写的是如此乱七八糟,以至于我想删掉它!所以,我想再来一篇!
我们需要求的是从S到D的最短路径,怎么证明按照Dijkstra算法一步步操作,最终的结果就一定正确呢?其实很简单,我也不再去扯什么数学归纳法之类的了,我试着用平和的自然语言去阐述这个问题。
首先我们要承认从S到D的最短路径是一定存在的,然后我们用执果溯因法,假设已经找到了这条路径,它是S-a-b-c-d-e-...-D。那么以下结论是可以证明的,那就是:
S到a的最短路径就是S-a;
S到b的最短路径就是S-a-b
S到c的最短路径就是S-a-b-c
...
想证明以上这些非常简单,那就是利用松弛算法,假设S到a的最短路径不是S-a,而是经过了其它的节点,比如A',那么很显然S-A'-a的长度小于S-a,因此就会得出从S到D的最短路径是S-A'-a-b-c-d-e-...-D而不是S-a-b-c-d-e-...-D,这与假设是违背的。
类似的,我们可以证明以上其它的结论也是正确的。
接下来的结论就是,只要按照最短路径每次加进一段,当这些路径中节点包含D的时候,就可以坚定地说,我找到了从S到D的最短路径。现在的问题是,如何证明Dijkstra算法每次加入的那个节点x算出的从S到x的距离就是S到x的最短距离。
这也很简单,假设不是最短距离会怎样呢?也就是说,如果x通过另一个节点y到达S的距离更短,会怎样呢?如果这样的话,Dijkstra算法根本就不会选择x加入已经确定的集合,而会选择y节点加入,所以这是矛盾的!
...
把一个复杂的全局性的问题,执果溯因法分解到简单的单体问题,然后只需证明算法针对单体问题是正确的,就一切OK了。
我觉得,我以上的解释要比之前那篇证明Dijkstra算法正确性的博客更加容易理解吧。
好了,当我们知道了Dijkstra算法是正确的,接下来呢?
-----------------------------------
不!决不!
接下来的篇幅交给另一个算法,即Floyd算法。这次,我只谈操作性,不谈证明。
事实上,我并没刻意去区分Floyd算法和Dijkstra算法,它们本质上是一样的东西,都是局部决定整体思想下的结果。
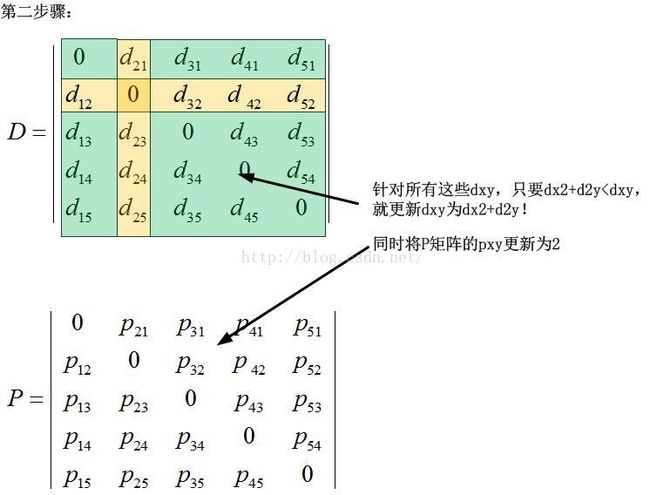
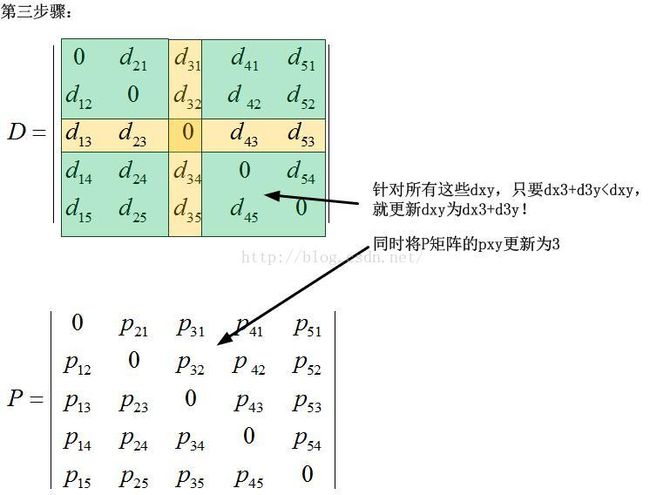
首先将一个原始图转化为以下两个矩阵,其中矩阵D表示图的邻接矩阵,而矩阵P表示图节点的经由路径:

然后操作就开始了,步骤非常之简单,我只给出前三个步骤:
这个Floyd算法是个典型的Step by Step的算法步骤,非常适合计算机硬件去实现,但是相对于单源Dijkstra算法,其时间复杂度是立方级的O(n^3),对于路由器而言,这实则压力不小,反观Dijkstra算法则更适合路由器,因为IP网络是逐跳转发的,路由器只用操心以自己为源点到达其它任意节点的最短距离即可。
-----------------------------------
帮朋友做的这个事涉及到了一些地图和导航的东西,第七层路由是一个很泛的概念,你可以将它看作是任何只要不是TCP/IP或者其以下的层面的最短路径规划问题。事实上,这个所谓的第七层路由在CDN回源以及源站之间的同步方面起着很大的作用。路由本身就不单指IP路由,它的含义是”你要经由的路径“。
-----------------------------------
自小就对地图感兴趣,小时候没事就买地图册来看,只要是可以做把点用线连起来的事,我都特别感兴趣,比如说除了地图,我还喜欢针线活儿,家里大大小小的针线活都是我来做,当然,缝补是十分讲技巧的,每一个针脚都要斟酌,如何用最少的线,如何不留痕迹等等...另外,我喜欢走街窜巷,不为去什么目的地,只是走走看看但是绝对不停...后来,我接触到了图论,发现这一切的背后都是有理论基础的,这也许就是后来上学后我非常喜欢网络技术的原因吧,同时这也是我讨厌TCP的原因,因为我看不到把端节点连起来的那根线(我喜欢狮子,猎豹和猫,但我讨厌鬣狗,秃鹫和蝙蝠)。
我曾经很惊奇于自己为什么可以不用导航每次都可以在节假日避开拥堵的路段(我被家人和很多朋友称作活导航),后来我想通了,之所以我每次都可以避开拥堵,并不是因为我有什么特异功能,而是因为他们其它人大多数都使用了导航,而我要说的是,这些导航无一例外都是垃圾!我骂它们是垃圾并没有待价而沽而欲求职的念头,我现在已经有一份很好的工作,并且短期内不会更换,完全不是为了受到青睐而骂它们垃圾,这完全是因为这些导航做的本来就是垃圾!
即便再过一年,我突然想换一份工作了,我也依然不会待价而沽,我为什么不在自己的公司的另一个部门换一个职位呢?求别骚扰!但我还是忍不住想说所有的导航都是垃圾!本来我想多写点关于导航寻址的事情的,这也不枉本文的题目,然而老婆和小小下周要回上海,周日我要陪她们,所以就不熬了。
-----------------------------------
《JAVA编程思想》里有思想吗?编程需要思想吗?难道不是照着经理的指示做就可以了吗?是的,编程不需要思想,编程只需要照着经理的指示做即可。现在,问题不在这里,现在的问题是,就算经理死了,那么《JAVA编程思想》里有思想吗?不!还是没有思想!你能在《JAVA编程思想》这本书里看到什么思想吗?除了讲语法和注意事项之外,你能看到《红楼梦》般的思想吗?不,你不能!
所以,《JAVA编程思想》没思想。Together with 温州皮鞋厂老板和经理是傻逼,被爆菊!