算法图解part4：快速排序

1.分而治之 D&C（Divide and Conquer）

百度百科
所谓“分而治之” 就是把一个复杂的算法问题按一定的“分解”方法分为等价的规模较小的若干部分，然后逐个解决，分别找出各部分的解，把各部分的解组成整个问题的解，这种朴素的思想来源于人们生活与工作的经验，也完全适合于技术领域。诸如软件的体系结构设计、模块化设计都是分而治之的具体表现。

分而治之：一种著名的递归式问题解决方法。
三个例子来引入该思想：

• 1.农场主分割田，要求将地皮均匀地分成方块，且分出的方块尽可能大；
• 2.求一个数字数组的元素之和；
• 3.快速排序

该思想的步骤：

1.找出基线条件，条件必须尽可能简单
2.不断将问题分解或者缩小规模，直到符合基线条件

D&C并非可用于解决问题的算法，而是一种解决问题的思想

1.1农场主分田

将田地均匀地分成方块，且分出去的方块要尽可能的大。
分田的例子中，将一条边是另一条边的整数倍作为基线条件，递归条件为最小边是所切割的最大正方形边。
递归条件为缩小问题范围，借鉴思想是：适用于这块小地的最大方块，也是适用于整块地的最大方块。
PS:这个思想可参考欧几里得算法

1.2数组之和

用递归的思想写出求和公式sum。具体思路如下：

• 首先确定基线条件为数组为空或者是只包含一个元素
  
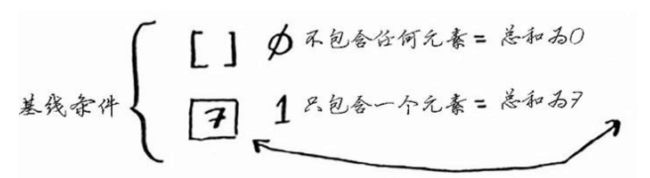
• 递归条件呢？如何把问题慢慢分解呢?数组的元素之和可以是先以某种规律，取出一个元素，再将该元素与剩下的数组之和 相加，这个新数组可以再次使用规律继续分解。。。。。。如图：
  
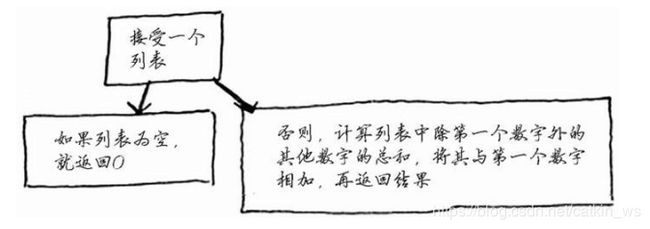
• 在解决列表[2,4,6]的和问题中，整个函数的运行过程如下：
  
  
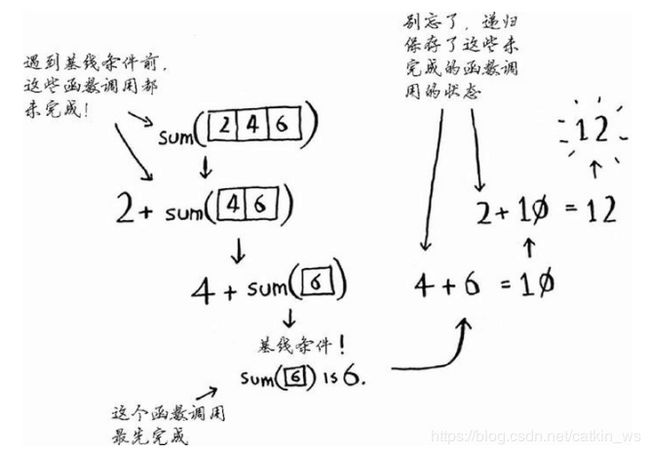
• 对上述问题的小练习（python代码）：

1.sum函数的代码：

def sum1(list):
    if list == []:
        return 0
    else:
        return list[0] + sum(list[1:])

sum1([1,2,3])

运行结果：

6

2.递归计算列表中的元素个数：

def count(list):
    if list == []:
        return 0
    else:
        return 1 + count(list[1:])

count([1,2,3])

运行结果：

3

3.递归找出最大数：

#未使用递归
def findmax(arr):
    max = arr[0]
    for i in range(1,len(arr)):
        if max < arr[i]:
            max = arr[i]
    return max

arr = [1,2,3,4,8,6,2,2]
findmax(arr)

运行结果：

8

使用递归的例子是元素数大于等于2的情况下：

#使用递归
def findvalue(list):
    if len(list) == 2:
        return list[0] if list[0] > list[1] else list[1]
    sub_max = findvalue(list[1:])
    return list[0] if list[0] > sub_max else sub_max

findvalue([1,8,3,4,5,4])

运行结果：

8

2.快速排序

还是一组数组，既然是数组，那么上述D&C讨论的基线条件也成立：当数组为空或者只有一个元素。然后递归条件使问题范围缩小，有了前文的铺垫，摘出一个元素作为基准值，当然可以是任意一个元素，我们默认第一个或者最后一个，此为递归条件。下面是快速排序的精髓：

• 1.选出基准值
• 2.将数组分成两个子数组：小于基准值的a和大于基准值的b
• 3.对剩下来的两个数组a，b进行快速排序
• 4.合并数组 a + 基准值 + b

快速排序的要点就是：找基准，分数组，小数组左边站，大数组右边站，如此往复最终完成排序。就是这么简单！

Python代码

//快速排序
def quicksort(list):
    if len(list)<2:                                    #基线条件：为空或者只包含一个元素的数组是有序的
        return list
    else:                                              #递归条件
        root = list[0]                                 #基准值
        di   = [i for i in list[1:] if i <= root]      #小于等于基准值 为di数组
        gao  = [i for i in list[1:] if i >  root]      #大于基准值为gao数组
        return quicksort(di) + [root] + quicksort(gao) #对两个数组快速排序递归，然后合并
        
quicksort([4,5,87,4,8,2,4,85,2,1,87,25,24,8,21,5,2,14,5,2])

运行结果：

[1, 2, 2, 2, 2, 4, 4, 4, 5, 5, 5, 8, 8, 14, 21, 24, 25, 85, 87, 87]

PS 拓展合并排序： 日后填坑
合并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
合并排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。*

首先将含有N个元素的列表拆分成两个含N/2个元素的两个子列表，在进行归并排序之前，希望这两个子列表是排好序的，就可以利用递归的思想，继续拆分并排序（最后拆分成N个子列表），然后合并两个已排好序的子列表。

对于一个含N个元素的列表，需要$log{2}^N$步把整个列表拆分成子列表，每一步至多需要比较N次，所以归并排序最多需要$N\ast log{2}^N$次比较，是一种最为常见的排序算法。

Python代码:归并递归 （日后填坑）

print("归并排序")
c=[7,9,1,0,4,3,8,2,5,4,6]
#合并两列表
def merge(a,b):#a,b是待合并的两个列表,两个列表分别都是有序的，合并后才会有序
    merged = []
    i,j=0,0
    while i<len(a) and j<len(b):
        if a[i]<=b[j]:
            merged.append(a[i])
            i+=1
        else:
            merged.append(b[j])
            j+=1
    merged.extend(a[i:])
    merged.extend(b[j:])
    return merged
#递归操作
def merge_sort(c):
    if len(c)<=1:
        return c
    mid = len(c)//2#除法取整
    a = merge_sort(c[:mid])
    b = merge_sort(c[mid:])
    return merge(a,b)

merge_sort(c)

运行结果：（返回0，说明 1 在 list 的 0 号索引）

[0, 1, 2, 3, 4, 4, 5, 6, 7, 8, 9]

3.再谈大O表示法

• 引一条经验规则：$c<log2N<n<n\ast log2N<n^2<n^3<2^n<3^n<n!$

其中c是一个常量。如果一个算法的复杂度为 $c、log2N、n、n\ast log2N$ ,那么这个算法时间效率比较高 ;
如果是 $2^n,3^n,n!$，那么稍微大一些的n就会令这个算法不能动了，居于中间的几个则差强人意。

c指的是算法所需的固定时间，被称为常量。

根据前面的经验规则可以知道，这个常量c对同样的算法复杂度影响比较大，如书中两个函数第一个c为10ms，第二个c为1s，所以前者速度快些。对于不是同一量级复杂度的，如以简单查找和二分查找作对比，c的作用影响很小。

同一算法复杂度才谈常量c;不是同一复杂度看经验表排序。
快速排序与合并排序是同一复杂度$O(n\ast logn)$,而且快速排序的常数较小，故一般情况下使用快速排序。但是在最糟糕情况下，快速排序复杂度达到了$O(n^2)$

排序算法稳定性： 快速、选择排序不稳定；合并排序稳定
所谓稳定性是指待排序的序列中有两元素相等,排序之后它们的先后顺序不变.假如为A1,A2.它们的索引分别为1,2.则排序之后A1,A2的索引仍然是1和2.

• 平均情况与最糟情况

快速排序有平均与最糟时间，性能高度依赖于你选择的基准值。

如图，每次都选取第一个元素为基准值，每次快速排序确实也分成了两个数组，其中有一个数组每次都为空。如此往复，栈的高度达到了8，也可也说选取第一个元素为基准值进行排序，总共有八层 ，最后达到基线条件完成排序。这是最糟情况，栈长为O(n)

下图这种情况，调用栈的每一层都遍历了所有元素，操作时间O(n)；总共有8层，层数又是一个n。因此最糟糕情况的时间复杂度就有了简单的表达：$O=O(n)\ast O(n)=n^2$

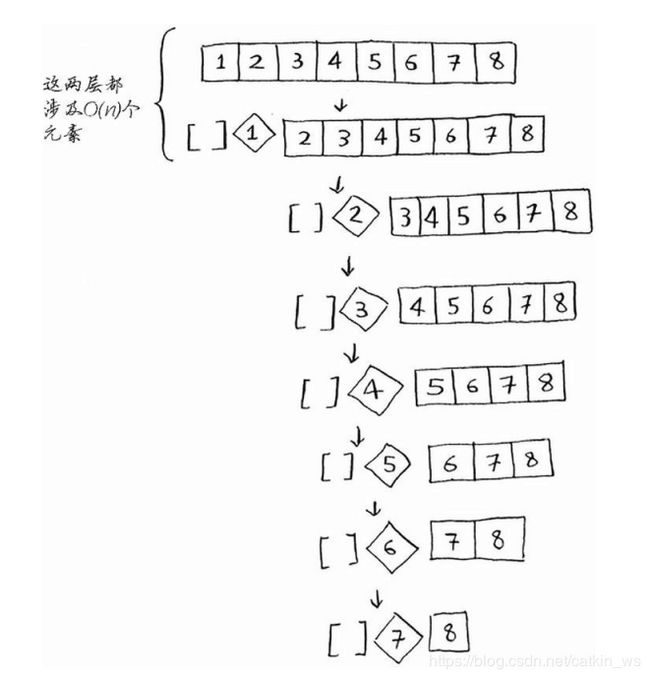
接着就是理想最优情况：

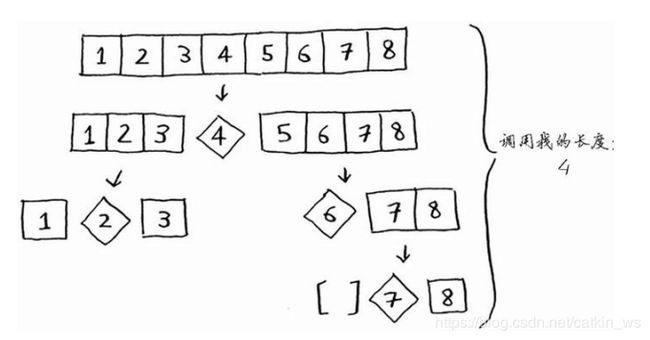
基准值每次取中间，栈的高度为4，即层数为4。调用栈少了一半，栈高O($log2n$)，而每一层他也都是遍历了所有元素，对所有元素操作时间也为O(n)。那么该平均情况时间复杂度：
$O=O(log2n)\ast O(n)=O(n\ast log2n)$

最优的时间复杂度其实也就是平均复杂度时间，当你每次随机取基准值的时候，他的复杂度也就是平均复杂度了。(最糟糕复杂度有两个特定条件：1.有序；2.取首或尾元素。其实就两种情况)

4.总结

• 1.D&C将问题逐步分解。使用D&C处理列表时，基线条件很可能是空数组或只包含一个元素的数组。
• 2.实现快速排序时，请随机地选择用作基准值的元素。快速排序的平均运行时间为O($nlogn$)。
• 3.大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因所在。
• 4.比较简单查找和二分查找时，常量几乎无关紧要，因为列表很长时，O(log n)的速度比O(n)快得多。

5.欧几里德算法

又称辗转相除法，是指用于计算两个正整数a，b的最大公约数。
python代码如下：

def gcd(a,b):
    while a != 0:
        a,b = b % a, a
    return b
gcd(40,25)

运行结果：

5

6.参考资料

《算法图解》第四章

此部分学习算法内容已上传github：https://github.com/ShuaiWang-Code/Algorithm/tree/master/Chapter4