极坐标采样实现高质量户外大气散射

原文出自GPU Pro 5 High Performance Outdoor Light Scattering Using Epipolar Sampling
原文给出的DX11 实现：https://github.com/GameTechDev/OutdoorLightScattering

翻译得比较烂，主要是给自己看的。

1、散射积分和光学厚度
在接下来的光线积分推导中，我们始终以单次散射模型作为前提，即阳光在到达相机之前只会发生一次散射
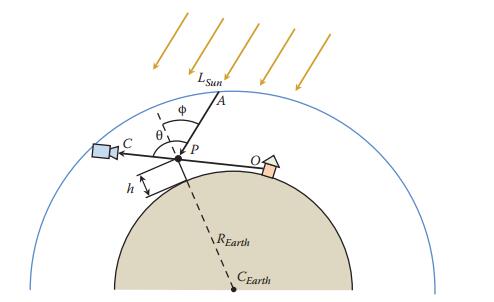
考虑如图中view ray上一点P，如果view ray不与地面相交或者相机在大气层之外，则O 或者 C就是view ray与大气层外边界的交点，衰减后达到P点的光线可表示为$L_{Sun}{e}^{-T(A\to P)}$，其中$L_{Sun}$表示阳光进入大气层之前的radiance， A则是P点对应光线进入大气层的点，$T(A\to B)$ 项表示光学厚度，本质上是光线路径上所有衰减的积分，表示为：
$$T(A\to B)={\int }_A^B({\beta }_R^e{e}^{-h(t)/H_R}+{\beta }_M^e{e}^{-h(t)/H_M})dt.$$
其中$H_R,H_M$所在项分别表示Rayleigh 和Mie 散射，两种散射与海平面的散射系数$({\beta }_{R/M}^s)$和P点的高度系数$（e^{-h/H_{R/M}})$成比例，散射至相机方向的光线比例由每种散射的相函数$p_{R/M}(\theta )$ 决定，P传播至相机的光线衰减系数为$e^{-T(P\to C)}$，最后，我们加入阴影的影响，这里由可视项$V(P)$ 决定，阴影中的位置该值为0，反之为1，最后，我们可以得出整个散射的等式：
$$L_{In}={\int }_C^O{L}_{Sun}{e}^{-T(A(s)\to P(s))}{e}^{-T(P(s)\to C)V(P(s))}({\beta }_R^e{e}^{-h(t)/H_R}{P}_R(\theta )+{\beta }_M^e{e}^{-h(t)/H_M}{P}_M(\theta ))ds$$

点O所在的物体也有光线经过衰减后达到相机，因此相机最终接受到的radiance 为：
$$L=L_O\cdot e^{-T(O\to C)}m+L_{In}$$

2、计算散射积分
上面的积分无法求出解析解，因此，我们首先消灭掉光学厚度积分$T(A\to P)$和$T(P\to C)$，光学厚度主要和海拔$h$一级光线与地表垂直方向的夹角$\phi$，因此，$T(A\to P)$可以事先预计算并存储起来，首先我们将上面的光学厚度积分重写为：
$$T(A\to B)={\beta }_R^e{\int }_A^B{e}^{-h(t)/H_R}dt+{\beta }_M^e{\int }_A^B{e}^{-h(t)/H_M}dt$$
当$B_R^e,B_M^e$为三维向量时，上式的两个积分结果都是标量，我们可以使用双通道的查找表来存储整个大气高度的Rayleigh和Mie粒子浓度，有了查找表的帮助，A到P的光学厚度可通过如下方式计算：
$$T_{A\to P}={\beta }_R^e.xyz\ast D[h,cos(\phi )].x+{\beta }_M^e.xyz\ast D[h,cos(\phi )].y$$
如果光线射到了地球，考虑到遮挡问题，对应的表格入口应当包含一个很大的数，为了避免插值导致的异常，我们在实际实现中通过允许表格中的海拔为负数来避免不连续。
计算$T(P\to C)$ 时，我们观察到从P 到 C，$\phi$的变化很小，因此我们将两个相函数作为常量提到积分外面，伪代码如下：

3、极坐标采样
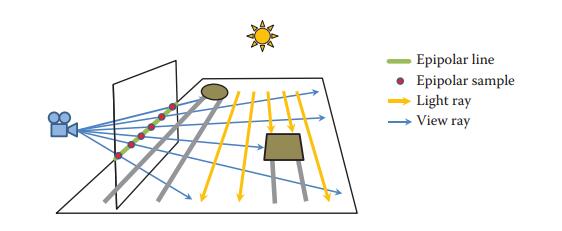
尽管上面预计算的方式计算积分已经比直接计算快了很多，但每个像素都进行上述操作还是过于昂贵。而如果采用极坐标采样的话，计算量将戏剧性的减少，极坐标采样很聪明的将昂贵的raymarching 沿极线分布在屏幕上。通过连接光源在屏幕的投影位置和屏幕边缘用户定义数量的等距的点获得极线。注意边缘坐标系应依据最远的像素中心来建立，即偏移0.5个像素大小。在投影空间，定义如下矩形：[-1 + 1/W, 1 - 1/W] x [-1 + 1/H, 1 - 1/H]，W和H是屏幕的宽高。
如果光源在屏幕范围内，每条极线的起点就是光源的屏幕位置，反之，则起点在极线与屏幕边界的交点，如下图所示：

与屏幕没有交点的极线将在后面的步骤中被抛弃。然后，预先定义好数量的采样点均匀的分布到极线的起点和重点之间，每隔N个采样点选一个作为初始化的raymarching 采样点，起点和终点则总是算作采样点，为了反之较短的极线上做过度的采样，我们延长这样的线，尽量让采样点和像素达到1：1的比例。
[Engelhardt and Dachsbacher 10]对该算法提出了优化，即搜索屏幕中深度不连续的部分，但我们发现那不是一个好的策略因为我们需要的是关照强度不连续的部分。在我们的方法中，我们首先对每个采样点做粗糙的计算未被阴影覆盖的in-scattering（V = 1）， 为此，我们使用了梯形积分，我们存储上一个点的粒子浓度并更新从相机到当前点的总体浓度：

Rayleigh 和 Mie 散射通过如下方式更新：

4、1D min/max 二叉树优化
现在我们在每条极线上选择一定数量的采样点并计算考虑了阴影的in-scattering，对每一个采样点，我们发射一条射线，并将其起点终点映射到灯光投影空间然后在shadowmap空间进行raymarching 操作。

遍历shadowmap的每个纹素过于昂贵，尤其对于高分辨率的shadowmap，使用固定数量的采样点则会导致采样不足并导致banding antifact。我们通过使用极坐标几何体来提高性能同时不牺牲视觉效果，如下图所示，考虑同一条极线上采样点所发射的view ray，其显然是落在同一个平面上的，我们称该平面为极平面，其最重要的属性是光线向量也都落在该平面上。

该平面上的所有view ray起点都在极线上，只有终点不一样，沿view ray采样shadowmap 则可以得到一个一维的高度图，且该极平面上的所有view ray 采样得到的高度图是一样的。

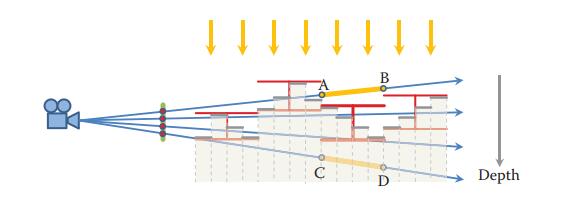
为了进行可视性测试 $V(P)$ ，本质上来说我们需要确定当前采样点在showmap采样的高度图之上还是之下，如下图所示：

显然如果我们知道有一段很长的连续阴影或者非阴影，我们就能立即处理它而不需要遍历路径上所有的采样点，为了实现这个目标，[Chen et al. 11]建议使用一个一维的 min/max 二叉树，与他不同的是，我们没有对shadowmap进行矫正，这使得我们的算法要简单得多。如果view ray上某一节最大深度小于二叉树对应节点中的最小深度值，那么这一段就肯定是没有阴影的，如上图中的AB，反之，则如果最小值大于二叉树结点的最大值，那么这一段就都在阴影中，如图中CD

5、构建二叉树
为了针对该极平面构建二叉树，我们需要定义极平面与shadowmap的交线，因为所有的view ray都要投影到该交线上，这里可以通过取射线上的两个不同点并映射到shadow map uv空间。在我们的实现中，我们使用相机位置作为第一个点。它的投影位置 $O_{UV}$ 给了我们第一个高度图采样点。为了计算其方向 $D_{UV}$，我们取射线在极平面的终点，映射到 UV 空间并计算方向。然后我们归一化$D_{UV}$。如果$O_{UV}$落在了shadowmap范围之外（即UV坐标不在0到1之间），我们沿 $D_{UV}$延长，并将$O_{UV}$设置到延长线与[0,1]区域的第一个交点，如下图所示：

现在我们知道了第0个1D高度图上的采样点$O_{UV}$和方向$D_{UV}$，那么第 i 个采样就是 $O_{UV}+i\cdot D_{UV}$，计算第 2i 个和 2i + 1 个采样点的 min/max 就能得到二叉树的第一层。同理可以构建出整棵二叉树，在上图中可以看到，采样点并不是准确的落在shadowmap的纹素中心，为了取得正确的结果，我们取最近的四个纹素并计算 min/max

6、基于1D min/max 二叉树的 Raymarching
我们优化后的raymarching算法建议自[Tevs et al. 08]， min/max 二叉树遍历在无需递归的情况下进行，通过将采样序号除以 $2^{l+1}$从 $l$ 层到 $l+1$层，直到该节点下的所有采用点都统一处于阴影或者非阴影状态下。该算法保持追踪当前的 min/max 层，根据需要增加或者减少层。当in-scattering 积分更新时，当前节点长度 $ds$ 缩放 $2^l$ 倍，后面的章节将给出 shader 代码

严格来说，计算长度为 $2^l$ 的采样片段的散射贡献和逐点计算所有采样点的积分结果并不相同，因为积分不是线性的。对于一个点光源，我们通过预计算散射积分并存储到2D查找表来解决，但户外光源需要预计算4D查找表 [Bruneton and Neyret 08]，这使得每次查找都很昂贵，因为查找表的参数是非线性的。幸运的是，积分函数变化得很缓慢，即使是阶梯积分也能取得大致准确的结果。

7、算法步骤

1、渲染相机的深度图 tex2DSliceEndPoints

2、计算每条极线终点的屏幕空间坐标，然后将其渲染到一个 $N_{Slices}\times 1$ 的贴图 tex2DSliceEndPoints 中

3、渲染$N_{Samples}\times N_{Slices},RG32F$ xy坐标贴图 tex2DCoordinates（第 i 行第 j 个纹素的 rg 值表示 第 j 个极平面上 第 i 个采样点的屏幕空间坐标， 同时也是在这一步读取tex2DSliceEndPoints 并discard掉不可见的极线） ，相机空间极坐标 z 的 $N_{Samples}\times N_{Slices},R32F$贴图 tex2DEpipolarCamSpaceZ，并设置$N_{Samples}\times N_{Slices}$ 的stencil 缓存 tex2DEpipolarStencil
(a)、极线上的每个采样点的屏幕坐标通过该线的终点插值得到
(b)、为了计算采样点的相机深度，采样点深度图需要线性过滤
©、模板缓存是为了标记在屏幕内的采样点

4、对于每一个可用的采样点，通过第四节提供的方法粗糙的计算其散射积分并存储在贴图 tex2DInitialInsctr 中($N_{Samples}\times N_{Slices},RGB16F$)
(a)、tex2DEpipolarStencil 是为了剔除屏幕外的采样点
(b)、$N_{Steps}=7$的梯形积分提供了性能和准确性之间一个很好的平衡
©、这里我们还要渲染衰减贴图 tex2DEpipolarExtinction $N_{Samples}\times N_{Slices}，RGBA8U$，用来衰减背景颜色

5、tex2DInitialInsctr 中的积分结果用来改善采样和插值计算的源贴图
tex2DInterpolationSource $N_{Samples}\times N_{Slices}，RG16U$

6、确定极平面的原点和方向，并存储到 tex2DSliceUVDirAndOrigin $N_{Slices}\times N_{Cascades}，RGBA32F$

7、构建 min/max 二叉树并存储到 tex2DMinMaxDepth $S{M}_{Dim}\times (N_{Slices}\cdot N_{Cascades}),RG16U$
(a)、tex2DSliceUVDirAndOrigin 用来取第 0 个采样点和其方向，计算当前需要的采样点的位置，构建出叶子节点
(b)、构建其余根节点

8、使用插值源贴图 tex2DInterpolationSource 来更新模板缓存 tex2DEpipolarStencil 并标记将要进行raymarching采样的采样点，对于这些采样点，插值源是一样的

9、对所有标记的采样点进行 raymarching 操作，散射结果渲染到 tex2DInitialInsctr （之前存储粗糙结果现在拿来重用）

10、初始散射结果 tex2DInitialInsctr 通过 tex2DInterpolationSource 在所有采样点间进行插值，结果存储到 tex2DEpipolarInscattering

11、最后，将 tex2DEpipolarInscattering 的结果映射到屏幕空间并叠加到衰减后的背景缓存

较为重要的步骤细节将在后面的章节讲到

8、采样优化
采样优化的步骤尝试了插值源贴图 tex2DInterpolationSource， 其存储了同一条线上的两个采样点。这一步通过 compute shader实现，并包含了两步。第一步，如果tex2DInitialInsctr 中相邻的两个采样点的粗糙散射结果有较大的不同则用1 bit的标记填充一个全局数组，标记值通过如下方式计算：

该标记通过 InterlockedOr() 打包为 32位的 unit

第二步，通过 firstbitlow() 和 firstbitlow() 标记出用来插值的采样点，这个两个函数分别返回从第一个和最后一个位置开始的非零的bit位位置

9、二叉树构建实现
我们将二叉树存储为 $S{M}_{Dim}\times (N_{Slices}\cdot N_{Cascades}),RG16U$， 其包含了所有shader cascade中的所有极平面的所有树，每一个1D高度图包含了多余 $S{M}_{Dim}$ 个的采样点，所以，存储高度图本身是没有必要的，二叉树所有根节点层级被打包进 $S{M}_{Dim}-1$ 个采样点 。这样第一级开始于 x = 0 列，第二级开始于 x = $S{M}_{Dim}/2$ 列，以此类推，第 i 个 cascade 开始于 y = $N_{Slices}\cdot i$ 行

前三个层级通过从 tex2DSliceUVDirAndOrigin 中读取极平面原点 $O_{UV}$ 和方向 $D_{UV}$ ，通过 $O+UV+2i\cdot D_{UV},O+UV+(2i+1)\cdot D_{UV})$ 计算当前需要的两个采样点在shadowmap上对应的位置和 min/max 深度。为了获取连续的边界，对每个采样点我们使用 Gather() 指令同时采样4个位置的深度。我们使用 16位的贴图来节省内存和带宽，因为从32位转换到16位会损失精度，因此我们需要小心处理：

二叉树的父节点通过读取两个子节点的 min/max 值来构建，为了实现这个，我们使用两张贴图，分别设置为源和目标。因为实际运行中不太可能会遍历二叉树中所有层级，我们限制树的高度为 shadowmap分辨率的 1/16。

10、Raymarching Shader
将 tex2DInitialInsctr 设置为当前渲染目标， 使用 tex2DEpipolartex2DEpipolar 来保证shader只针对标记过的采样点运行。（代码概要见原文，完整代码见github）

11、展开
算法的最后一步将插值后的radiance存储在 ptex2DEpipolarInscattering 贴图从极坐标空间转换到屏幕空间。我们通过找两个最近的极线并将采样点投影上去，然后我们使用 Gather() 指令去从 tex2DEpipolarCamSpaceZ 取两条线上最近的两个点相机深度并通过比较两者的屏幕 z 坐标（从 tex2DCamSpaceZ 取得）计算双边权重。通过双边权重，我们通过 Sample() 指令调整过滤位置来获取每条极线的in-scattering的权重和。最后，我们将in-scattering值和衰减后的背景缓存合并