Tensorflow实战：深层神经网络

深层神经网络

Wiki上对深度学习的定义为“一类通过多层非线性变换对高复杂性数据建模算法的合集”。深度学习有两个非常重要的特性—多层和非线性

去线性化

因为线性模型只能解决线性可分的问题，针对较多的线性不可能问题，需要对模型去线性化。这里引入了激活函数,激活函数可以实现去线性化。普通的神经元的输出通过一个非线性函数，整个神经网络的模型由线性转为非线性了.

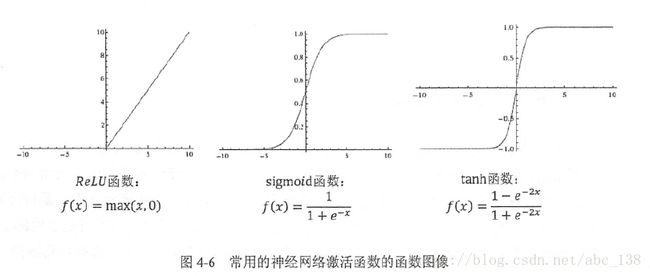
常用的激活函数有:

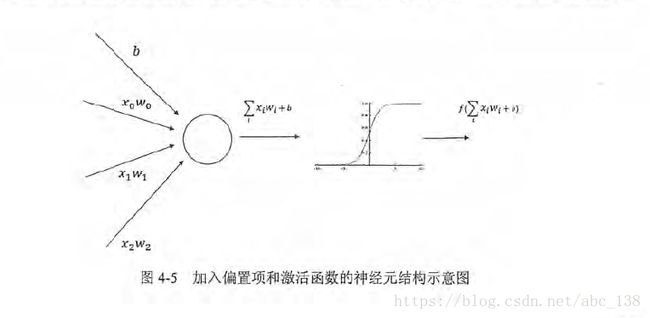
针对上面讲的神经网络，这里我们加入偏置项和激活函数的神经网络结构如下:

 

 

 

 

多层

多层神经网络有组合特征提取的功能，这个特性对解决不易提取特征向量的问题有很大帮助.这也是深度学习在多种问题上突破的原因.

损失函数

神经网络模型的效果以及优化目标是通过损失函数(loss function)来定义的.

经典损失函数

分类问题和回归问题是监督学习的两大种类。在分类问题上，通过神经网络解决分类问题常用的方法是设置n个输出节点，n为类别的个数。这时候需要判断输出指标，该如何确定一个输出向量和期望的向量有多接近。这里我们使用了交叉熵损失函数。

交叉熵

交叉熵(cross entropy)是分类问题常用的评判方法之一.

熵 熵的本质是香农信息量的期望。

 

 

分类问题-交叉熵

交叉熵刻画的是通过两个概率分布的距离，即通过概率分布q表达概率分布p的困难程度

 

 

 给出一个具体的样例直观的说明交叉熵可以判断预测与标签值之间的距离:

TensorFlow中的交叉熵实现

我们实现的交叉熵代码如下:

cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y,1e-10,1.0)))
其中y_代表标签值，y代表预测值。

 先说tf.clip_by_value函数，该函数可以将一个张量的值限制在一个范围内

    v = tf.constant([[1.0,2.0,3.0],[4.0,5.0,6.0]])
    print tf.clip_by_value(v,2.5,4.5).eval()
    #v中小于2.5的转换为2.5 大约4.5的转换为4.5

    tf.clip_by_value(y,1e-10,1.0)
    #保证下一步的log值不会错误

tf.log 即完成对张量中所有元素的依次求对数功能

    v = tf.constant([1.0,2.0,3.0])
    print tf.log(v).eval()
    #输出[ 0.        ,  0.69314718,  1.09861231]

    tf.log(tf.clip_by_value(y, 1e-10, 1.0))
    #对输出值y取对数

乘法 在实现交叉熵代码中直接将两个矩阵通过*操作，代表是元素之间相乘(矩阵乘法使用的是tf.matmul函数)

    v1 = tf.constant([[1.0,2.0],[3.0,4.0]])
    v2 = tf.constant([[5.0,6.0],[7.0,8.0]])
    print (v1*v2).eval()
    #输出[[  5.  12.]  [ 21.  32.]]

    print tf.matmul(v1,v2).eval()
    #输出[[ 19.  22.] [ 43.  50.]]

    y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))
    #完成了对于每一个样例中的每一个类别交叉熵p(x)logq(x)的计算.
    #得到一个n × m的矩阵,n为一个batch数量，m为分类类别的数量。

取平均值 根据交叉熵公式，应该将每行中m个结果相加得到所有样例的交叉熵，再对n行取平均得到一个batch的平均交叉熵.因为分类问题的类别数量不变，可以直接对整个矩阵平均.

    v = tf.constant([[1.0,2.0,3.0],[4.0,5.0,6.0]])
    print tf.reduce_mean(v).eval()
    #平均输出为3.5

    -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0)))

因为交叉熵一般会与Softmax回归一起使用,所以TensorFlow对这两个功能统一封装，并提供
tf.nn.softmax_cross_entropy_with_logits函数.使用下面程序实现softmax回归后的交叉熵损失函数:

cross_entropy = tf.nn.softmax_cross_entropy_with_logits(y,y_)

在只有一个正确答案的分类问题中，TensorFlow提供了tf.nn.sparse_softmax_cross_entropy_with_logits()函数进一步加速计算过程。

回归问题-均方误差(MSE,mean squared error)

回归问题解决的是对具体数值的预测，需要预测的不是一个事先定义好的类别，而是一个任意实数。解决回归问题的神经网络一般只有一个输出节点，这个节点的输出值就是预测值.

自定义损失函数

TensorFlow支持自定义损失函数。例如

loss = tf.reduce_sum(tf.select(tf.greater(v1,v2),(v1-v2)*a,(v2-v1)*b))

在此段代码中用了两个函数

• 比较函数 tf.greater(v1,v2)
  tf.greater(v1,v2)的输入是两个张量，函数会比较两个张量每一个元素的大小，返回操作结果

• 选择条件函数 tf.select(select不可用，暂时不知道原因)
  tf.select有三个参数，第一个是选择条件的根据(类似?:操作符)，如果为True则选中第二个参数.否则选中第三个参数

#  coding:utf8
import tensorflow as tf

v1 = tf.constant([1.0, 2.0, 3.0, 4.0])
v2 = tf.constant([4.0, 3.0, 2.0, 1.0])

with tf.Session() as sess:
    print(sess.run(tf.greater(v1, v2)))
    print(sess.run(tf.where(tf.greater(v1, v2), v1, v2))) 
    #select不可用，使用where代替

输出:
[False False  True  True]
[4.0 3.0 3.0 4.0]

 使用自定义函数的完整历程代码:

    import tensorflow as tf

    #使用NumPy工具包生成模拟数据集
    from numpy.random import RandomState

    #定义训练数据batch大小
    batch_size = 8


    #输出一般只有一个输出节点
    x = tf.placeholder(tf.float32, shape=(None, 2), name='x-input')
    y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y-input')

    #定义一个单层神经网络前向传播过程,这里就是简单的加权和
    w1 = tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
    y = tf.matmul(x, w1)


    #定义预测成本
    loss_less = 10
    loss_more = 1
    loss = tf.reduce_sum(tf.where(tf.greater(y,y_),(y-y_)*loss_more,(y_-y)*loss_less))

    # 定义学习率
    learning_rate = 0.001

    # 定义BP算法优化神经网络参数
    train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss)

    #通过随机数生成一个数据集
    rdm = RandomState(1)
    dataset_size = 128
    X = rdm.rand(dataset_size,2)

    #设置回归的正确值为两个输入的和加上一个噪声值。
    Y = [[x1+x2+rdm.rand()/10.0-0.05] for (x1,x2) in X]

    #创建会话运行程序
    with tf.Session() as sess:
        sess.run(tf.initialize_all_variables())

        STEPS = 5000
        for i in range(STEPS):
            #每次选取batch_size个样本训练
            start = (i*batch_size) % dataset_size
            end = min(start+batch_size,dataset_size)
            sess.run(train_step,feed_dict={x:X[start:end], y_:Y[start:end]})
        print(sess.run(w1))

神经网络优化算法

本节更加具体的介绍如何通过BP算法和梯度下降法调整神经网络的参数。梯度下降法主要用于优化单个参数的取值，而BP算法给出了一个高效的方式在所有参数上使用梯度下降法，从而使神经网络在训练数据上损失函数尽可能的小.

需要注意的是，梯度下降法并不能保证被优化的函数达到全局最优解。
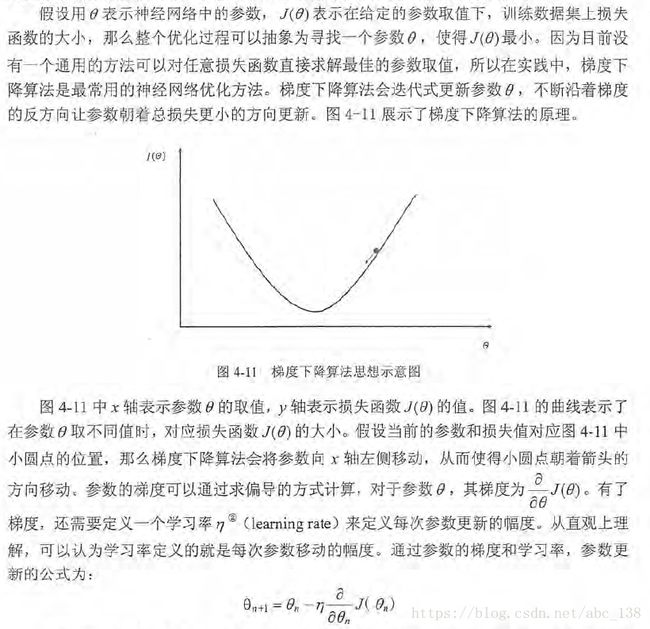
图示，优化点陷入局部最优解，而不是全局最优。可见在训练神经网络时，参数的初始值会很大程度影响最后得到的结果.

梯度下降法的计算时间太长。因为要在全部的训练数据上最小化损失，所以损失函数J(θ)是所有训练数据的损失和。在海量数据下，计算全部训练数据上的损失函数是非常耗时的。

为了加速训练过程，可以使用随机梯度下降法(stochastic gradient descent)。这个算法是在每一轮迭代中，随机优化某一条训练数据上的损失函数。这样速度就大大加快了。同时这方法的问题也很明显:使用随机梯度下降法可能连局部最优也达不到。

这里采用折中的办法:每次计算一小部分训练数据的损失函数(即一个batch)，通过矩阵运算。每次一个batch上优化神经网络参数速度并不会太慢，这样收敛速度得到的保证，收敛结果也接近梯度下降的效果。

下面代码给出了TensorFlow中如何实现神经网络的大致训练过程:

#定义训练数据batch大小
    batch_size = n


    #每次读取一小部分
    x = tf.placeholder(tf.float32,shape=(batch_size,2),name='x-input')
    y_ = tf.placeholder(tf.float32,shape=(batch_size,1),name='y-input')


    #定义神经网络结构和优化算法
    loss =...

    # 定义学习率
    learning_rate = 0.001

    # 定义BP算法优化神经网络参数
    train_step = tf.train.AdamOptimizer(learning_rate).minimize(loss)

    #训练网络
    with tf.Session() as sess:
        #参数初始化等
        sess.run(tf.initialize_all_variables())

        #迭代更新参数
        STEPS = 5000
        for i in range(STEPS):
            #每次选取batch_size个样本训练,一般将所有训练数据打乱后选取
            current_X,current_Y = ...
            sess.run(train_step,feed_dict={x:X[start:end], y_:Y[start:end]})

学习率的设置

学习率决定参数每次更新的幅度，如果幅度过大，可能导致参数在最优值两侧来回移动。如果幅度过小，会大大降低优化速度。为了解决这个问题，TensorFlow提供了一种更加灵活的学习率设置方法–指数衰减法。使用以下函数

tf.train.exponential_decay(
    learning_rate,
    global_step,
    decay_steps,
    decay_rate,
    staircase=False,
    name=None
)

参数含义:

• learning_rate: A scalar float32 or float64 Tensor or a Python number. The initial learning rate.(初始学习率)
• global_step: A scalar int32 or int64 Tensor or a Python number. Global step to use for the decay computation. Must not be negative.
• decay_steps: A scalar int32 or int64 Tensor or a Python number. Must be positive. See the decay computation above.(衰减速度)
• decay_rate: A scalar float32 or float64 Tensor or a Python number. The decay rate.(衰减系数)
• staircase: Boolean. If True decay the learning rate at discrete intervals
• name: String. Optional name of the operation. Defaults to ‘ExponentialDecay’.

函数功能:
The function returns the decayed learning rate. It is computed as:

decayed_learning_rate = learning_rate *
                    decay_rate ^ (global_step / decay_steps)

如果参数staircase为True，global_step / decay_steps 结果会取整，此时学习率成为阶梯函数(staircase function).
下图连续的学习率曲线是staircase为False，阶梯曲线是staircase为True.

 

应用示例:
Example: decay every 100000 steps with a base of 0.96:

global_step = tf.Variable(0, trainable=False)
    starter_learning_rate = 0.1
    learning_rate = tf.train.exponential_decay(starter_learning_rate, global_step,
                                               100000, 0.96, staircase=True)
    # Passing global_step to minimize() will increment it at each step.
    learning_step = (
        tf.train.GradientDescentOptimizer(learning_rate)
        .minimize(...my loss..., global_step=global_step)

过拟合问题

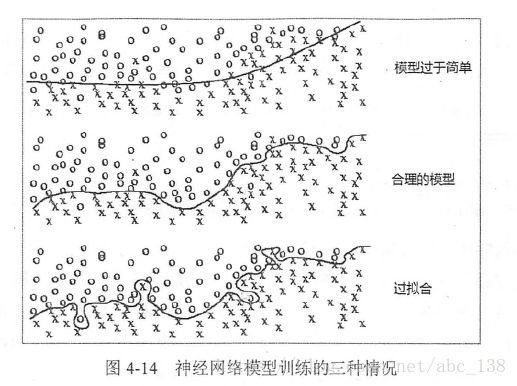
过度拟合训练数据中的随机噪声虽然可以得到非常小的损失函数，但是对未知数据可能无法做出可靠的判断.如下图

 

使用TensorFlow可以优化任意形式的损失函数，以下代码给出了一个简单的带L2正则化的损失函数定义:

#tensorflow.contrib.layers模块需要导入
    import  tensorflow.contrib.layers as tflayers

    w = tf.Variable(tf.random_normal([2,1],stddev=1,seed=1))
    y = tf.matmul(x,w)

    loss = tf.reduce_mean(tf.square(y_ - y)) +                    tflayers.l2_regularizer(lambda)(w)  
    #lambda为正则化权重  实际过程中lambda为关键字

 

loss定义为损失函数，由两个部分组成，第一个部分是均方误差损失函数，刻画模型在训练数据上的表现。第二部分就是正则化，防止模型过度模拟训练数据中的随机噪声.

类似的,tensorflow.contrib.layers.l1_regularizer可以计算L1正则化的值。

在简单的神经网络中，上述代码可以很好地计算带正则化的损失函数，但当神经网络的参数增多之后，这样的方式可能导致loss函数定义可读性变差，更主要的是导致，网络结构复杂之后定义网络结构的部分和计算损失函数的部分可能不在同一函数中，这样通过变量这样方式计算损失函数就不方便了.

以下代码使用TensorFlow中给提供的集合(Collection)解决一个5层神经网络带L2正则化的损失函数计算方法:

    # tensorflow中集合的运用:损失集合
    # 计算一个5层神经网络带L2正则化的损失函数
    import tensorflow as tf
    import  tensorflow.contrib.layers as tflayers
    from numpy.random import RandomState

    #获得一层神经网络边上的权重，并将这个权重的L2 正则化损失加入名称为'losses'的集合里
    def get_weight(shape, lamada):
        # 生成对应一层的权重变量
        var = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
        tf.add_to_collection('losses', tflayers.l2_regularizer(lamada)(var))
        return var

    x = tf.placeholder(tf.float32, shape=(None, 2), name='x_input')
    y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y_input')

    batch_size = 8

    # 定义每层神经网络的节点个数
    layer_dimension = [2, 10, 10, 10, 1]
    # 获取神经网络的层数
    n_layers = len(layer_dimension)
    # 这个变量表示前向传播时最深层的节点，最开始的时候是输入层
    cur_layer = x
    # 当前层的节点个数
    in_dimension = layer_dimension[0]

    # 通过一个循环生成5层全连接的神经网络结构
    for i in range(1, n_layers):
        # 获取下一层节点的个数
        out_dimension = layer_dimension[i]
        # 获取当前计算层的权重并加入了l2正则化损失
        weight = get_weight([in_dimension, out_dimension], 0.001)
        # 随机生成偏向
        bias = tf.Variable(tf.constant(0.1, shape=[out_dimension]))
        # 计算前向传播节点，使用RELU激活函数
        cur_layer = tf.nn.relu(tf.matmul(cur_layer, weight) + bias)
        # 进入下一层之前，更新下一层节点的输入节点数
        in_dimension = layer_dimension[i]

    # 计算模型数据的均值化损失加入损失集合
    mse_loss = tf.reduce_mean(tf.square(y_ - cur_layer))
    tf.add_to_collection('losses', mse_loss)

    # get_collection返回一个列表，列表是所有这个集合的所有元素
    # 在本例中，元素代表了其他的损失，加起来就得到了所有的损失
    loss = tf.add_n(tf.get_collection('losses'))

    global_step = tf.Variable(0)
    # 学习率的设置：指数衰减法，参数：初始参数，全局步骤，每训练100轮乘以衰减速度0,96(当staircase=True的时候)
    learning_rate = tf.train.exponential_decay(0.1, global_step, 100, 0.96, staircase=True)
    train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)

    rdm = RandomState(1)
    dataset_size = 128
    X = rdm.rand(dataset_size, 2)
    # 加入了一个噪音值，-0.05～0.05之间
    Y = [[x1 + x2 + rdm.rand() / 10.0 - 0.05] for (x1, x2) in X]

    with tf.Session() as sess:
        init_op = tf.initialize_all_variables()
        sess.run(init_op)
        # print sess.run(w1)

        steps = 5000
        for i in range(steps):
            start = (i * batch_size) % dataset_size
            end = min(start + batch_size, dataset_size)

            sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
            if i % 1000 == 0:
                total_loss = sess.run(
                    loss, feed_dict={x: X, y_: Y})
                print("After %d training_step(s) ,loss on all data is %g" % (i, total_loss))
                # print sess.run(w1)

滑动平均模型

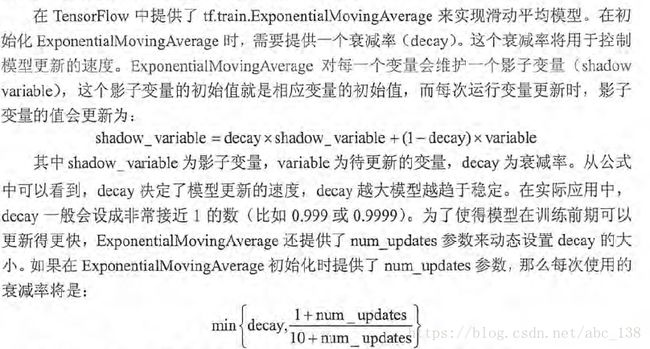
在采用随机梯度下降算法训练神经网络时，使用滑动平均算法模型可以提供模型的鲁棒性(robust).TensorFlow中提供了tf.train.ExponentialMovingAverage来实现滑动平均模型.

    #滑动平均模型的小程序
    #滑动平均模型可以使得模型在测试数据上更加健壮
    import tensorflow as tf

    #定义一个变量用以计算滑动平均，变量的初始值为0,手动指定类型为float32，
    #因为所有需要计算滑动平均的变量必须是实数型
    v1 = tf.Variable(0,dtype=tf.float32)

    #模拟神经网络迭代的轮数，动态控制衰减率
    step = tf.Variable(0,trainable=False)
    #定义一个滑动平均的类，初始化时给定衰减率为0.99和控制衰减率的变量
    ema = tf.train.ExponentialMovingAverage(0.99,step)

    #定义一个滑动平均的操作，这里需要给定一个列表，每次执行这个操作时，列表里的元素都会被更新
    maintain_average_op = ema.apply([v1])

    with tf.Session() as sess:
        #初始化所有变量
        init_op = tf.initialize_all_variables()
        sess.run(init_op)

        #获取滑动平均之后变量的取值
        print sess.run([v1,ema.average(v1)])

        #更新v1的值为5
        sess.run(tf.assign(v1,5))
        #更新v1的滑动平均值，衰减率为min{0.99,(1+step)/(10+step)=0.1}=0.1,
        #所以v1的滑动平均被更新为0.1*0+0.9*5=4.5
        sess.run(maintain_average_op)
        print sess.run([v1,ema.average(v1)])

        #更新迭代的轮数
        sess.run(tf.assign(step,10000))
        sess.run(tf.assign(v1,10))
        #这里的衰减率变成0.99
        #v1 = 0.99*4.5+0.01*10=4.555
        sess.run(maintain_average_op)
        print sess.run([v1,ema.average(v1)])

        #再次更新滑动平均值
        sess.run(maintain_average_op)
        print sess.run([v1,ema.average(v1)])