算法练习 - 最长回文字串(Manacher 算法学习)
题目描述
给定一个字符串,求它的最长回文子串的长度。
Manacher算法
这是一个经典的算法问题,近期在网上看了很多人的讲解,感觉仍不是特别清晰,起码看起来还是有些累的。终于在看了一个英文介绍(http://articles.leetcode.com/2011/11/longest-palindromic-substring-part-ii.html),又苦苦思索1天后,豁然开朗,所以把自己的学习心得记录下来,以方便以后复习。
首先放上C++的程序实现(代码引自http://articles.leetcode.com/2011/11/longest-palindromic-substring-part-ii.html,添加了一些注释,将结尾查找起始点的部分删除),代码十分晦涩,如果不需要知道原理只需要实现方法的朋友,请直接粘贴到你的程序中即可运行。如果希望知道原理,请结合后面的分析阅读。
/**********************************************************
* Manacher's algorithm should insert special character(#)
* into original string, then all strings whatever it's
* length is odd or even will be extened to even.
* And add a specila charactor at the begin and end of the
* string to avoid over position limitition. Such as
* "abaca" should be change to "^#a#b#a#c#a#$"
**********************************************************/
string ManacherPreprocess(const string& str)
{
string s = "^";
for(string::size_type i = 0; i < str.length(); ++i)
{
s+="#";
s+=str[i];
}
s+="#$";
return s;
}
/**********************************************************
* find out the longest palindromic substring.
**********************************************************/
string LongestPalindromeManacher(const string& str)
{
string T = ManacherPreprocess(str);
int cIndex = 0; //index of center of Palindromic substring in T. the substring is the nearest and longest
int rightEdge = 0; //right edge index of Palindromic string centers at cIndex.
// store intermediate result in an array P,
// where P[i] equals to the length of the palindrome centers at T[i].
int N = T.length();
int *P = new int[N];
//Length of the longest Palindromic substring
int maxLen = 0;
int centerIndexOfMax = 0;
for(int i = 1; i < N - 1; ++i)
{
//mirrorIndex is the mirrored index of i based on cIndex.
//In fact, this mirrorIndex is only meaningful while i is
//in the index range of Palindromic string which center is cIndex.
//
//If i is out of range, should calculate Palindromic string
//centered in i.
int mirrorIndex = 2 * cIndex - i;
//We assume there's a Palindromic string which centers at cIndex.
P[i] = (rightEdge > i) ? min(rightEdge-i, P[mirrorIndex]) : 0;
//Try to find out the Palindromic string which center is i
while(T[i + 1 + P[i]] == T[i - 1 - P[i]])
P[i]++;
if((i + P[i]) > rightEdge)
{
//Palindromic string centers at cIndex even cannot cover T[i],
//so cannot conver the right parts. so move cIndex to i and update rightEdge.
cIndex = i;
rightEdge = i + P[i];
}
//Record index of which item in P contains the longest Palindromic substring
//and the length of the substring.
//These will be used to find out the real substring from input str.
if(maxLen < P[i])
{
maxLen = P[i];
centerIndexOfMax = i;
}
}
/* Original statements which cost extra O(N), so remove */
/* Find the maximum element in P.
/***********************************************************/
//int maxLen = 0;
//int centerIndexOfMax = 0;
//for (int i = 1; i < N-1; i++)
//{
// if (P[i] > maxLen)
// {
// maxLen = P[i];
// centerIndex = i;
// }
//}
delete []P;
return str.substr((centerIndexOfMax - 1 - maxLen)/2, maxLen);
}如果一个字符串从第1位开始读到最后1位与从最后1位开始读到第1位的结果是一样的,那么这个字符串就是回文字符串。如:“aba”,“ababa”是回文字符串,但是“abc”,“abca”就不是回文字符串。
算法分析
对于任何一个算法问题,我们都可以找到一个最原始、最简单(想起来简单),但是效率(从时间复杂度和空间复杂度考量)可能一般或者很差的方法,而这些方法中,穷举法几乎又是解决一切问题的万能汤药(虽然大部分时候效率低到没朋友)。
穷举法带来的思考
对于本题目,使用穷举法就是以字符串中每一个字符为中心,查找其对应的回文字符串,然后在所有找到的字符串中找出最长的那个。比如字符串abcb,就可以找到以c为中心点的回文子串bcb。不过即使这样做,仍然有一个问题,比如字符串abccb,它的回文子串是cc,因为bccb是4位,所以bccb的中心点没有字符,或者说bccb的中心点是2个字符cc。
到这里我们不难发现,回文字符串有2种,偶数位长度和奇数位长度。因此写代码实现的时候也要分为2中情况考虑。从而增加了时间复杂度。穷举法因为实现起来相对简单,这里暂时不做进一步的讨论和实现。
Manacher 算法
Manacher算法首先解决的就是回文字符串长度有奇数有偶数的问题。其做法就是在字符串的每个字母之间以及首字符的前面和最后一个字符的后面分别添加一个新的字符“#”,从而使所有的字符串都变成奇数长度。比如:”aba“经过处理后变为“#a#b#a#”,“abac”处理后变为“#a#b#a#c#”。
现在简单说明一下原理,如果一个字符串长度为n,那么按照前述规则可以插入的字符“#”的个数为n-1+2,即n+1个,从而长度为n的字符串处理后的长度就变为n+n+1=2n+1,因此不论原字符串长度是奇数还是偶数,变更后的字符串的长度都将是奇数,而且因为对于任何一个字符来说“#”都是对称添加的,回文字符串添加“#”后,仍然是回文字符串。比如:字符串“aba”,添加“#”后变为#a#b#a#“,仍然是回文字符串。
这样一来,所有的字符串就都可以被统一处理了。处理的方法仍然是依次查找以每个字符为中心的回文字符串,并将该回文字符串的长度记录到一个与处理后的字符串等长的整数数组的对应位置上。(这里假设回文字符串长度不会超过整形数据最大值,超长的极端情况这里暂时不作讨论)
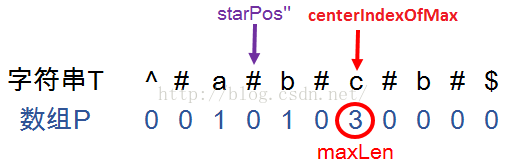
现在以下面的字符串为例进行说明
数组P中保存的是以字符串T中对应位置的字符为中心的回文字符串的1/2长度(注意,这里的1/2指的是计算机中的整数除法,即向下取整,如4/2=2,5/2=2)。比如P[3] = 3,表示T中以a(T[3]位置)为中心点的回文字符串是”#b#a#b#“,长度为7,除以2后即为3。其实对照原字符串S,可以发现,“#b#a#b#”去除”#“后的字符串”bab“正是字符串S以S[2]的a为中心的回文字符串,而且”bab“的长度正好也是3。这是巧合吗?当然不是!!!
还记得前面添加“#”的时候做的计算吗?任意一个字符串S,变为T要添加n+1个字符串,从而使长度变为2n+1,所以1/2T中回文字符串的长度正好等于该字符串还原成S后的长度((2n+1)/2)。因此在计算P[i]的时候,根本就是以T[i]为中心点,数了一半的长度(毕竟回文字符串是照镜子似的对称的 :P),可以参考代码的55,56行
对于任意字符串,在查找以其中一个字符为中心的回文子字符串的时候,可能会有下面几种情况,现在仍然以上面的字符串为例,逐一进行讨论。
情况一:在T[i]之前,字符串T中没有任何一个子回文字符串
如图所示,T[1](画红圈的b)之前,只有一个字符”#“,没有回文字符串
此时计算P[i]非常简单,即以i所在位置的字符为中心,向两边查找,P[i]的初始值是0,然后找到一对相等的字符,P[i]就加1,直到遇到不相等的字符对为止。上例就是以b为中心,找到一对相同的字符对“#”,因此P[1]为1。代码表达如下(这里i从1开始):
P[i]=0;
int left = i;
int right = i;
while(T[right++] == T[left--])
P[i]++;在这段代码中,引入了两个临时变量left和right,分别用来计数以i为中心向左向右取字符。换个角度看,以i为中心分别向左右找相等的字符对,也可以看作以i为中心,向左右已经找到P[i]个满足回文字符串要求的字符后,再各向左右一位继续找下一对,因此,在不引入临时变量的情况下,上面的代码也可以写成这样(请记住这个表达,在后面的情况中这个思想非常重要!!!)
P[i]=0;
while(T[ i + 1 + P[0]] == T[ i - 1 - P[0]])
P[i]++;上面的代码一写出来,就会发现一个问题,这个循环在执行到第2次的时候,while中==表达式的右值将是T[i-1-P[i]] = T[1-1-1] = T[-1],很明显,数组越界了。
那么为什么会发生这个情况?又应该如何避免呢?
会发生这种情况是因为在代码中没有对字符串下标移动的位置进行判断(是否已到达起点或末尾),而只是进行简单的照镜子式配对判断。那么如何解决这个问题呢?有2中方式:
第一种,每次进行下标移动的时候都判断一下是否越界,虽然可以解决问题,但总是觉得这个解法太普通,而且判断也会拉低效率。
于是伟大的Manacher算法给出了第二种解决方法:在根据原字符串S生成字符串T的时候,在T的首尾分别添加一个特殊字符,于是刚才的数据就变成了这个样子。
在新的字符串T中执行while(T[i+1=P[i]] == T[i-1-P[i]),循环最终一定会在T[i]的值为“^"或者”$“的时候结束或者还没有到这两个位置就已经结束了,因为“^"和”$“都是字符串中的唯一字符。
情况二 :在T[i]之前,字符串T中存在子回文字符串,但是T[i]为止上的字符不包含在前面的任何子串中
如字符串T中的倒数第2个c,即T[22]。虽然其左侧有不止一串回文子字符串(例如”#a#“, "#b#", "#a#b#c#b#a#b#c#b#a#"),但是下图中画圈的c本身并没有包含在其中任何一个子字符串中。因此,以c为中心点的回文字符串的计算方法与情况一相同,即逐一比较c两侧的字符是否相同,若相同,则P[22]+1。代码实现也与情况一完全相同。
情况三 :第三种情况也是最复杂的一种情况,即在T[i]之前,字符串T中存在子回文字符串,而且T[i]为包含其中的某个子串中
如下图中的b和c,他们都被包含在回文子字符串”#a#b#c#b#a#b#c#b#a#“中,但是它们又分属不同的两种状况,接下来一一分析。
先看第一个,从下图中,可以很明显的看出, P[14] = P[10] = 1。这种情况可以总结为,如果T[i]属于一个回文字符串,但是T[i]与该回文字符串最右端字符的距离不大于P[i'](i'与i的关系如图示,它们是以C为中心的镜面对称点),那么P[i]等于P[i']。
P[i] = R - i;
while(T[i+1+P[i] == T(i-1-P[i]))
P[i]++;int mirrorIndex = 2 * cIndex - i;
//We assume there's a Palindromic string which centers at cIndex.
P[i] = (rightEdge > i) ? min(rightEdge-i, P[mirrorIndex]) : 0;
//Try to find out the Palindromic string which center is i
while(T[i + 1 + P[i]] == T[i - 1 - P[i]])
P[i]++; 到这里,整个算法最复杂的部分基本上都讲完了,还剩下一个重要的点,对于任何一个T[i]如何确定那个C从而找到T[i']。
if((i + P[i]) > rightEdge)
{
//Palindromic string centers at cIndex even cannot cover T[i],
//so cannot conver the right parts. so move cIndex to i and update rightEdge.
cIndex = i;
rightEdge = i + P[i];
}
通过数组P找到回文字符串在原始字符串中的起始点位置
最后,需要通过数组P从原始字符串S中找到这个最长子回文字符串,即代码中的最后一行return语句。可以用来进行计算的输入就是:找到的回文字符串的中心点的位置(centerIndexOfMax)以及整个回文字符串的长度(maxLen)。
首先要找到回文字符串在新字符串中的起始点。回文字符串的起点一定在字符串中心点的左侧,因此要用中心点位置centerIndexOfMax减掉左侧回文字符的长度(即maxLen/2)。但是由于新字符串对原始字符串进行了字符添加(在每个字符前添加一个#),因此在新字符串中,回文串中心点左侧回文字符的长度就是实际长度的2倍,即maxLen。所以,回文字符串的起点在新字符串中的起始点位置就是
startPos'' =centerIndexOfMax- maxlen
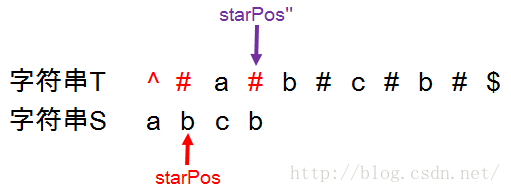
找到回文字符串在新字符串中的起始点后,再来看该点与原始字符串中回文字符的起始点位置的关系。
从上图不难看出,starPos''与starPos之间所差的就是新字符串T对原始字符串S添加的^和#。因为^只是在字符串开头添加了一次以防止溢出,因此直接减掉即可(即 -1),而#则是在每个字符前都添加了一次,因此导致字符串实际长度增加了1倍,从而Index的值也增加了1倍,因此原始Index应该是字符串T中的(Index -1)/ 2。综上得到回文字符串在原始字符串中的起始位置为:
startPos =(startPos''- 1)/ 2
在原始代码中(75行开始),作者用了一个时间复杂度为O(N)的循环,通过数组P找到最长回文子串的起始点以及长度。为了减少一次循环,我在查找子串并生成P的时候,就已经直接进行了标记。
最后的最后,再啰嗦一句,为什么函数的参数是const string&。这是为了避免函数调用时的字符串拷贝以及防止函数修改原字符串。