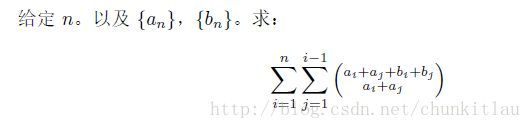【jzoj5358】【NOIP2017提高A组模拟9.12】【BBQ】

description

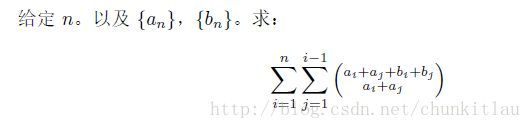
solution

可以发现组合数的意义就是在二维平面上一个点只能往上往右走走到另一个点的方案数，这个问题可以用递推来解决，相当于在(-a[i],-b[i])上都加一，求f(a[i],b[i])的和，减去i，j相等的情况再除以二即可。

code

#include
#include
#include
#include
#define LF double
#define LL long long
#define ULL unsigned int
#define fo(i,j,k) for(int i=j;i<=k;i++)
#define fd(i,j,k) for(int i=j;i>=k;i--)
#define fr(i,j) for(int i=begin[j];i;i=next[i])
using namespace std;
int const mn=2*1e5+3,mm=8*1e3,mo=1e9+7;
int n,a[mn],b[mn],fact[mm+3],ni[mm+3],f[4000+5][4000+5];
int c(int x,int y){
    return 1ll*fact[x]*ni[y]%mo*ni[x-y]%mo;
}
int Pow(LL x,int y){
    LL z=1;
    while(y){
        if(y&1)z=z*x%mo;
        x=x*x%mo;
        y>>=1;
    }
    return z;
}
int main(){
    //freopen("a.in","r",stdin);
    //freopen("a.out","w",stdout);
    freopen("d.in","r",stdin);
    freopen("d.out","w",stdout);
    scanf("%d",&n);
    int bit=2*1e3+1;
    fo(i,1,n)scanf("%d%d",&a[i],&b[i]),f[bit-a[i]][bit-b[i]]++;
    fact[0]=1;
    fo(i,1,mm)fact[i]=1ll*fact[i-1]*i%mo;
    ni[mm]=Pow(fact[mm],mo-2);
    fd(i,mm-1,0)ni[i]=1ll*ni[i+1]*(i+1)%mo;
    int ans=0;
    fo(i,1,bit*2)fo(j,1,bit*2)f[i][j]=(1ll*f[i][j]+f[i-1][j]+f[i][j-1])%mo;
    fo(i,1,n)ans=(ans+f[bit+a[i]][bit+b[i]])%mo;
    fo(i,1,n)ans=(ans-c(a[i]*2+b[i]*2,a[i]*2))%mo;
    printf("%d",(1ll*ans*Pow(2,mo-2)%mo+mo)%mo);
    return 0;
}