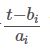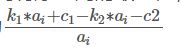HDU6274&&2017CCPC杭州K Master of Sequence

问题 K: Master of Sequence

时间限制: 10 Sec  内存限制: 128 MB
提交: 97  解决: 31
[提交] [状态] [命题人:admin]

题目描述

There are two sequences a1,a2,...,an , b1,b2,...,bn . Let 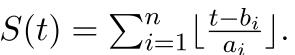. There are m operations within three kinds as following:
• 1 x y: change value ax to y.
• 2 x y: change value bx to y.
• 3 k: ask min{t|k≤S(t)}

 

输入

The first line contains a integer T (1≤T≤5) representing the number of test cases.
For each test case, the first line contains two integers n (1≤n≤100000), m (1≤m≤10000).
The following line contains n integers representing the sequence a1,a2,...,an .
The following line contains n integers representing the sequence b1,b2,...,bn .
The following m lines, each line contains two or three integers representing an operation mentioned above.
It is guaranteed that, at any time, we have 1≤ai≤1000, 1≤bi,k≤109 . And the number of queries (type 3 operation) in each test case will not exceed 1000.

 

输出

For each query operation (type 3 operation), print the answer in one line.

 

样例输入

复制样例数据

2
4 6
2 4 6 8
1 3 5 7
1 2 3
2 3 3
3 15
1 3 8
3 90
3 66
8 5
2 4 8 3 1 3 6 24
2 2 39 28 85 25 98 35
3 67
3 28
3 73
3 724
3 7775

样例输出

17
87
65
72
58
74
310
2875

 

 

思路：题目的重点是解决查询的复杂度，对于可以化简为。

设t=k1*ai+c1.  b=k2*ai-c2.            由于a数组范围为只有1000，我们可以通过预处理求出在1000范围 所有的 ai和c2,对于每个t它的c1是固定的。

#include
using namespace std;
typedef long long LL;
const int N=100100;
int a[N],b[N],num[1010][1010],n; //num[x][y]表示对于所有a[i]==x时的b[i]%a[i]余数大于等于y的数目
bool check(LL x,LL s) 
{
    LL ret=0;
    for(int i=1; i<=1000; i++)
    {
        ret+=x/i*num[i][0]; //num[i][0]为a数组中等于i的数的个数
        ret-=num[i][x%i+1];  //减掉所有 c1>1;
        if(check(mid,x))
            r=mid;
        else
            l=mid+1;
    }
    return l;
}
int main()
{
    int TA,T,x,y,z;
    LL ret;
    scanf("%d",&TA);
    while(TA--)
    {
        scanf("%d%d",&n,&T);
        ret=0;
        for(int i=1; i<=1000; i++)
            for(int j=0; j=0; j--)
                num[i][j]+=num[i][j+1];
        while(T--)
        {
            scanf("%d%d",&z,&x);
            if(z==1)
            {
                scanf("%d",&y);
                for(int i=b[x]%a[x]; i>=0; i--)
                    num[a[x]][i]--;
                for(int i=b[x]%y; i>=0; i--)
                    num[y][i]++;
                ret-=(b[x]/a[x]);
                ret+=(b[x]/y);
                a[x]=y;
            }
            else if(z==2)
            {
                scanf("%d",&y);
                for(int i=b[x]%a[x]; i>=0; i--)
                    num[a[x]][i]--;
                for(int i=y%a[x]; i>=0; i--)
                    num[a[x]][i]++;
                ret-=(b[x]/a[x]);
                ret+=(y/a[x]);
                b[x]=y;
            }
            else
            {
                printf("%lld\n",solve(ret+x));
            }
        }
    }
}