奇异值分解
我觉得线性代数中最主要的概念是基变换和矩阵分解。矩阵分解的本质就是基变换。选择不同的基,可以将矩阵分解为不同的形式。几种不同的线性变换
A A A是一个 m ∗ n m*n m∗n的矩阵,与 A A A相关的4个空间如下:
列空间C(A), 行空间R(A), 零空间N(A), A T A^T AT的零空间 N ( A T ) N(A^T) N(AT)
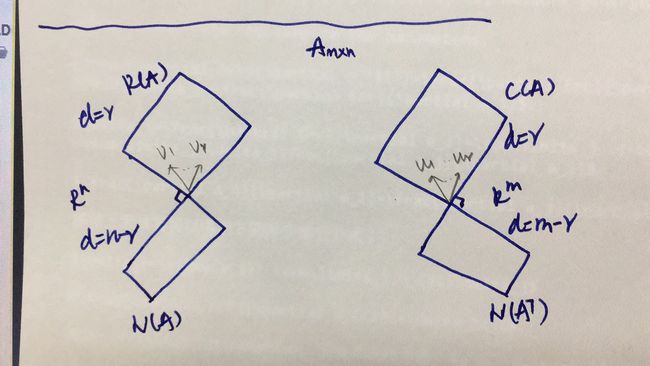
奇异值分解是要在行空间和列空间各找一组基。
one set of basis of the row space of A: v 1 , v 2 , . . . , v r v_1, v_2,...,v_r v1,v2,...,vr, and one set of basis of the column space of A: u 1 , u 2 , . . . , u r u_1, u_2,...,u_r u1,u2,...,ur,其中 r r r是列空间和行空间的维度。
A v i = σ i u i , i = 1 , 2 , . . . , r Av_i=\sigma_i u_i, i=1,2,...,r Avi=σiui,i=1,2,...,r
V = [ v 1 , v 2 , . . . , v r ] , U = [ u 1 , u 2 , . . . , u r ] V=[v_1,v_2, ...,v_r], U=[u_1,u_2, ..., u_r] V=[v1,v2,...,vr],U=[u1,u2,...,ur]
A V = U Σ , A = U Σ V T AV=U\Sigma, A=U\Sigma V^T AV=UΣ,A=UΣVT
A = U Σ V T , A T = V Σ U T A=U\Sigma V^T, A^T=V\Sigma U^T A=UΣVT,AT=VΣUT
A A T = U Σ 2 U T , A T A = V Σ 2 V T AA^T=U\Sigma^2U^T, A^TA=V\Sigma^2 V^T AAT=UΣ2UT,ATA=VΣ2VT,所以 U , V , Σ U,V,\Sigma U,V,Σ可以通过 A A T , A T A AA^T, A^TA AAT,ATA的特征值,特征向量求得。因为是对称矩阵,所以一定存在。
应用
Principle Component Analysis, PCA
主成分分析
这里有详细的推导,也是Ali教授讲的,很好
Latent Semantic Indexing, LSI
latent semantic analysis (LSA)
隐语义检索
参考:Information Retrieval Algorithms and Heuristics, David A. Grossman, Ophir Frieder 2.6 Latent Semantic Indexing
用一个矩阵来描述词term和文章doc的关联性。在这个矩阵中,每一行对应一个词,每一列对应一个文档。设有 m m m个词, n n n篇文章,term-document matrix可以表示如下, a i j a_{ij} aij表示第j个词在第i篇文档中出现次数tf,或tf-idf值。
A = [ a 11 . . . a 1 n . . . a i 1 . . . a i n . . . a m 1 . . . a m n ] A= \left[ \begin{matrix} a_{11} & ... & a_{1n} \\ ... \\ a_{i1} & ... & a_{in} \\ ... \\ a_{m1} & ... & a_{mn} \\ \end{matrix} \right] A=⎣⎢⎢⎢⎢⎡a11...ai1...am1.........a1nainamn⎦⎥⎥⎥⎥⎤
如下图所示,是与 A A A相关的四个子空间,文章在列空间,词在行空间,关键是 A A A不是满秩的,我们所看到的文章和词是在子空间中,零空间中的分量为0,所以可以不损失信息的压缩(解释一下,word是在m维空间,但它存在于一个维度维r的子空间,比如三维空间中的一面墙,墙这个平面是二维的)。 A t = d At=d At=d, t t t是词term, d d d是文档document。
对它进行奇异值分解 A = U Σ V T A=U\Sigma V^T A=UΣVT
import numpy as np
A = np.matrix(
[[1, 1, 1], [0, 1, 1], [1, 0, 0], [0, 1, 0], [1, 0, 0], [1, 0, 1], [1, 1, 1], [1, 1, 1], [1, 0, 1], [0, 2, 0],
[0, 1, 1]])
U, S, VT = np.linalg.svd(A, full_matrices=False)
B = U * np.diag(S) * VT
print(np.isclose(A, B))
U = [ − 0.42012157 − 0.07479925 − 0.04597244 − 0.29948676 0.20009226 0.40782766 − 0.12063481 − 0.27489151 − 0.4538001 − 0.157561 0.30464762 − 0.2006467 − 0.12063481 − 0.27489151 − 0.4538001 − 0.26256057 − 0.37944687 0.15467426 − 0.42012157 − 0.07479925 − 0.04597244 − 0.42012157 − 0.07479925 − 0.04597244 − 0.26256057 − 0.37944687 0.15467426 − 0.315122 0.60929523 − 0.40129339 − 0.29948676 0.20009226 0.40782766 ] Σ = [ 4.09887197 0. 0. 0. 2.3615708 0. 0. 0. 1.27366868 ] V T = [ − 0.49446664 − 0.64582238 − 0.58173551 − 0.64917576 0.71944692 n − 0.24691489 − 0.57799098 − 0.25555741 0.77499473 ] U=\left[\begin{matrix} -0.42012157 & -0.07479925 & -0.04597244 \\ -0.29948676 & 0.20009226 & 0.40782766 \\ -0.12063481 &-0.27489151& -0.4538001 \\ -0.157561 & 0.30464762 & -0.2006467 \\ -0.12063481 & -0.27489151 & -0.4538001 \\ -0.26256057 & -0.37944687 & 0.15467426 \\ -0.42012157 & -0.07479925 & -0.04597244 \\ -0.42012157 & -0.07479925 & -0.04597244 \\ -0.26256057 & -0.37944687 & 0.15467426 \\ -0.315122 & 0.60929523 & -0.40129339 \\ -0.29948676 & 0.20009226 & 0.40782766 \end{matrix}\right] \\\\ \Sigma = \left[\begin{matrix} 4.09887197 & 0. & 0. \\ 0. & 2.3615708 & 0. \\ 0. & 0. & 1.27366868 \end{matrix}\right] \\ V^T= \left[\begin{matrix} -0.49446664 & -0.64582238 & -0.58173551\\ -0.64917576 & 0.71944692 & n-0.24691489 \\ -0.57799098 & -0.25555741 & 0.77499473 \end{matrix}\right] U=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡−0.42012157−0.29948676−0.12063481−0.157561−0.12063481−0.26256057−0.42012157−0.42012157−0.26256057−0.315122−0.29948676−0.074799250.20009226−0.274891510.30464762−0.27489151−0.37944687−0.07479925−0.07479925−0.379446870.609295230.20009226−0.045972440.40782766−0.4538001−0.2006467−0.45380010.15467426−0.04597244−0.045972440.15467426−0.401293390.40782766⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤Σ=⎣⎡4.098871970.0.0.2.36157080.0.0.1.27366868⎦⎤VT=⎣⎡−0.49446664−0.64917576−0.57799098−0.645822380.71944692−0.25555741−0.58173551n−0.246914890.77499473⎦⎤
上面对例子中: d 1 = A [ 1 0 0 ] d_1=A\left[\begin{matrix} 1 \\ 0 \\ 0 \end{matrix}\right] d1=A⎣⎡100⎦⎤,词空间(A的行空间)中的 [ 1 , 0 , 0 ] [1, 0, 0] [1,0,0]代表.
t是词到向量,d是文档的向量;选择新的基后,词向量用 t ′ = V T t t'=V^Tt t′=VTt表示,文档用 d ′ = U T d d'=U^Td d′=UTd表示;书中说新的文档用 Σ − 1 U T d \Sigma^{-1}U^Td Σ−1UTd表示,这其实是将新的文档向量反射到了新到词空间。我觉得书中这样表示是为了减少计算,这样 V V V的每一行就对应原来的每篇文档。不用再计算了,一次奇异值分解,就得到了每篇文档新的表示形式。
以词term为例,原来的基是 I I I,用奇异值分解后选择的基是 V = [ v 1 , v 2 , . . . , v r , v r + 1 , . . . , v n ] V=[v_1,v_2, ...,v_r,v_{r+1},...,v_{n}] V=[v1,v2,...,vr,vr+1,...,vn],前r个向量是奇异值分解的基,后面 n − r n-r n−r个向量在A的零空间中任意一组基,term原来用 x x x表示,变换后用 x ′ x' x′表示,进行基变换:
I x = V x ′ x ′ = V T x x ′ = [ v 1 T ⋮ v r T v r + 1 T ⋮ v n T ] x = [ v 1 T x 1 ⋮ v r T x r v r + 1 T x r + 1 ⋮ v n T x n ] = [ v 1 T x 1 ⋮ v r T x r 0 ⋮ 0 ] Ix=Vx' \\ x'=V^Tx \\ x'=\left[ \begin{matrix} v_1^T \\ \vdots\\v_r^T\\v_{r+1}^T \\ \vdots \\ v_n^T \\ \end{matrix} \right]x=\left[ \begin{matrix} v_1^Tx_1 \\ \vdots \\ v_r^Tx_r \\ v_{r+1}^Tx_{r+1} \\ \vdots \\ v_n^Tx_n \\ \end{matrix} \right] =\left[ \begin{matrix} v_1^Tx_1 \\ \vdots \\ v_r^Tx_r \\ 0 \\ \vdots \\ 0 \\ \end{matrix} \right] Ix=Vx′x′=VTxx′=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡v1T⋮vrTvr+1T⋮vnT⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤x=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡v1Tx1⋮vrTxrvr+1Txr+1⋮vnTxn⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡v1Tx1⋮vrTxr0⋮0⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
原来 n n n维的 x x x,就可以用 r r r维的 x ′ x' x′表示。