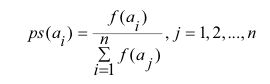遗传算法入门详解

csdn的第一篇博文介绍遗传算法入门，希望对刚刚学习遗传算法的同学能有所帮助。

下面是参考于维基百科对遗传算法的定义：遗传算法是一种解决最优化问题的启发式算法，借鉴了进化生物学的一些现象，其中包括遗传，突变，自然选择和杂交等。通俗来讲，遗传算法就是在一群问题的候选解中通过各种操作寻找最优解（或近似最优解）的过程，这个过程中用到了模拟生物遗传学的知识。

1. 遗传算法（Genetic algorithm  ，GA）的组成：

种群（population）：生物进化的最小单位，包含许多个个体。

个体（individual）：种群中的一个个体，含有某些基因片段。

基因（gene）：一个遗传变量

编码（encode）：讲个体描述成机器可以识别的模式（0，1字符串或者浮点数）

交叉（crossover）：两个被选中的个体，通过交叉生成两个新个体，替换原来的两个个体

变异（mutation）：对一个个体基因变异，生成新个体替换原来的老个体。

适应度（relative fitness）：个体对环境的适应能力，同样代表该个体的生命力。 

2. 遗传算法的思想：

遗传算法模拟生活中的遗传现象，类似于环境对生物的自然选择，优胜劣汰。我们用该个体的适应度（fitness）代表该个体对环境的适应能力，适应度高代表个体优秀，适应度低代表个体弱。我们通过适应度为基础对种群的个体进行概率选择，适应度高的个体被选中进入下一代的概率高，适应度低的个体被选中的概率低。那么随着下一代个体总体上比上一代个体更加优秀，最后选择出最优秀的个体作为最优解。

3. 遗传算法的基本步骤：

开始 BEGIN

初始化第0代种群 Initialization

评估初始种群中每个个体的适应度Evaluation

循环操作直到找到最优解或循环到终止条件While（obtain solution or termination）

种群进入下一代 generation＋＋

选择操作 Selection

交叉操作 Crossover

突变操作 Mutation

评估这一代中每个个体进行适应度Evaluation

终止循环 END

终止算法 END GA

4.遗传算法中选择操作的过程：

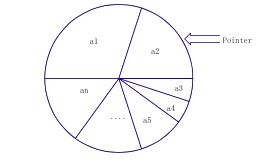
遗传算法的选择过程一般使用轮盘赌算法（Roulette wheel）或竞争选择算法（Tournament selection），我们来一一介绍

轮盘赌算法就是把一个圆形的轮盘分割成若干扇形，每一扇型代表相应的意义。在遗传算法中，我们用适应度评估个体，所以，我们先计算出所有个体的适应度，把所有个体的适应度相加得到一个该代总适应度，我们用一整个轮盘就代表该代的总适应度，那么组成这个轮盘的一一个小扇形就代表组成这一代种群的一个个个体，那么扇型的面积大小代表着该个体的适应度情况，适应度越高，扇形面积越大；适应度越低，扇形的面积越小。表示如下图（图片参考自论文“Comparison of performance between Different Selection Strategies on Simple Genetic Algorithm” ）：

                     

竞争选择算法是一种随机择优选择算法，假设这一代种群中总共有N个个体，那么竞争选择的过程是   第一步：从这N个个体中随机的选择［1～N］个个体，假设选择了n个个体，那么从这n个个体中选赞个体适应度最大的那一个进入下一代群体。 第二步 ： 执行第一步N次，总共选择N个个体组成下一代群体。特点：根据适应度的大小，有的适应度大的个体被选择了好几次，而有的适应度小的个体，则一次都没有被选中，被淘汰。

ps：遗传算法的选择操作影响遗传算法的收敛性，使用竞争选择（tournament selection）收敛性快于轮盘选择（roulette wheel selection），选择算法性能前者明显大于后者。

5. 遗传算法的交叉过程：

遗传算法的交叉可以加快遗传算法的收敛，更快的找出最优解。在交叉过程中，交叉点是随机选择的，例如如下交叉操作，交叉点是x＝5.

交叉前：

S1＝00111｜ 101

S2＝11101｜ 011

交叉后：

S1＝00111｜ 011

S2＝11101｜ 101

6. 遗传的变异操作过程：

遗传算法的变异操作可以保持基因的多样性，加快遗传算法收敛，减少算法沉浸在局部最优解的可能，尽可能找到全局最优解。而且变异操作的变异点是随机选择的，例如x＝5.

变异前：

S＝0100 1101

变异后：

S＝0100 0101

7. 应用和简单举例：

遗传算法已被广泛应用到模式识别（patter recognition），机器人学（robotics），人工生命（artificial life）等众多领域。

我们下面简单的举一个例子，帮助大家理解遗传算法。

使用遗传算法求解y ＝ －x^2 ＋32*x 在区间［0，31］的最大值

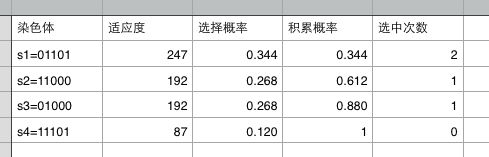
我们可以根据数学公式求解，最优解为当X ＝ 16 的时候，Y＝ 256. 我们规定，当Y的差值在3以内的时候（253

接下来我们用遗传算法求解，并显示出详细的过程。（参数：种群规模：4，交叉率：50%，变异率：0.05）

解：（1）选择合适的编码方案，我们选择5位二进制编码，这样可以把区间［0，31］中的个体全部表示出来，二进制编码是遗传算法的一种简洁有效的编码方案。

随机的从种群［0，31］中选择4个数作为初始种群，例如选择S1=13，S2=24，S3=8，S4=29.

（2）定义适应度函数，定义适应度函数是遗传算法的重要部分，一个好的适应度函数可以有效快速的解决问题。我们定义适应度函数为f（x）＝x^2.

（3）求每个个体的适应度值，求总适应度值，和每个个体的选择概率.

个体编码：

S1=(01101) S2=(11000)

S3=(01000) S4=(11101)

个体适应度：

f(s1)= -13^2 + 32*13 = 247 f(s2)= -24^2 + 32*24 = 192

f(s3)= -8^2 + 32*8 = 192 f(s4)= -29^2 + 32*29 = 87

总适应度：

t ＝ 718

每个个体的选择概率为：

p(s1)= 247/718 = 0.344 p(s2)= 192/718 = 0.268

p(s3)= 192/718 = 0.268 p(s4)= 87/718 = 0.120

使用轮盘赌选择算法选择对当前群体执行选择，计算累计概率，生成0-1内的四个随机数，选择下一代群体。

生成的4个随机数为r1=0.550126，r2=0.138947, r3=0.869082, r4=0.301439

所以选中的下一代群体为

s1' = 11000, s2' = 01101, s3' = 01000,  s4' = 01101 (s1 被选中两次）

（4）交叉操作，交叉概率为50％，所以选择2个后代进行染色体交叉

设s1' 与 s2'  交叉，交叉节点随机选择

交叉前：

s1' = 110｜00

s2' = 011｜01

交叉后

s1‘ ＝ 110｜01

s2’ ＝ 011｜00

（5）变异操作，变异概率为0.05，那么这一代5＊4*0.05 ＝ 1，那么就是说，每一代中有一个二进制数发生反转突变。

假设s1‘发生突变

s1‘ ＝ 11001 突变为 s1‘ ＝ 11101

于是得到第二代种群，并用第二个种群替换第一个种群：

s1 = 29（11101）, s2 = 12（01100）, s3 = 8（01000）, s4 = 13（01101）

遗传算法过程如下：

选择结果为s1' = 01100, s2' = 01100, s3' = 01000,  s4'= 01101

交叉操作为s2'与s3'，交叉后s2' = 01100, s3' = 01000.

变异操作 选择s4' = 01101 变异为s4' = 01111。

我们计算s4‘的适应度值为 255.满足近似最优解的条件，那么我们把个体s ＝ 01111，作为该问题的近似最优解。

综上例证，虽然我们最后没有找到标准最优解，但是我们找到了近似最优解，两者的差距满足条件要求，解决了该问题。

所以，遗传算法是一个元启发式算法，该算法不能保证一定可以找到最优解，但是在杂乱无章的群体中逐步寻找近似最优解还是有着很好的效率和准确性（相比于大多数盲目搜索算法），当前遗传算法面临的一个问题就是过早收敛（又称作早熟），还有待解决。

总结：这是一篇关于遗传算法入门的文章，讲解比较罗嗦，目的是希望初学者可以更好的理解。

文章内容如有不准确之处，一经发现，马上修改，还请各位不吝指正，谢谢。