Wavel Sequence
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 362 Accepted Submission(s): 175
Problem Description
Have you ever seen the wave? It's a wonderful view of nature. Little Q is attracted to such wonderful thing, he even likes everything that looks like wave. Formally, he defines a sequence
a1,a2,...,an as ''wavel'' if and only if
a1<a2>a3<a4>a5<a6...

Picture from Wikimedia Commons
Now given two sequences
a1,a2,...,an and
b1,b2,...,bm, Little Q wants to find two sequences
f1,f2,...,fk(1≤fi≤n,fi<fi+1) and
g1,g2,...,gk(1≤gi≤m,gi<gi+1), where
afi=bgi always holds and sequence
af1,af2,...,afk is ''wavel''.
Moreover, Little Q is wondering how many such two sequences
f and
g he can find. Please write a program to help him figure out the answer.
Input
The first line of the input contains an integer
T(1≤T≤15), denoting the number of test cases.
In each test case, there are
2 integers
n,m(1≤n,m≤2000) in the first line, denoting the length of
a and
b.
In the next line, there are
n integers
a1,a2,...,an(1≤ai≤2000), denoting the sequence
a.
Then in the next line, there are
m integers
b1,b2,...,bm(1≤bi≤2000), denoting the sequence
b.
Output
For each test case, print a single line containing an integer, denoting the answer. Since the answer may be very large, please print the answer modulo
998244353.
Sample Input
Sample Output
10
Hint
(1)f=(1),g=(2). (2)f=(1),g=(3). (3)f=(2),g=(4). (4)f=(3),g=(5). (5)f=(1,2),g=(2,4). (6)f=(1,2),g=(3,4). (7)f=(1,3),g=(2,5). (8)f=(1,3),g=(3,5). (9)f=(1,2,3),g=(2,4,5). (10)f=(1,2,3),g=(3,4,5).
Source
2017 Multi-University Training Contest - Team 4
题意:给出一个有n(<=2000)个数字的序列 a(ai <=2000) 再给出一个有m(m<=2000)个数字的序列 b (bi<=2000) ,定义波浪序列为:x1x3=1)使得每个a_fi = b_gi,同时满足a_f1,a_f2,a_f3……a_fk为波浪序列。求不同的fg映射有多少种选取方式。
a,b中分别从前向后选取k个数字。然后相对应的 a 中选择的每个位置的数字要和 b 中选择的对应位次的数字相同。(当然如果a数组出现过x,而b没有出现过x,显然x不可能被选取),而 f 、g 则是相对应的下标。要满足选取出来的这个数字序列是一个波浪序列。显然波浪序列中的数字分成两种:波峰和波谷。
总体来说,这个题就是a、b数组之间的匹配问题,同时满足是一个波浪序列。
则:
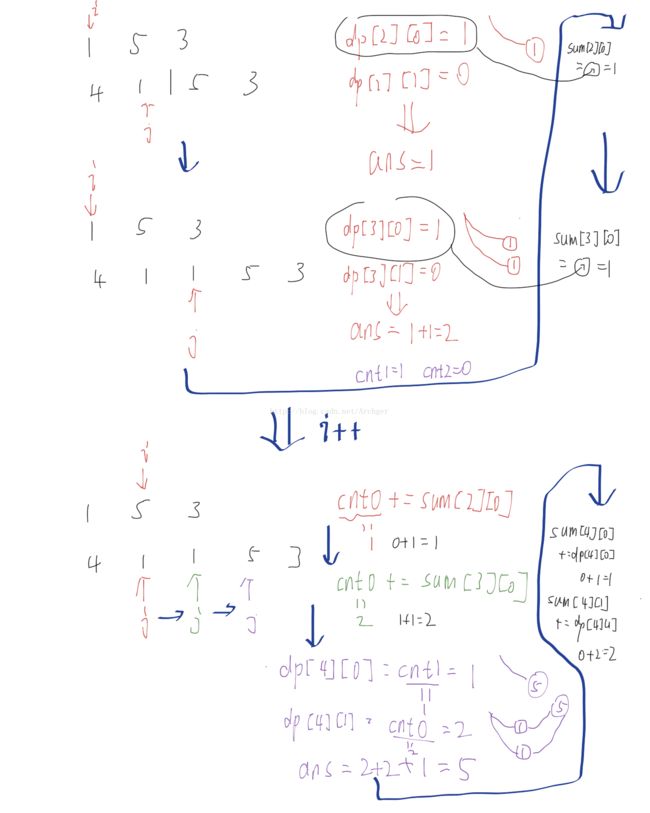
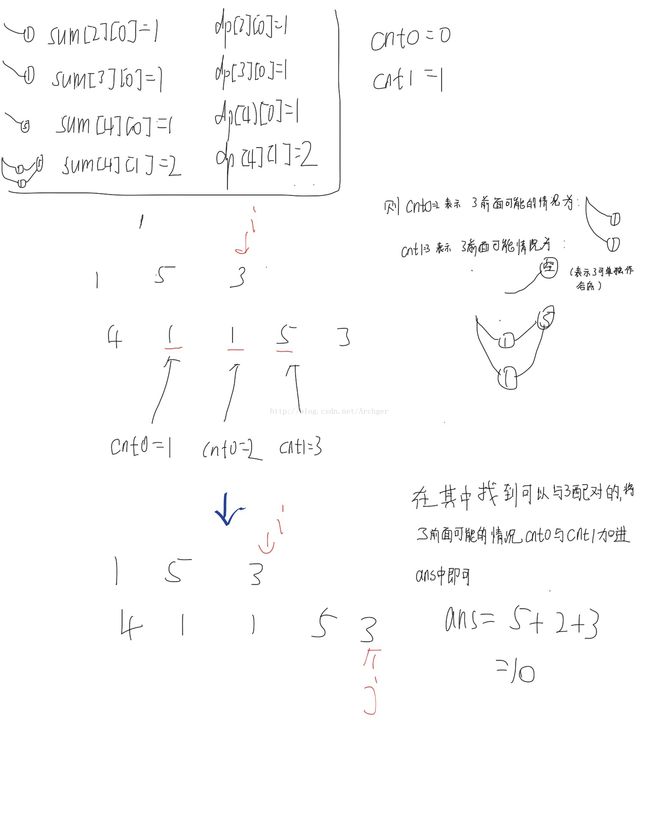
dp[i][j][0]表示以a[i]和b[j]为公共序列结尾且为波谷的情况总和。
dp[i][j][1]则表示波峰的情况总和。
sum[i][j][0]表示sum(dp[k][j][0] | 1<=k<=i-1)
sum[i][j][1]则表示sum(dp[k][j][1] | 1<=k<=i-1) (相当于固定b[j]这个数字,然后将所有可能性加起来)
那么这个过程中只要不断判断这个数字其前面可能的情况(若其为波峰则判断其前可满足作为波谷的数量cnt0,反之亦然),然后判断这个数字能不能加进这个波浪中不断记录结果即可。
注意因为第一次必须为上升,则表示第一个数字前为波峰所以cnt1=1,cnt0=0
这个题有两点值得借鉴:
1、动态规划递推过程中用波峰波谷作为状态转移的关键,然后进行递推
2、用sum来优化其前相加的结果,减少重复的相加运算。
以下是样例的递推过程,蓝色粗线代表程序执行过程,旁边的线代表当前所记录波浪的状态:
#include
#include
#include
#include
#include
#include
#include
可借鉴:点击打开链接的思路


