【清华集训2017模拟】ces

Description:

1<=n<=1e5,1<=q<=m<=2e5

题解：

首先把用tajan把桥边全部找出来，桥边会把图分成若干个双联通分量。
把每个双联通分量并成一个点，桥边作为边，这会构成一棵树。

显然，对于每个询问加k条边最多能去掉多少条桥边，就是用k条简单路径去覆盖这棵树，最多能覆盖多少条边。

有一个很优的贪心，把k按1-q做，每次找到树的直径，答案加上直径的长度，把直径压成一个点，继续做k+1的。

但是这个贪心显然有反例：

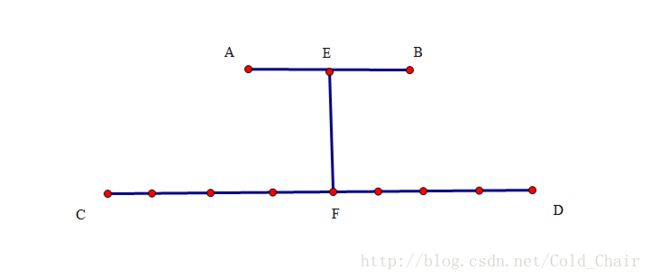
如上图：
按贪心，第一次我们会选择C->D,第二次选择A->B,第三次选择E->F。
但是，明显第一次选择A->E->F->D，第二次选择B->E->F->C,会使得k=2时答案最优。

于是集训队大爷出题人的“标程”是伪的。

大爷大概给了个dfs序的伪做法，建棵线段树，区间[l..r]表示dfs序为[l..r]的点所构成的子树的直径，根据直径的一个性质，两颗子树合并后的新的树直径的两个端点一定是原来两颗子树的四个直径端点的两个，所以用O(log n)求lca，这是O(n log n log n)的.

对于每次把直径压成一个点，其实不用这么想，想象把u->fa[u]这条边删掉.就相当于把u的子树的深度减1，显然它的子树的直径不会变，打个lazy_tag就好了。

讲了这么多，都是伪的。

来讲讲镇中大佬的做法：
假设我第一次选了直径C->D，第二次选了A->B,实际上这是可以合并的,就可以交叉合并成A->E->F->D，B->E->F->C。
所以我可以在第一次搞出直径的基础上，再选两条从直径出发的最长的互不相交的长链，每次都是如此。
所以以直径的端点为根，进行长链剖分，再将链按长度排序，依次选长的就好了。
长链剖分，和树链剖分类似，树链剖分重儿子的关键字是子树大小，改为子树的最深度即可。

代码较繁琐。

Code:

#include 
#include 
#include 
#define min(a, b) ((a) < (b) ? (a) : (b))
#define max(a, b) ((a) > (b) ? (a) : (b))
#define fo(i, x, y) for(int i = x; i <= y; i ++)
using namespace std;

const int N = 100005;

int n, m, q, x, y, sumq, ans;
int final[N], tot;
struct edge {
    int st, to, next;
}e[N * 4], c[N * 4];
int dfn[N], low[N], bz[N * 4], bd[N * 4], tt;
int f[N];
int fi[N], tp;

void link(int x, int y) {
    e[++ tot].next = final[x]; e[tot].st = x; e[tot].to = y, final[x] = tot;
    e[++ tot].next = final[y]; e[tot].st = y; e[tot].to = x, final[y] = tot;
}

void Init() {
    scanf("%d %d %d", &n, &m, &q);
    tot = 1;
    fo(i, 1, m) {
        scanf("%d %d", &x, &y);
        link(x, y);
    }
}

void dg(int x, int last) {
    bd[x] = 1; dfn[x] = ++ tt; low[x] = 1e9;
    for(int i = final[x]; i; i = e[i].next) {
        int y = e[i].to; if(i == (last ^ 1)) continue;
        if(bd[y]) {
            low[x] = min(low[x], dfn[y]);
        } else {
            dg(y, i);
            low[x] = min(low[x], low[y]);
            if(low[y] > dfn[x])
                bz[i] = bz[i ^ 1] = 1, sumq ++;
        }

    }
}

int find(int x) {
    return f[x] == x ? x : (f[x] = find(f[x]));
}

void bin(int x, int y) {
    if(find(x) != find(y)) f[f[x]] = f[y];
}

void tlink(int x, int y) {
    c[++ tp].next = fi[x], c[tp].st = x, c[tp].to = y, fi[x] = tp;
    c[++ tp].next = fi[y], c[tp].st = y, c[tp].to = x, fi[y] = tp;
}

void Build() {
    fo(i, 1, n) f[i] = i;
    fo(i, 1, n) for(int j = final[i]; j; j = e[j].next) if(!bz[j]) {
        bin(i, e[j].to);
    }
    tp = 1;
    fo(i, 2, tot) if((i & 1) && bz[i]){
        tlink(find(e[i].st), find(e[i].to));
    }
}

int d[N], dis[N], last[N], bx[N], tbx;

int Bfs(int x) {
    ++ tbx;
    d[1] = x; dis[x] = 0; d[0] = 1; bx[x] = tbx;
    for(int st = 1; st <= d[0]; st ++) {
        int x = d[st];
        for(int i = fi[x]; i; i = c[i].next)
            if(bx[c[i].to] != tbx) {
                bx[c[i].to] = tbx;
                dis[c[i].to] = dis[x] + 1;
                d[++ d[0]] = c[i].to;
                last[d[0]] = st;
            }
    }
    return d[d[0]];
}

int by[N], dep[N], sd[N], son[N], top[N];

void dg1(int x) {
//  printf("%d %d\n", x, dep[x]);
    by[x] = 1; sd[x] = dep[x];
    for(int i = fi[x]; i; i = c[i].next) {
        int y = c[i].to; if(by[y]) continue;
        dep[y] = dep[x] + 1;
        dg1(y);
        if(sd[y] > sd[son[x]]) son[x] = y;
        sd[x] = max(sd[x], sd[y]);
    }
    by[x] = 0;
}

void dg2(int x) {
    by[x] = 1;
    if(son[x] != 0) top[son[x]] = top[x], dg2(son[x]);
    for(int i = fi[x]; i; i = c[i].next) {
        int y = c[i].to; if(by[y] || y == son[x]) continue;
        top[y] = y; dg2(y);
    }
}

bool rank(int x, int y) {
    return x > y;
}

int main() {
    freopen("ces.in", "r", stdin);
    freopen("ces.out", "w", stdout);
    Init();
    dg(1, 0);
    Build();
    int xx = Bfs(find(1));
    dep[xx] = 1; dg1(xx);
    top[xx] = xx; dg2(xx);
    d[0] = 0;
    fo(i, 1, n) if(i == find(i) && son[i] == 0)
        d[++ d[0]] = dep[i] - dep[top[i]];
    sort(d + 1, d + d[0] + 1, rank);
    int ans = d[1]; printf("%d\n", ans);
    fo(i, 2, q) {
        if((i - 1) * 2 <= d[0]) ans += d[(i - 1) * 2] + 1;
        if(i * 2 - 1 <= d[0]) ans += d[i * 2 - 1] + 1;
        printf("%d\n", ans);
    }
}