从贝叶斯到卡尔曼

背景介绍

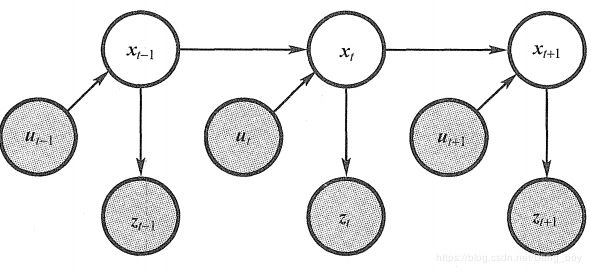
假设我们的模型是这个样子的
$$\{\begin{array}{ll}{x}_k=f(x_{k-1},u_k)+w_k& 预测方程\\ z_k=h(x_k)+v_k& 观测方程\end{array}$$
已知条件有在0时刻的分布$x_0$,所有时刻的运动输入$u_{1:k}$,所有时刻的观测$z_{1:k}$，然后我们要计算在k时刻的$x_k$的分布
$$P(x_k|x_0,u_{1:k},z_{1:k})$$

求解过程（贝叶斯滤波）

1. 将$P(x_k|x_0,u_{1:k},z_{1:k})$通过贝叶斯展开
   $$\begin{array}{rl}& P(x_k|x_0,u_{1:k},z_{1:k})\\ & =\frac{P(x_k,x_0,u_{1:k},z_{1:k})}{P(x_0,u_{1:k},z_{1:k})}\\ & =\frac{P(z_k|x_k,x_0,u_{1:k},z_{1:k-1})P(x_k|x_0,u_{1:k},z_{1:k-1})P(x_0,u_{1:k},z_{1:k-1})}{P(z_k|x_0,u_{1:k},z_{1:k-1})P(x_0,u_{1:k},z_{1:k-1})}\\ & =\frac{P(z_k|x_k,x_0,u_{1:k},z_{1:k-1})P(x_k|x_0,u_{1:k},z_{1:k-1})}{P(z_k|x_0,u_{1:k},z_{1:k-1})}\end{array}$$
2. 我们假设世界是马尔可夫的，即当前的状态只和上一刻有关，这样的话在$x_k$已知的情况下，就已经包含了$x_0,u_{1:k},z_{1:k-1}$的所有信息,即符合条件独立(此时的$x_k$是已知的了，是一个确定的状态了）$$P(z_k|x_k,x_0,u_{1:k},z_{1:k-1})=P(z_k|x_k)$$

3. 由于分母与$x_k$的取值无关，即不管$x_k$取什么值，分母都是定值，可以看成一个常量，即
   $$\eta ={P(z_k|x_0,u_{1:k},z_{1:k-1})}^{-1}$$

综上，可以得到
$$P(x_k|x_0,u_{1:k},z_{1:k})=\eta P(z_k|x_k)P(x_k|x_0,u_{1:k},z_{1:k-1})$$
将$P(z_k|x_k)$称为似然，将$P(x_k|x_0,u_{1:k},z_{1:k-1})$称为先验。到现在，我们可以通过观测方程求得似然，但是先验部分还没有办法直接求，接下来使用全概率公式引进$x_{k-1}$
$$\begin{array}{rl}& P(x_k|x_0,u_{1:k},z_{1:k-1})\\ & =\frac{{\sum }_{x_k-1}P(x_k,x_{k-1},u_{1:k},z_{1:k-1})}{P(x_0,u_{1:k},z_{1:k-1})}\\ & =\sum _{x_k-1}\frac{P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})P(x_0,u_{1:k},z_{1:k-1})}{P(x_0,u_{1:k},z_{1:k-1})}\\ & =\sum _{x_k-1}P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})离散形式\\ & =\int P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})d{x}_{k-1}连续形式\end{array}$$
综合上式，既可以得到贝叶斯滤波的表达式，记
$$bel(x_k)=P(x_k|z_{1:k},u_{1:k},x_0)$$
$$\overline{bel}(x_k)=P(x_k|z_{1:k-1},u_{1:k},x_0)$$
假设在这个世界是马尔可夫的，也就是当前的状态之和之前的状态有关，与之后的状态无关,且$x_{k-1}$已经包含了过去的所有信息，则
$$\begin{array}{rl}& bel(x)=P(x_k|x_0,u_{1:k},z_{1:k})\\ & =\eta P(z_k|x_k)P(x_k|x_0,u_{1:k},z_{1:k-1})\\ & =\eta P(z_k|x_k)\int P(x_k|x_{k-1},x_0,u_{1:k},z_{1:k-1})P(x_{k-1}|x_0,u_{1:k},z_{1:k-1})d{x}_{k-1}\\ & =\eta P(z_k|x_k)\int P(x_k|x_{k-1},u_k)P(x_{k-1}|x_0,u_{1:k-1},z_{1:k-1})d{x}_{k-1}用到了上面的假设\\ & =\eta P(z_k|x_k)\int P(x_k|x_{k-1},u_k)bel(x_{k-1})d{x}_{k-1}\\ & =\eta P(z_k|x_k)\overline{bel}(x_k)\end{array}$$
到这里已经成功的推导出了贝叶斯滤波算法。
接下来举一个例子来帮助理解

一只机器人在门的前面检测距离门的距离，估算门开或关，已知在没有任何条件的情况下，门打开或者关闭概率都是0.5。此时机器人检测到距离门的距离是0.5m，已知门打开的情况下，距离门0.5m的概率是0.6,门关闭的情况下，距离门0.5m的概率是0.3,求此时门打开的概率

这个问题比较简单，就是直接利用贝叶斯即可
$$\begin{array}{rl}& P(x_1=open|z_1=0.5m)\\ & =\frac{P(z_1|x_1)P(x_1)}{P(z_1|x_1)P(x_1)+P(z_1|\neg x_1)P(\neg x_1)}\\ & =\frac{0.6\ast 0.5}{0.6\ast 0.5+0.3\ast 0.5}=\frac{2}{3}\end{array}$$
也可以利用上述的结论
$$\begin{array}{rl}& bel(x_1=open)\\ & =P(x_1=open|x_0,z_1=0.5m)没有动作，所以只有z\\ & =\eta P(z_1|x_1)\sum _{x_0}P(x_1|x_0)bel(x_0)\\ & =\eta P(z_1|x_1)(P(x_1|x_0=open)P(x_0=open)+P(x_1|\neg x_0)P(\neg x_0))\\ & =\eta \ast 0.6\ast (1\ast 0.5+0\ast 0.5)=0.3\eta \end{array}$$

$$\begin{array}{rl}& bel(x_1=closed)\\ & =P(x_1=closed|x_0,z_1=0.5m)没有动作，所以只有z\\ & =\eta P(z_1|x_1)\sum _{x_0}P(x_1|x_0)bel(x_0)\\ & =\eta P(z_1|x_1)(P(x_1|x_0=open)P(x_0=open)+P(x_1|\neg x_0)P(\neg x_0))\\ & =\eta \ast 0.3\ast (0\ast 0.5+1\ast 0.5)=0.15\eta \end{array}$$
$$\begin{gathered} 0.15\eta +0.3\eta =0.45\eta =1 \\ bel(x_1=open)=0.3\eta =\frac{2}{3} \end{gathered}$$
两个方法求出来的结果是一样的。
同时注意这里的情况，这是只有观测，没有动作，所以世界是不会改变的，即原来的状态是什么样子的，便是什么样子的，所以先验部分只需要处理与$x_1$状态相同的情况即可。

在上面的基础，进行第二次观察，结果仍然是0.5m，求此时门开着的概率

$$\begin{array}{rl}& bel(x_2=open)\\ & =P(x_2=open|x_0,z_1=0.5m,z_2=0.5m)\\ & =\eta P(z_2|x_2)\sum _{x_1}P(x_2|x_1)bel(x_1)\\ & =\eta P(z_2|x_2)(P(x_2|x_1=open)P(x_1=open)+P(x_2|\neg x_1)P(\neg x_1))\\ & =\eta \ast 0.6\ast (1\ast \frac{2}{3}+0\ast \frac{1}{3})=0.4\eta \end{array}$$

$$\begin{array}{rl}& bel(x_2=closed)\\ & =P(x_2=closed|x_0,z_1=0.5m,z_2=0.5m)\\ & =\eta P(z_2|x_2)\sum _{x_1}P(x_2|x_1)bel(x_1)\\ & =\eta P(z_2|x_2)(P(x_2|x_1=open)P(x_1=open)+P(x_2|\neg x_1)P(\neg x_1))\\ & =\eta \ast 0.3\ast (0\ast \frac{2}{3}+1\ast \frac{1}{3})=0.1\eta \end{array}$$
$$\begin{gathered} 0.4\eta +0.1\eta =0.5\eta =1 \\ bel(x_2=open)=0.4\eta =0.8 \end{gathered}$$

假设机器人执行关门的动作有0.1的概率失败，即原本门是开着，有0.9的概率门关上了，0.1的概率门还开着，如果原本门关闭着，执行完动作后，门还是关着。现在机器人在前面的基础上，执行了关门的动作，问此时门开着的概率是多少？

$$\begin{array}{rl}& bel(x_3=open)\\ & =P(x_3=open|x_0,z_1=0.5m,z_2=0.5m,u_3)\\ & =\eta \sum _{x_2}P(x_3|x_2,u_3)bel(x_2)\\ & =\eta (P(x_3|x_2=open,u_3)P(x_2=open)+P(x_3|\neg x_2,u_3)P(\neg x_2))\\ & =\eta \ast (0.1\ast 0.8+0\ast 0.2)=0.08\eta \end{array}$$
$$\begin{array}{rl}& bel(x_3=closed)\\ & =P(x_3=closed|x_0,z_1=0.5m,z_2=0.5m,u_3)\\ & =\eta \sum _{x_2}P(x_3|x_2,u_3)bel(x_2)\\ & =\eta (P(x_3|x_2=open,u_3)P(x_2=open)+P(x_3|\neg x_2,u_3)P(\neg x_2))\\ & =\eta \ast (0.9\ast 0.8+1\ast 0.2)=0.92\eta \end{array}$$
$$\begin{gathered} 0.08\eta +0.92\eta =\eta =1 \\ bel(x_2=open)=0.08\eta =0.08 \end{gathered}$$
注意这一部分，是只有动作而没有观测，所以只需要计算先验部分即可。

贝叶斯的缺点

可以看到，每一次添加新的动作或者观测的时候，概率都会发生改变，如果事件的可能情况很多，则需要计算很多次，特别的，如果是连续的概率，则可能发生的情况会有无穷多种，此时是不可能计算所有情况的。
但是，只要我们做一些假设，那么情况就会不一样了，例如

1)状态转移概率$P(x_k|u_k,x_{k-1})$必须是带有随机高斯噪声的参数的线性函数，即运动方程必须是线性的，且上一个状态也是高斯分布

$$x_k=A_k{x}_{k-1}+u_k+w_k{x}_{k-1}\sim N(x_{k-1},P_{k-1})w_k\sim N(0,R)$$

2)测量概率$P(z_k|x_k)$也与带有高斯噪声的自变量呈线性关系，即观测方程也是线性的

$$z_k=C_k{x}_k+v_k{x}_k\sim N(x_k,P_k)v_k\sim N(0,Q)$$

3)结合第一条当k=1,的时候,也必须符合高斯分布

$$x_0\sim N(x_0,P_0)$$
添加了上面的三个假设，那么可以证明，无论在什么时候$bel(x_k)$都是符合高斯分布的。接下来的推导按照《slam十四讲里》的推导,这样会和贝叶斯滤波的步骤对不上，如果完全按照贝叶斯滤波的那一套来，过程比较复杂，可以参考书《概率机器人》，也有博客细说kalman滤波。博客里面一些比较麻烦的推导没有写进来，如果感兴趣就直接看书吧，书里很全面，就是太复杂了。

卡尔曼滤波

先说一下，$\overline{bel}(x_k)=P(x_k|z_{1:k-1},u_{1:k},x_0)$和$P(x_k|x_{k-1},u_k)$是不一样的，虽然我们前面做了假设说$x_{k-1}$已经包含了k-1时刻和之前的所有信息$z_{1:k-1},u_{1:k-1},x_0$,但是这并不等价于$x_{k-1}$和前面的信息是等价的，事实上，应该是$x_{k-1}$在过去所有信息的影响下的所有可能的值都加上，才和过去所有的信息是等价，这一问题其实在推导的过程中也是已经出现了的
$$\overline{bel}(x_k)=\int P(x_k|x_{k-1},u_k)bel(x_{k-1})d{x}_{k-1}$$
也就是把$x_{k-1}$加进条件里的话，就是假设$x_{k-1}$已经发生了，此时的$x_{k-1}$已经是个确定的状态了，而不是代表一个概率密度。《概率机器人》里面是把$x_{k-1}$当成了一个确定的状态，直接利用代进$\overline{bel}(x_k)=\int P(x_k|x_{k-1},u_k)bel(x_{k-1})d{x}_{k-1}$表达式里，直接计算积分推导出$\overline{bel}(x_k)$，而《slam十四讲》里是直接把$x_{k-1}$当成了一个概率分布，而整个概率分布的就包含了过去的所有信息。

我觉得《概率机器人》里面的推导是比较直接的，逻辑比较好理解，和贝叶斯滤波一步步对应起来求解就好了，但是数学部分比较难看懂（例如积分怎么求），而《slam十四讲》里面的推导比较容易看懂（数学部分）。

卡尔曼滤波的推导

先给出一个成立的例子

考虑随机变量$x\sim N({\mu }_x,{\Sigma }_{xx})$,另一个变量y满足$$y=Ax+b+w$$其中 A,b 为线性变量的系数矩阵和偏移量， w 为噪声项，为零均值的高斯分布： w ∼N(0,R)。我们来看 y 的分布。根据前面的介绍，可以推出
$$p(y)=N(A{\mu }_x+b,A{\Sigma }_{xx}AT+R)$$

已知$$x_k=A_k{x}_{k-1}+u_k+w_k{x}_{k-1}\sim N(x_{k-1},P_{k-1})w_k\sim N(0,R)$$
求$x_k$的概率分布，直接代进上面的例子，直接就可以得到先验部分
$$\overline{bel}(x_k)=P(x_k|z_{1:k-1},u_{1:k},x_0)\sim N(A_k{x}_{k-1}+u_k,A_k{P}_{k-1}{A}_k^T+R)$$
同时记$$\begin{gathered} {\overline{x}}_k=A_k{x}_{k-1}+u_k \\ {\overline{P}}_k=A_k{P}_{k-1}{A}_k^T+R \end{gathered}$$
则$$\overline{bel}(x_k)=P(x_k|z_{1:k-1},u_{1:k},x_0)\sim N({\overline{x}}_k,{\overline{P}}_k)$$
接下来，通过观测方程，计算似然部分
$$z_k=C_k{x}_k+v_k{x}_k\sim N(x_k,P_k)v_k\sim N(0,Q)$$
似然$P(z_k|x_k)$里面，$x_k$是已知的，所以此时的$x_k$是一个确定的值，而不是一个概率，可以得到
$$P(z_k|x_k)\sim N(C_k{x}_k,Q)$$
接下来是用了点小技巧，就是我们已知结果会是一个高斯函数，我们直接设结果为$$bel(x_k)\sim N({\hat{x}}_k,{\hat{P}}_k)$$
则带进贝叶斯滤波器可以得到
$$N({\hat{x}}_k,{\hat{P}}_k)=\eta N(C_k{x}_k,Q)\cdot N({\overline{x}}_k,{\overline{P}}_k)$$
接下来只要得到解这个式子然后通过对比指数部分，就可以得到${\hat{x}}_k,{\hat{P}}_k$,具体过程直接《slam十四讲》,接下来直接截图书里的内容（因为公式太多了，而且基本是照书里打）

可以得到卡尔曼滤波的迭代公式
预测部分
$$\overline{bel}(x_k)\{\begin{array}{l}{\overline{x}}_k=A_k{x}_{k-1}+u_k\\ {\overline{P}}_k=A_k{P}_{k-1}{A}_k^T+R\end{array}$$
卡尔曼增益
$$K={\overline{P}}_k{C}_k^T(C_k{\overline{P}}_k{C}_k^T+Q{)}^{-1}$$
后验部分
$$bel(x_k)\{\begin{array}{l}{\hat{x}}_k={\overline{x}}_k+K(z_k-C_k{\overline{x}}_k)\\ {\hat{P}}_k=(I-K{C}_k){\overline{P}}_k\end{array}$$
到这里就成功的推导出了卡尔曼滤波了

opencv实现例子

#include 
#include 
#include 
#include 
using namespace std;
using namespace cv;
void drawLine(Mat src, vector<Point2f> p, cv::Scalar sc);
int main()
{
    //创建一堆点，没有控制方程的，即X(K)=A(K-1)+b*u+P;
    vector<Point2f> vpt(100);
    for (int i = 0; i < 100; i++) {
        vpt[i].x = i * 7 + 50;
        vpt[i].y = vpt[i].x;
    }
    vector<Point2f> vpt_gauss(100);
    RNG rng;
    for (int i = 0; i < 100; i++) {
        vpt_gauss[i] = vpt[i] + Point2f(rng.gaussian(10), rng.gaussian(10));
    }

    const int stateNum = 4; //状态值4×1向量(x,y,△x,△y)
    const int measureNum = 2; //测量值2×1向量(x,y)
    KalmanFilter KF(stateNum, measureNum, 0);

    KF.transitionMatrix = (Mat_<float>(4, 4) << 1, 0, 1,0,
												0,1,0,1,
												0,0,1,0,
												0,0,0,1); //转移矩阵A
    KF.measurementMatrix=(Mat_<float>(2,4)<<1,0,0,0,
											0,1,0,0);//测量矩阵H
    setIdentity(KF.processNoiseCov, Scalar::all(1e-5)); //系统噪声方差矩阵R w
    setIdentity(KF.measurementNoiseCov, Scalar::all(1e-1)); //测量噪声方差矩阵Q v
    setIdentity(KF.errorCovPost, Scalar::all(1)); //后验错误估计协方差矩阵P w
    KF.statePost = (Mat_<float>(4, 1) << 50, 50,7,7);
    cout << KF.statePost << std::endl;
    Mat measurement = Mat::zeros(measureNum, 1, CV_32F); //初始测量值x'(0)，因为后面要更新这个值，所以必须先定义
    vector<Point2f> vpt_kal(100);
    for (int i = 0; i < 100; i++) {
        measurement.at<float>(0, 0) = vpt_gauss[i].x;
        measurement.at<float>(1, 0) = vpt_gauss[i].y;

        KF.predict();
        Mat res = KF.correct(measurement);
        vpt_kal[i].x = res.at<float>(0, 0);
        vpt_kal[i].y = res.at<float>(1, 0);
		cout<<res<<endl;

    }
    Mat drawBoard(800, 800, CV_8UC3);
    drawLine(drawBoard, vpt, Scalar(255, 0, 0));
    drawLine(drawBoard, vpt_gauss, Scalar(0, 255, 0));
    drawLine(drawBoard, vpt_kal, Scalar(0, 0, 255));

    while (1) {
        imshow("kalman", drawBoard);
        waitKey(0);
    }
    return 0;
}
void drawLine(Mat src, vector<Point2f> p, cv::Scalar sc)
{

    for (int i = 0; i < p.size() - 1; i++) {
        line(src, p[i], p[i + 1], sc);
    }
    for (int i = 0; i < p.size(); i++) {
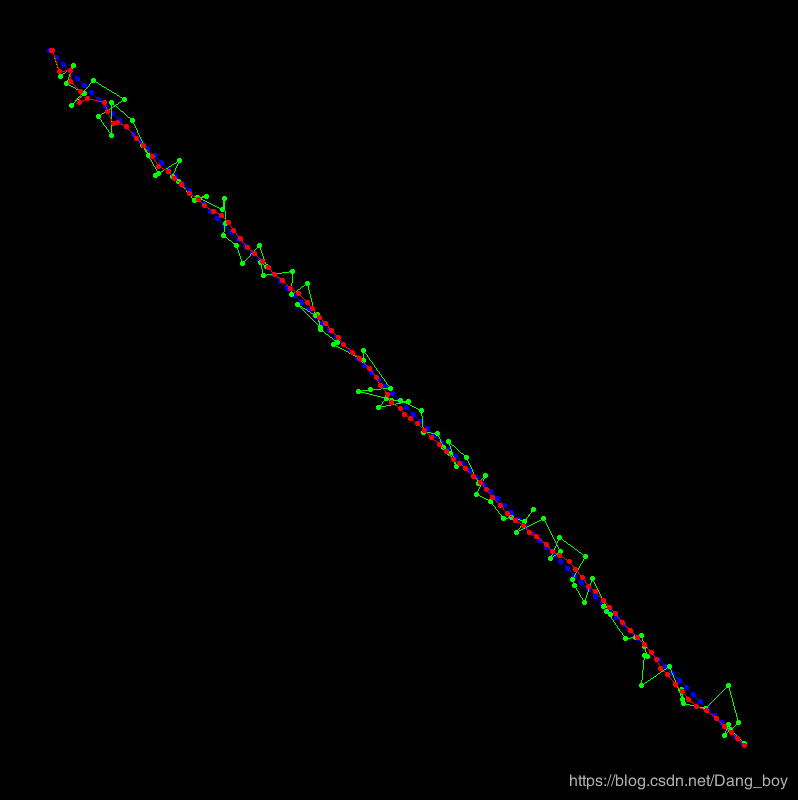
        circle(src, p[i], 1, sc, 2);
    }
}

蓝色的线是不带噪声的
绿色的线是带噪声的
红色的线是用待噪声的数据滤波出来的结果

可以看到红色的线一开始波动比较大，到最后基本稳定在蓝色的线周围小幅度的摆动，比起绿色的线，效果已经好了很多了。
参考资料:
《slam十四讲》
《概率机器人》
（一）. 细说贝叶斯滤波：Bayes filters
（二）. 细说Kalman滤波：The Kalman Filter