多项式乘法(FFT)详解
本文只探讨多项式乘法(FFT)在信息学中的应用
如有错误或不明欢迎指出或提问,在此不胜感激
多项式
1. 系数表示法
一般应用最广泛的表示方式
用A(x)表示一个x-1次多项式,a[i]为 xi x i 的系数,则A(x)= ∑n−10 ∑ 0 n − 1 a[i] * xi x i
仅利用这种方式求多项式乘法复杂度为O( n2 n 2 ),不够优秀
2.点值表示法
将n个互不相同的值 x0 x 0 … xn−1 x n − 1 带入多项式,可以得到
对于一个n-1次多项式,可以被n个点所唯一对应.
因而对于A(x)*B(x),只需要得知A的2n个点值和对应B的2n个点值即可O(n)求出多项式的乘积
然而得知这些点值的复杂度依然在平方级别,达不到要求
考虑优化
先引一些要用到的名词
复数
复数即为表示成a+bi的数,其中i为-1的平方根
表示:
可以通过平面直角坐标系上的一条向量(0,0)到(x,y)表示x+yi
其中x轴为实数轴,y轴为虚数轴
运算:
复数运算符合四则运算,即:
(a+bi) + (c+di) = (a+c) + (b+d)i;
(a+bi) * (c+di) = ac + adi + bci - bd i2 i 2 =(ac - bd) + (bc + ad)i
几何意义:
定义模长为向量长度,幅角为从x轴正半轴逆时针转动到向量的角
复数相加等同于向量加法
复数相乘,模长相乘,幅角相加
//建议complex类手写,速度优于STL
单位根
以下默认n为 2x 2 x 且x为非负整数
在复数平面,以原点为圆心,以1为半径作圆
以x轴正半轴到其与原交点(0,0)到(1,0)的这条向量为起点n等分圆,圆心到每个n等分点的向量均称为n次单位根
对于一个单位根,其标号为幅角/(360°/n),特别的,(0,0)到(1,0)的向量标号为0
以下用 wkn w n k 表示标号为k的n次单位根
单位根的性质
1. wkn w n k = cos( 2πn 2 π n )k + sin( 2πn 2 π n )ki
证明:欧拉公式
2. wkn w n k = w2k2n w 2 n 2 k
证明:带入式1,等价于分子分母同乘2,
3. wkn w n k * wkn w n k = w2kn w n 2 k
证明:根据(复数相乘,模长相乘,幅角相加)
又因为模长均为1,所以相当于只把转动角度乘2
4. wk+n2n w n k + n 2 = - wkn w n k
证明: wk+n2n w n k + n 2 相当于在 wkn w n k 的基础上逆时针方向再旋转180° (复数相乘,模长相乘,幅角相加)
因而等价于取负
设多项式A(x)的系数为 a0 a 0 … an−1 a n − 1
则A(x) = a0 a 0 + a1 a 1 * x + a2 a 2 * x2 x 2 + a3 a 3 * x3 x 3 + a4 a 4 * x4 x 4 + … + an−2 a n − 2 * xn−2 x n − 2 + an−1 a n − 1 * xn−1 x n − 1
按下标奇偶性分成两组,在这里设
A0(x) = a0 a 0 + a2 a 2 * x x + a4 a 4 * x2 x 2 + … + an−2 a n − 2 * xn−22 x n − 2 2
A1(x) = a1 a 1 + a3 a 3 * x x + a5 a 5 * x2 x 2 + … + an−1 a n − 1 * xn−22 x n − 2 2
显然得到A(x) = A0( x2 x 2 ) + xA1( x2 x 2 )
我们代单位根 wkn w n k (0<=k< n2 n 2 )入式得
A( wkn w n k )=A0( w2kn w n 2 k )+ wkn w n k A1( w2kn w n 2 k )//性质3
同理代 wk+n2n w n k + n 2 入式得
A( wk+n2n w n k + n 2 )=A0( w2k+nn w n 2 k + n )+ wk+n2n w n k + n 2 A1( w2k+nn w n 2 k + n )
= A0( w2kn w n 2 k ) - wkn w n k * A1( w2kn w n 2 k )//性质4&& wnn w n n =1
容易发现上下两式只有常数项的符号不同
因而只需求前一般即可得到后一般
递归形式程序结构:
对于长度为n的A(x)
分割成长度为 n2 n 2 的A0(x)和A1(x)
求A0(x)和A1(x)
通过A0(x)和A1(x)计算带入 wkn w n k (0<=k< n2 n 2 )时的值
变号计算代 wk+n2n w n k + n 2 入式的值
我们可以用数组A[i]表示某一多项式(不一定是初始多项式)代入 win w n i }时的值
由于许多奥妙重重的性质,我们不需要对于每个多项式都维护整个数组A,只需要维护它需要返回的值即可
绘图可得,当某一多项式递归到只有一项的时候,要返回的一定只是 w0n w n 0 (1),即直接返回原多项式该项系数即可
递归代码:
void FFT(const int lim,cp *A)//cp即为complex类型,lim为2^n的整型
{
if(lim==1)return;//直接返回对应常数项
cp A0[lim>>1],A1[lim>>1];
for(rt i=0;i2)A0[i>>1]=A[i],A1[i>>1]=A[i+1];
FFT(lim>>1,A0,fla);FFT(lim>>1,A1,fla);//递归求解
cp w={cos(PI*2.0/lim),sin(PI*2.0/lim)},k={1,0};//w为1号单位根
for(rt i=0;i>1;i++,k=k*w)//k即为第i个单位根
{
A[i]=A0[i]+k*A1[i];//A0,A1数组中的i号本相当于A数组中的2i号,乘2再除2后相当于没有
A[i+(lim>>1)]=A0[i]-k*A1[i];
}
} 逆变换
以上求得的均为点值表示法的结果
需要将其转回系数表示法
实际操作相当于再进行FFT时单位根逆向(顺时针)计算
递归全代码
#include2)A1[i>>1]=A[i],A2[i>>1]=A[i+1];
FFT(lim>>1,A1,fla);FFT(lim>>1,A2,fla);
cp w={cos(PI*2.0/lim),sin(PI*2.0/lim)*fla},k={1,0};
for(rt i=0;i>1;i++,k=k*w)
{
A[i]=A1[i]+k*A2[i];
A[i+(lim>>1)]=A1[i]-k*A2[i];
}
}
int main()
{
n=r;m=r;
for(rt i=0;i<=n;i++)a[i].x=r,a[i].y=0;
for(rt i=0;i<=m;i++)b[i].x=r,b[i].y=0;
int limit=1;while(limit<=n+m)limit<<=1;//将多项式长度凑到2^n
FFT(limit,a,1);FFT(limit,b,1);
for(rt i=0;i<=limit;i++)a[i]=a[i]*b[i];//a为点值表示的多项式
FFT(limit,a,-1);//逆变换
for(rt i=0;i<=n+m;i++)write(a[i].x/limit+0.5),putchar(' ');
//因为有limit个单位根因而答案需要除limit,0.5是四舍五入
return 0;
} 问题:常数巨大
解决方案:改成非递归(迭代)形式
观察下图
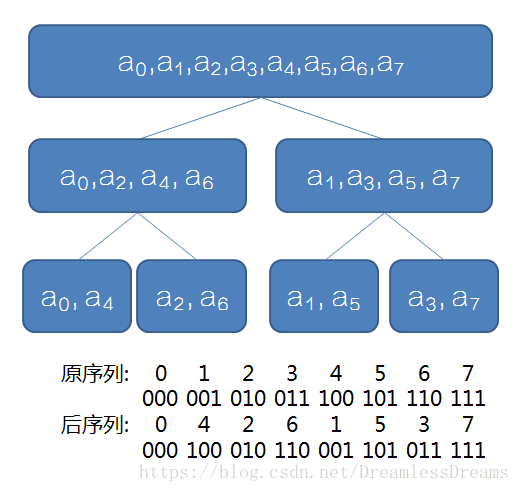
发现底层序列的值相当于原序列的值的二进制反转
因而我们可以预处理底层的值然后迭代向上推
如何预处理
1.x为偶数
x=(x>>1)<<1;
在反转序列中reverse[x]=reverse[x>>1]>>1;
2.x为奇数
相当于x-1的结果再在最高位补1
这样我们得到底层结果之后,一层一层向上迭代合并即可
迭代代码:
#includeif(i//得到底层数列
for(rt i=1;i1)//i表示当前层的下面每个区间大小为i
{
cp w={cos(PI/i),fla*sin(PI/i)};//本应为2PI/2i
for(rt j=0;j1))//j为当前层的每个起始端点
{
cp K={1,0};
for(rt k=0;k//k枚举当前层的j所在区间的元素
{
const cp x=A[j+k],y=K*A[j+k+i];//求解,如果对递归理解深刻应该能理解这段
A[j+k]=x+y;
A[j+k+i]=x-y;
}
}
}
}
int main()
{
n=r;m=r;
for(rt i=0;i<=n;i++)a[i].x=r;
for(rt i=0;i<=m;i++)b[i].x=r;
lim=1;while(lim<=n+m)lim*=2,li++;
for(rt i=0;i>1]>>1)+((i&1)<<(li-1));
FFT(a,1);FFT(b,1);
for(rt i=0;i1);
for(rt i=0;i<=(n+m);i++)printf("%d ",(int)(a[i].x/lim+0.5));
return 0;
}
