超详细易懂FFT(快速傅里叶变换)及代码实现
前言
昨天学了一晚上,终于搞懂了FFT。希望能写一篇清楚易懂的题解分享给大家,也进一步加深自己的理解。
FFT算是数论中比较重要的东西,听起来就很高深的亚子。但其实学会了(哪怕并不能完全理解),会实现代码,并知道怎么灵活运用 (背板子) 就行。接下来进入正题。
定义
FFT(Fast Fourier Transformation),中文名快速傅里叶变换,是离散傅氏变换的快速算法,它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
而在信奥中,一般用来加速多项式乘法。
朴素高精度乘法的时间为 O ( n 2 ) O(n^2) O(n2),但FFT能将时间复杂度降到 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
学习FFT之前,需要了解一些有关复数和多项式的知识。
有关知识
多项式的两种表示方法
系数表示法
F [ x ] = y = a 0 x 0 + a 1 x 1 + a 2 x 2 + . . . . . . a n x n F[x]=y=a_0x^0+a_1x^1+a_2x^2+......a_nx^n F[x]=y=a0x0+a1x1+a2x2+......anxn
{ a 0 , a 1 , a 2 , . . . , a n a_0,a_1,a_2,...,a_n a0,a1,a2,...,an} 是这个多项式每一项的系数,所以这是多项式的系数表示法
点值表示法
在函数图像中, F [ x ] F[x] F[x]这个多项式可以被n个点唯一确定,即代入n个点作为 x x x,分别解出对应的 y y y,得到n个式子。把这n条式子联立起来成为一个有n条方程的n元方程组,每一项的系数都可以解出来.(可类比二元一次方程)
也就是说,使用{ ( x 0 , f [ x 0 ] ) (x_0,f[x_0]) (x0,f[x0]), ( x 1 , f [ x 1 ] ) (x_1,f[x_1]) (x1,f[x1]),…, ( x n , f [ x n ] ) (x_n,f[x_n]) (xn,f[xn])}就可以完整描述出这个多项式,这就是 多项式的点值表示法
多项式相乘
设两个多项式分别为 f ( x ) f(x) f(x), g ( x ) g(x) g(x),我们要把这两个多项式相乘 (即求卷积)。
如果用系数表示法:
我们要枚举 f f f的每一位的系数与 g g g的每一位的系数相乘,多项式乘法时间复杂度 O ( n 2 ) O(n^2) O(n2),这也是我们所熟知的高精度乘法的原理。
如果用点值表示法:
f [ x ] f[x] f[x]={ ( x 0 , f [ x 0 ] ) (x_0,f[x_0]) (x0,f[x0]), ( x 1 , f [ x 1 ] ) (x_1,f[x_1]) (x1,f[x1]),…, ( x n , f [ x n ] ) (x_n,f[x_n]) (xn,f[xn])}
g [ x ] g[x] g[x]={ ( x 0 , g [ x 0 ] ) (x_0,g[x_0]) (x0,g[x0]), ( x 1 , g [ x 1 ] ) (x_1,g[x_1]) (x1,g[x1]),…, ( x n , g [ x n ] ) (x_n,g[x_n]) (xn,g[xn])}
f [ x ] ∗ g [ x ] f[x]*g[x] f[x]∗g[x]={ ( x 0 , f [ x 0 ] ∗ g [ x 0 ] ) (x_0,f[x_0]*g[x_0]) (x0,f[x0]∗g[x0]), ( x 1 , f [ x 1 ] ∗ g [ x 1 ] ) (x_1,f[x_1]*g[x_1]) (x1,f[x1]∗g[x1]),…, ( x n , f [ x n ] ∗ g [ x n ] ) (x_n,f[x_n]*g[x_n]) (xn,f[xn]∗g[xn])}
我们可以发现,如果两个多项式取相同的 x x x,得到不同的 y y y值,那么只需要 y y y值对应相乘就可以了!
复杂度只有枚举 x x x的 O ( n ) O(n) O(n)
那么问题转换为将多项式系数表示法转化成点值表示法。
朴素系数转点值的算法叫DFT(离散傅里叶变换),优化后为FFT(快速傅里叶变换),点值转系数的算法叫IDFT(离散傅里叶逆变换),优化后为IFFT(快速傅里叶逆变换)。之后我会分别介绍。
卷积
其实不理解卷积也没关系,但这里顺便提一下,可以跳过的
卷积与傅里叶变换有着密切的关系。利用一点性质,即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换,能使傅里叶分析中许多问题的处理得到简化。
F ( g ( x ) ∗ f ( x ) ) = F ( g ( x ) ) F ( f ( x ) ) F(g(x)*f(x)) = F(g(x))F(f(x)) F(g(x)∗f(x))=F(g(x))F(f(x))
其中F表示的是傅里叶变换
复数
高中数学会详细讲解,知道的可以跳过这一部分,没学过也没关系,看以下内容应该能很清楚的理解。
1.定义
数集拓展到实数范围内,仍有些运算无法进行。比如判别式小于0的一元二次方程仍无解,因此将数集再次扩充,达到复数范围。
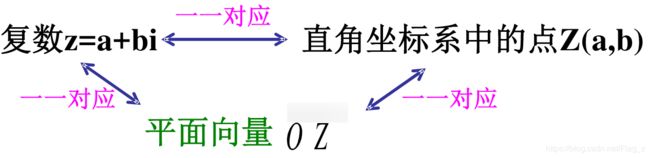
复数 z z z被定义为二元有序实数对 ( a , b ) (a,b) (a,b),记为 z = a + b i z=a+bi z=a+bi,这里 a a a和 b b b是实数,规定 i i i是虚数单位。 ( i 2 = − 1 i^2=-1 i2=−1 即 i = − 1 i=\sqrt{-1} i=−1)
对于复数 z = a + b i z=a+bi z=a+bi。实数 a a a称为复数z的实部(real part),记作 r e z = a rez=a rez=a.实数 b b b称为复数z的虚部(imaginary part)记作 Imz=b.
当虚部等于零时,这个复数可以视为实数。
即当 b = 0 b=0 b=0时, z = a z=a z=a,这时复数成为实数;当且仅当 a = b = 0 a=b=0 a=b=0时,它是实数0;
当z的虚部不等于零时,实部等于零时,常称z为纯虚数。
即当 a = 0 a=0 a=0且 b ≠ 0 b≠0 b̸=0时, z = b i z=bi z=bi,我们就将其称为纯虚数。
将复数的实部与虚部的平方和的正的平方根的值称为该复数的模,记作 ∣ z ∣ ∣z∣ ∣z∣。
即对于复数z=a+bi,它的模为 ∣ z ∣ = ( a 2 + b 2 ) ∣z∣=\sqrt{(a^2+b^2)} ∣z∣=(a2+b2)
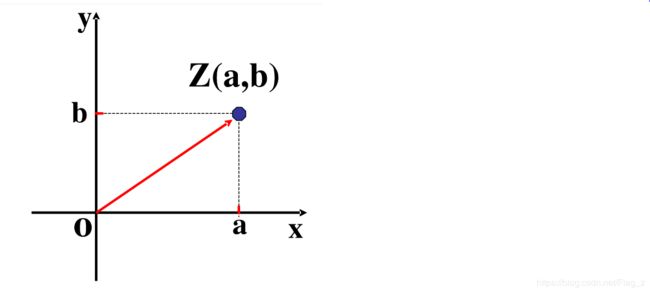
2.复数的几何意义
3.运算法则
加法法则: ( a + b i ) + ( c + d i ) = ( a + c ) + ( b + d ) i ; (a+bi)+(c+di)=(a+c)+(b+d)i; (a+bi)+(c+di)=(a+c)+(b+d)i;
减法法则: ( a + b i ) − ( c + d i ) = ( a − c ) + ( b − d ) i ; (a+bi)-(c+di)=(a-c)+(b-d)i; (a+bi)−(c+di)=(a−c)+(b−d)i;
注:复数加减满足平行四边形法则:
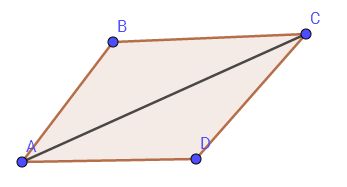
乘法法则: ( a + b i ) ⋅ ( c + d i ) = ( a c − b d ) + ( b c + a d ) i (a+bi)·(c+di)=(ac-bd)+(bc+ad)i (a+bi)⋅(c+di)=(ac−bd)+(bc+ad)i
复数相乘一个重要法则:模长相乘,幅角相加。(这个定理很重要)
模长:这个向量的模长,即这个点到原点的距离。(不懂的可再看下向量的几何意义)。
幅角: 从原点出发、指向x轴正半轴的射线绕原点逆时针旋转至过这个点所经过的角。
在极坐标(可看成平面直角坐标系)下,复数可用模长r与幅角θ表示为 ( r , θ ) (r,θ) (r,θ)。对于复数 a + b i a+bi a+bi, r = ( a ² + b ² ) r=\sqrt{(a²+b²)} r=(a²+b²), θ = a r c t a n ( b / a ) θ=arctan(b/a) θ=arctan(b/a)。此时,复数相乘表现为模长相乘,幅角相加。
除法法则: ( a + b i ) ÷ ( c + d i ) = [ ( a c + b d ) / ( c ² + d ² ) ] + [ ( b c − a d ) / ( c ² + d ² ) ] i (a+bi)÷(c+di)=[(ac+bd)/(c²+d²)]+[(bc-ad)/(c²+d²)]i (a+bi)÷(c+di)=[(ac+bd)/(c²+d²)]+[(bc−ad)/(c²+d²)]i
4. 共轭复数
一个复数 z = a + b i z=a+bi z=a+bi的共轭复数为 a − b i a−bi a−bi(实部不变,虚部取反),记为 z ‾ = a − b i \overline{z}=a-bi z=a−bi
当复数模为1时(即|z|=1),与共轭复数互为倒数
证明: z ∗ z ‾ = a 2 − b 2 ∗ i 2 = a 2 + b 2 = ∣ z ∣ 2 = 1 z*\overline{z}=a^2-b^2*i^2=a^2+b^2=|z|^2=1 z∗z=a2−b2∗i2=a2+b2=∣z∣2=1
FFT加速多项式乘法
由于多项式乘法用点值表示比用系数表示快的多,所以我们先要将系数表示法转化成点值表示法相乘,再将结果的点值表示法转化为系数表示法的过程。
第一个过程叫做FFT(快速傅里叶变换),第二个过程叫IFFT(快速傅里叶逆变换)
在讲这两个过程之前,首先了解一个概念:
单位根
复数 ω \omega ω满足 ω n = 1 \omega^n=1 ωn=1,称 ω \omega ω是n次单位根
怎么找单位根?
单位圆:圆心为原点、1为半径的圆
把单位圆n等分,取这n个点(或点表示的向量)所表示的复数(即分别以这n个点的横坐标为实部、纵坐标为虚部,所构成的虚数),即为n次单位根。
下图包含了当n=8时,所有的8次单位根,分别记为 ω 8 1 , ω 8 2 . . . . . , ω 8 8 \omega_8^1,\omega_8^2.....,\omega_8^8 ω81,ω82.....,ω88
(图中圆的半径是1,w表示 ω \omega ω,且下标8已省略)
图是我自己画的,可能有点丑QWQ
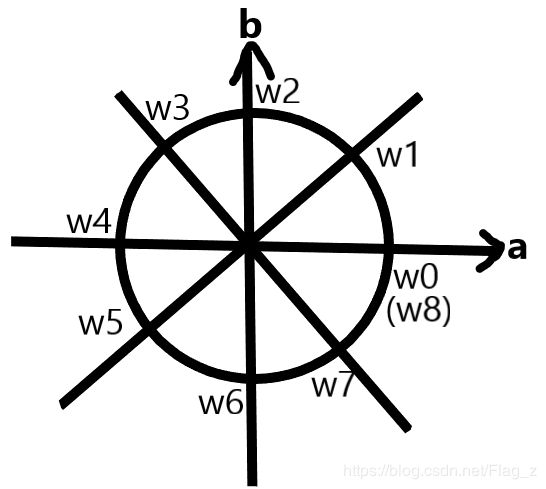
由此我们知道如何找单位根啦
从点(1,0)开始(即 ω n 1 \omega_n^1 ωn1),逆时针将这n个点从0开始编号,第k个点对应的虚数记作 ω n k \omega_n^k ωnk
由复数相乘法则:模长相乘幅角相加 可得:
( ω n 1 ) k = ω n k (\omega_n^1)^k=\omega_n^k (ωn1)k=ωnk
根据每个复数的幅角,可以计算出所对应的点/向量。 ω n k \omega_n^k ωnk 对应的点/向量是 ( c o s k n 2 π , s i n k n 2 π ) (cos\frac kn2π,sin\frac kn2π) (cosnk2π,sinnk2π),即为复数 c o s k n 2 π + i ∗ s i n k n 2 π cos\frac kn2π+i *sin\frac kn2π cosnk2π+i∗sinnk2π
单位根的性质
建议记住,因为对之后的分析很重要!!
1. ω n k = ω 2 n 2 k \omega_n^k=\omega_{2n}^{2k} ωnk=ω2n2k
2. ω n k = − ω n k + n 2 \omega_n^k=-\omega_{n}^{k+\frac n 2} ωnk=−ωnk+2n
3. ω n 0 = ω n n = 1 \omega_n^0=\omega_{n}^n=1 ωn0=ωnn=1
至于怎么证明,就是复数相乘时模长相乘幅角相加的原则。或者你直接观察图也可以很显然的得出结论。
DFT(离散傅里叶变换)
对于任意多项式系数表示转点值表示,例如 F [ x ] = y = a 0 x 0 + a 1 x 1 + a 2 x 2 + . . . . . . + a n x n F[x]=y=a_0x^0+a_1x^1+a_2x^2+......+a_nx^n F[x]=y=a0x0+a1x1+a2x2+......+anxn ,可以随便取任意n个 x x x值代入计算,但这样时间复杂度是 O ( n 2 ) O(n^2) O(n2)
所以伟大数学家傅里叶取了一些特殊的点代入,从而进行优化。
他规定了点值表示中的 n n n个 x x x为 n n n个模长为1的复数。这 n n n个复数不是随机的,而是单位根。
把上述的n个复数(单位根) ω n 0 , ω n 1 . . . . . , ω n n − 1 \omega_n^0,\omega_n^1.....,\omega_n^{n-1} ωn0,ωn1.....,ωnn−1代入多项式,能得到一种特殊的点值表示,这种点值表示就叫DFT(离散傅里叶变换)。
FFT(快速傅里叶变换)
虽然DFT能把多项式转换成点值但它仍然是暴力代入 n n n个数,复杂度仍然是O(n2),所以它只是快速傅里叶变换的朴素版。
所以我们要考虑利用单位根的性质,加速我们的运算,得到FFT(快速傅里叶变换)
对于多项式 A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a n − 1 x n − 1 A(x)=a_0+a_1x+a_2x^2+...+a_{n−1}x^{n−1} A(x)=a0+a1x+a2x2+...+an−1xn−1
将A(x)的每一项按照下标的奇偶分成两部分:
A ( x ) = a 0 + a 2 x 2 + . . . + a n − 2 x n − 2 + x ∗ ( a 1 + a 3 x 2 + . . . + a n − 1 x n − 2 ) A(x)=a_0+a_2x^2+...+a_{n−2}x^{n−2}+x*(a_1+a_3x^2+...+a_{n−1}x^{n−2}) A(x)=a0+a2x2+...+an−2xn−2+x∗(a1+a3x2+...+an−1xn−2)
设两个多项式 A 0 ( x ) A_0(x) A0(x)和 A 1 ( x ) A_1(x) A1(x),令:
A 0 ( x ) = a 0 x 0 + a 2 x 1 + . . . + a n − 1 x n / 2 − 1 A_0(x)=a_0x^0+a_2x^1+...+a_{n-1}x^{n/2-1} A0(x)=a0x0+a2x1+...+an−1xn/2−1
A 1 ( x ) = a 1 x 0 + a 3 x 1 + . . . + a n − 2 x n / 2 − 1 A_1(x)=a_1x^0+a_3x^1+...+a_{n-2}x^{n/2-1} A1(x)=a1x0+a3x1+...+an−2xn/2−1
显然, A ( x ) = A 0 ( x 2 ) + x ∗ A 1 ( x 2 ) A(x)=A_0(x^2)+x*A_1(x^2) A(x)=A0(x2)+x∗A1(x2)
假设 k < n k<n k<n,代入 x = ω n k x=ω_n^k x=ωnk(n次单位根):
A ( ω n k ) A(\omega_n^k) A(ωnk) = A 0 ( ω n 2 k ) + ω n k ∗ A 1 ( ω n 2 k ) =A_0(\omega_n^{2k})+\omega_n^{k}*A_1(\omega_n^{2k}) =A0(ωn2k)+ωnk∗A1(ωn2k)
= A 0 ( ω n 2 k ) + ω n k ∗ A 1 ( ω n 2 k ) =A_0(\omega_\frac n2^{k})+\omega_n^{k}*A_1(\omega_\frac n 2^{k}) =A0(ω2nk)+ωnk∗A1(ω2nk)
A ( ω n k + n 2 ) = A 0 ( ω n 2 k + n ) + ω n k + n 2 ∗ A 1 ( ω n 2 k + n ) A(\omega_n^{k+\frac n 2})=A_0(\omega_n^{2k+n})+\omega_n^{k+\frac n 2}*A_1(\omega_n^{2k+n}) A(ωnk+2n)=A0(ωn2k+n)+ωnk+2n∗A1(ωn2k+n)
= A 0 ( ω n 2 k ) − ω n k ∗ A 1 ( ω n 2 k ) =A_0(\omega_\frac n2^{k})-\omega_n^{k}*A_1(\omega_\frac n 2^{k}) =A0(ω2nk)−ωnk∗A1(ω2nk)
考虑A1(x)和A2(x)分别在 ( ω n 2 1 , ω n 2 2 , ω n 2 3 , . . . , ω n 2 n 2 − 1 ) (\omega_\frac n 2^{1},\omega_\frac n 2^{2},\omega_\frac n 2^{3},...,\omega_\frac n 2^{\frac n 2-1}) (ω2n1,ω2n2,ω2n3,...,ω2n2n−1)的点值表示已经求出,就可以O(n)求出A(x)在 ( ω n 1 , ω n 2 , ω n 3 , . . . , ω n n − 1 ) (\omega_n ^{1},\omega_n ^{2},\omega_n ^{3},...,\omega_n ^{n-1}) (ωn1,ωn2,ωn3,...,ωnn−1)处的点值表示。这个操作叫蝴蝶变换
而A1(x)和A2(x)是规模缩小了一半的子问题,所以不断向下递归分治。当n=1的时候返回。
注:这个过程一定要求每层都可以分成两大小相等的部分,所以多项式最高次项一定是2的幂,不是的话直接在最高次项补零QAQ。
时间复杂度 O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)
IFFT(快速傅里叶逆变换)
我们已经将两个多项式从系数表示法转化成点值表示法相乘后,还要将结果从点值表示法转化为系数表示法,也就是IFFT(快速傅里叶逆变换)
首先思考一个问题,为什么要把 ω n k \omega_n^k ωnk(单位根)作为x代入?
当然是因为离散傅里叶变换特殊的性质,而这也和IFFT有关。
一个重要结论
把多项式A(x)的离散傅里叶变换结果作为另一个多项式B(x)的系数,取单位根的倒数即 ω n 0 , ω n − 1 . . . . . , ω n 1 − n \omega_n^0,\omega_n^{-1}.....,\omega_n^{1-n} ωn0,ωn−1.....,ωn1−n作为x代入B(x),得到的每个数再除以n,得到的是A(x)的各项系数,这就实现了傅里叶变换的逆变换了。相当于在FFT基础上再搞一次FFT。
证明(个人觉得写的非常清楚,不想看的跳过吧)~~
设 ( y 0 , y 1 , y 2 , . . . , y n − 1 ) (y_0,y_1,y_2,...,y_{n−1}) (y0,y1,y2,...,yn−1)为多项式
A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a n − 1 x n − 1 A(x)=a_0+a_1x+a_2x^2+...+a_{n−1}x^{n−1} A(x)=a0+a1x+a2x2+...+an−1xn−1的离散傅里叶变换。
设多项式 B ( x ) = y 0 + y 1 x + y 2 x 2 + . . . + y n − 1 x n − 1 B(x)=y_0+y_1x+y_2x^2+...+y_{n−1}x^{n−1} B(x)=y0+y1x+y2x2+...+yn−1xn−1
把离散傅里叶变换的 ω n 0 , ω n 1 . . . . . , ω n n − 1 \omega_n^0,\omega_n^1.....,\omega_n^{n-1} ωn0,ωn1.....,ωnn−1这n个单位根的倒数,即 ω n 0 , ω n − 1 . . . . . , ω n 1 − n \omega_n^0,\omega_n^{-1}.....,\omega_n^{1-n} ωn0,ωn−1.....,ωn1−n作为x代入 B ( x ) B(x) B(x), 得到一个新的离散傅里叶变换 ( z 0 , z 1 , z 2 , . . . , z n − 1 ) (z_0,z_1,z_2,...,z{n−1}) (z0,z1,z2,...,zn−1)
z k z_k zk= ∑ i = 0 n − 1 y i ( ω n − k ) i \sum_{i=0}^{n−1}y_i(ω_n^{-k})^i ∑i=0n−1yi(ωn−k)i
= ∑ i = 0 n − 1 ( ∑ j = 0 n − 1 a j ∗ ( ω n i ) j ) ( ω n − k ) i \sum_{i=0}^{n−1}(\sum_{j=0}^{n-1}a_j*(\omega_n^i)^j)(ω_n^{-k})^i ∑i=0n−1(∑j=0n−1aj∗(ωni)j)(ωn−k)i
= ∑ j = 0 n − 1 a j ∗ ( ∑ i = 0 n − 1 ( ω n i ) j − k ) \sum_{j=0}^{n-1}a_j*(\sum_{i=0}^{n−1}(\omega_n^i)^{j-k}) ∑j=0n−1aj∗(∑i=0n−1(ωni)j−k)
当 j − k = 0 j−k=0 j−k=0时, ∑ i = 0 n − 1 ( ω n i ) j − k = n \sum_{i=0}^{n−1}(\omega_n^i)^{j-k}=n ∑i=0n−1(ωni)j−k=n
否则,通过等比数列求和可知:
∑ i = 0 n − 1 ( ω n i ) j − k \sum_{i=0}^{n−1}(\omega_n^i)^{j-k} ∑i=0n−1(ωni)j−k= ( ω n j − k ) n − 1 ω n j − k − 1 \frac{(ω_n^{j−k})^n-1}{ω_n^{j−k}-1} ωnj−k−1(ωnj−k)n−1= ( ω n n ) j − k − 1 ω n j − k − 1 \frac{(ω_n^{n})^{j-k}-1}{ω_n^{j−k}-1} ωnj−k−1(ωnn)j−k−1= 1 − 1 ω n j − k − 1 \frac{1-1}{ω_n^{j−k}-1} ωnj−k−11−1=0
(因为 ω n n \omega_n^n ωnn= ω n 0 \omega_n^0 ωn0=1)
所以
z k z_k zk= n ∗ a k n*a_k n∗ak
a k a_k ak= z k n \frac {z_k} n nzk ,得证。
怎么求单位根的倒数呢?
单位根的倒数其实就是它的共轭复数 。不明白的可以看看前面共轭复数的介绍
到现在你已经完全学会FFT了,但写递归还是可能会超时,所以我们需要优化
优化:迭代FFT
在进行FFT时,我们要把各个系数不断分组并放到两侧,一个系数原来的位置和最终的位置的规律如下。
初始位置: ω n 0 \omega_n^0 ωn0 ω n 1 \omega_n^1 ωn1 ω n 2 \omega_n^2 ωn2 ω n 3 \omega_n^3 ωn3 ω n 4 \omega_n^4 ωn4 ω n 5 \omega_n^5 ωn5 ω n 6 \omega_n^6 ωn6 ω n 7 \omega_n^7 ωn7
第一轮后: ω n 0 \omega_n^0 ωn0 ω n 2 \omega_n^2 ωn2 ω n 4 \omega_n^4 ωn4 ω n 6 \omega_n^6 ωn6| ω n 1 \omega_n^1 ωn1 ω n 3 \omega_n^3 ωn3 ω n 7 \omega_n^7 ωn7 ω n 5 \omega_n^5 ωn5
第二轮后: ω n 0 \omega_n^0 ωn0 ω n 4 \omega_n^4 ωn4| ω n 2 \omega_n^2 ωn2 ω n 6 \omega_n^6 ωn6| ω n 1 \omega_n^1 ωn1 ω n 5 \omega_n^5 ωn5| ω n 3 \omega_n^3 ωn3 ω n 7 \omega_n^7 ωn7
第三轮后: ω n 0 \omega_n^0 ωn0| ω n 4 \omega_n^4 ωn4| ω n 2 \omega_n^2 ωn2| ω n 6 \omega_n^6 ωn6| ω n 1 \omega_n^1 ωn1| ω n 5 \omega_n^5 ωn5| ω n 3 \omega_n^3 ωn3| ω n 7 \omega_n^7 ωn7
“|”代表分组界限
把每个位置用二进制表现出来。位置x上的数,最后所在的位置是“x二进制翻转得到的数”,例如4(100)最后到了1(001)5(101)最后不变为5(101),3(011)最后到了6(110)。
所以我们先把每个数放到最后的位置上,然后不断向上还原,同时求出点值表示就可以啦。
迭代版FFT就比之前的递归版快多了,真√ O ( n l o g 2 n ) O(nlog_2n) O(nlog2n)绝妙算法
代码实现FFT
下面是本人写的FFT加速高精度乘法的代码(并有详细注释):
#include<bits/stdc++.h>
using namespace std;
//complex是stl自带的定义复数的容器
typedef complex<double> cp;
#define N 2097153
//pie表示圆周率π
const double pie=acos(-1);
int n;
cp a[N],b[N];
int rev[N],ans[N];
char s1[N],s2[N];
//读入优化
int read(){
int sum=0,f=1;
char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){sum=(sum<<3)+(sum<<1)+ch-'0';ch=getchar();}
return sum*f;
}
//初始化每个位置最终到达的位置
{
int len=1<<k;
for(int i=0;i<len;i++)
rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));
}
//a表示要操作的系数,n表示序列长度
//若flag为1,则表示FFT,为-1则为IFFT(需要求倒数)
void fft(cp *a,int n,int flag){
for(int i=0;i<n;i++)
{
//i小于rev[i]时才交换,防止同一个元素交换两次,回到它原来的位置。
if(i<rev[i])swap(a[i],a[rev[i]]);
}
for(int h=1;h<n;h*=2)//h是准备合并序列的长度的二分之一
{
cp wn=exp(cp(0,flag*pie/h));//求单位根w_n^1
for(int j=0;j<n;j+=h*2)//j表示合并到了哪一位
{
cp w(1,0);
for(int k=j;k<j+h;k++)//只扫左半部分,得到右半部分的答案
{
cp x=a[k];
cp y=w*a[k+h];
a[k]=x+y; //这两步是蝴蝶变换
a[k+h]=x-y;
w*=wn; //求w_n^k
}
}
}
//判断是否是FFT还是IFFT
if(flag==-1)
for(int i=0;i<n;i++)
a[i]/=n;
}
int main(){
n=read();
scanf("%s%s",s1,s2);
//读入的数的每一位看成多项式的一项,保存在复数的实部
for(int i=0;i<n;i++)a[i]=(double)(s1[n-i-1]-'0');
for(int i=0;i<n;i++)b[i]=(double)(s2[n-i-1]-'0');
//k表示转化成二进制的位数
int k=1,s=2;
while((1<<k)<2*n-1)k++,s<<=1;
init(k);
//FFT 把a的系数表示转化为点值表示
fft(a,s,1);
//FFT 把b的系数表示转化为点值表示
fft(b,s,1);
//FFT 两个多项式的点值表示相乘
for(int i=0;i<s;i++)
a[i]*=b[i];
//IFFT 把这个点值表示转化为系数表示
fft(a,s,-1);
//保存答案的每一位(注意进位)
for(int i=0;i<s;i++)
{
//取实数四舍五入,此时虚数部分应当为0或由于浮点误差接近0
ans[i]+=(int)(a[i].real()+0.5);
ans[i+1]+=ans[i]/10;
ans[i]%=10;
}
while(!ans[s]&&s>-1)s--;
if(s==-1)printf("0");
else
for(int i=s;i>=0;i--)
printf("%d",ans[i]);
return 0;
}
后记
这篇博客写了一天,终于写完了,完结撒花✿✿ヽ(°▽°)ノ✿
FWT我来啦!!!